Ampere's Circuital Law

Ampere's Circuital Law, named after the French mathematician and scientist Andr�-Marie Ampere, is a fundamental principle in electromagnetism. The law outlines the link between a current-carrying wire's magnetic field and the current itself. It is one of the four Maxwell equations that serve as the foundation of classical electromagnetic theory.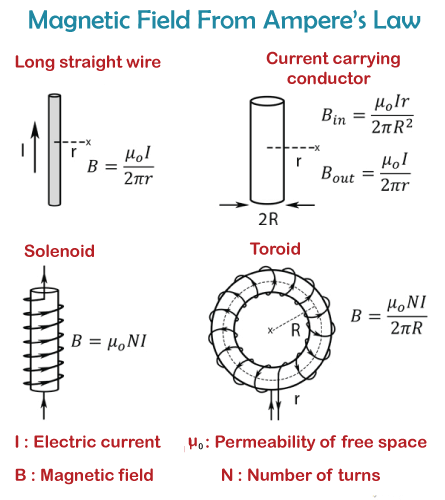

Ampere's law states, in essence, that the magnetic field around a closed loop of wire is proportional to the electric current running through the loop. This law is very important in understanding the behavior of magnetic fields generated by electric currents, and it has a wide range of practical applications in domains such as electrical engineering, electronics, and telecommunications.

The behaviour of the magnetic field formed by a current-carrying wire can be used to explain the idea behind Ampere's law. The magnetic field is made up of force lines that encircle the wire and run perpendicular to the direction of current flow. These lines of force form circular loops around the wire, with the magnetic field's direction determined by the right-hand rule. The magnetic field's magnitude varies with the current flowing through the wire and the distance from the wire.

According to Ampere's law, the total magnetic field around a closed loop of wire is equal to the sum of all currents going through the loop. The following is a mathematical expression for the law:

∫B.dl = μ₀I

Where, B.dl is the line integral of the magnetic field around the closed loop,

I is the total current going through the loop, and

μ₀ is the permeability of empty space, which is a constant of about 4 x 10^-7 N/A².

The sum of the dot products of the magnetic field and the differential length elements along the closed loop is represented by the line integral. This signifies that the integral assesses the magnetic field component along the line element's direction. The line element's direction is assumed to be along the tangent of the closed loop, i.e., it follows the course of the current around the loop.

Ampere's law's mathematical expression can be used to compute the magnetic field at a certain position around a current-carrying wire. For example, if we consider a long straight wire carrying a current I, we can determine the magnetic field at a point P at a distance r from the wire using the formula:

B = μ₀I/(2πr).

This formula shows that the magnetic field is inversely proportional to the distance from the wire and directly proportional to the current. It also demonstrates the inverse-square law, which states that the magnetic field diminishes with distance from the wire.

Ampere's law can also be applied to more sophisticated current-carrying wire systems. The closed loop utilised in the line integral in this case could be a path that encloses numerous wires. The sum of the currents flowing through each wire results in the overall current flowing through the loop. Using the above method, the magnetic field at any location around the loop may be computed by adding the contributions from each wire.

Why Ampere Circuital Law is Important?

• One of Ampere's most important resu is that it allows us to predict the behaviour of magnetic fields in the presence of changing electric fields. This is due to the fact that electric fields can induce currents in conductive materials, which generate magnetic fields. The magnetic field around a closed loop is proportional to the current running through the loop, and this current can be produced by a changing electric field, according to Ampere's equation.
• Ampere's law is also useful in the design and operation of electric motors and generators. Magnetic fields are used in these devices to convert electrical energy into mechanical energy (motors) or vice versa (generators). Current-carrying wire coils generate the magnetic field, and Ampere's law can be used to calculate the strength and distribution of the magnetic field surrounding the coils. This information is crucial for optimising the device's efficiency and performance.
• Ampere's law is also important in understanding superconductor behaviour. When cooled below a particular temperature, superconductors may conduct electricity with zero resistance. When a current travels through a superconductor, it produces a magnetic field that can be many times stronger than the magnetic field produced by a regular wire. Ampere's law describes this effect, which is known as the Meissner effect.
• Ampere's law has played a major part in the development of contemporary physics, in addition to its practical uses. Ampere developed the law in the early nineteenth century, and it was critical in the development of the science of electromagnetic. It was then added into Maxwell's equations, which linked the fields of electricity and magnetism, paving the way for the creation of electromagnetism theory.
• Ampere's law is also important in the study of more exotic phenomena in physics, such as black holes and cosmic strings. The law is utilised in various circumstances to compute the magnetic fields and electric currents surrounding these items, which can then provide insights into their properties and behaviour.

This interaction of electric and magnetic fields is important to electromagnetic radiation such as radio waves and light. These waves are created by accelerating charges, which produce shifting electric and magnetic fields that travel over space. The behaviour of these waves and their interactions with matter are described by Maxwell's equations, which include Ampere's law.

Ampere's law is very strongly related to Faraday's law of electromagnetic induction, another fundamental principle in electromagnetism. According to Faraday's law, a changing magnetic field can create an electromotive force (EMF) in a conductor. This EMF can then cause a current to flow through the conductor, producing a magnetic field that opposes the original magnetic field change. Faraday's law is an important idea in the design of electrical generators and transformers, both of which employ magnetic fields and changing currents to convert electrical energy from one form to another.

The Maxwell-Faraday equation, which describes how a changing magnetic field can generate a circulating electric field, connects Ampere's law and Faraday's law. This equation, together with the other three Maxwell's equations, describes the behaviour of electric and magnetic fields and their interactions with matter in detail.

Ampere's Circuital Law is a fundamental principle in electromagnetism with numerous applications in science and technology. It is significant not just for its practical value, but also for its contribution to the advancement of contemporary physics and our knowledge of the fundamental nature of the cosmos.

Conclusion

Ampere's Circuital Law, in conclusion, is a fundamental principle in electromagnetism that outlines the link between electric currents and magnetic fields. The law is employed in a variety of applications, including electric motors and generators, superconductors, and electromagnetic radiation. Understanding the ideas underlying Ampere's law is critical for anyone working in the fields of electrical engineering, electronics, or physics since it provides a strong tool for problem-solving and the invention of new technologies.