Circular Motion

Introduction:

In physics, if a particle shows movement such that the motion traces the circumference of a circle then such motion is described as Circular Motion.

Circular motion can either be uniform or Non-uniform in nature.
Whether the circular motion is uniform or non-uniform is dictated by the angular speed. If the angular speed and the rate of angular rotation is constant then the circular motion is described as Uniform circular motion and if the angular speed and rate of angular rotation are not constant then the circular motion is said to be Non-uniform circular motion.

Some simple examples of circular motion are:

• The moon's rotation around the earth
• The spinning of a tire
• The rotation of blades of a ceiling fan
• The motion of a windmill.

Variables:

Similar to linear motion, circular motion also contains a set of variables that define the characteristics of the motion. These are namely: Angular displacement, Angular velocity and Angular acceleration.

1. Angular Displacement (θ):

Angular displacement can be described as the change in the position of an object in a circular motion with respect to time. In more specific terms, it is the rate at which an object changes its position angularly with respect to time. It is represented as theta (θ). It is measured in Radians.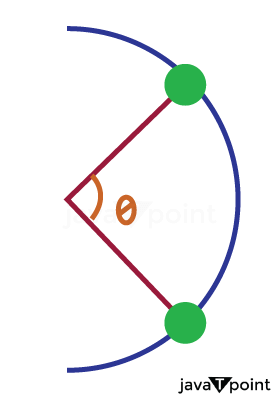

2. Angular Velocity (⍵):

Angular velocity is termed the rate at which an object in circular motion changes its angular displacement. In simpler words, it can be determined as the speed at which an object in angular motion can change its position. It is denoted by omega (⍵). The unit in which angular velocity is measured is radians per second or rad/sec or rad s-1. Mathematically, it can be described as:

⍵ = 𝚫θ / t

here,

⍵ represents the angular velocity

𝚫θ represents the change in angular displacement

t represents the time taken for the change in angular displacement to occur

Angular speed can be defined as the magnitude of the angular velocity.

3. Angular Acceleration (⍺):

The angular acceleration of an object depicting circular motion can be explained as the rate at which the object changes its angular velocity. In other words, it is the change in the angular velocity of an object with respect to time. To understand it better, in easier words, it can be called the measure of how much speed an object changes in a given time frame. It is denoted by the symbol Alpha (⍺). It is measured in the unit radians per second squared or rad / s-2. Mathematically it can be defined as:

⍺ = 𝚫⍵ / t

here,

⍺ represents the angular acceleration

𝚫⍵ denotes the change in angular velocity over a period of time t

t represents the time taken for the change in angular velocity to occur.

In circular motion, the acceleration of the object has 2 components namely angular acceleration and tangential acceleration (a_t). The tangential acceleration works tangentially outwards with respect to the path of motion of the object.

a_t = 𝚫v / t

Here,

v depicts the linear velocity of the object.

Note: For uniform motion, the tangential acceleration is zero

These two variables, angular velocity and angular acceleration, dictate whether the circular motion of an object will be Uniform or non-uniform. If the angular velocity and the angular acceleration of an object are constant then the motion is said to be uniform circular motion. However, if the angular acceleration of an object is not constant then the circular motion is said to be Non-Uniform.

Relation with Linear Variables:

When written in vector form, we can obtain relations between the linear and angular variables:

Angular velocity: The product of the radius (position) vector (r) and the angular velocity of the object is equal to the linear velocity (v) of the object.

v = r⍵

Angular acceleration: The product of the radius (position) vector (r) and the angular acceleration of the object is equal to the linear acceleration (a) of the object.

a = r⍺

Forces associated with an Object Depicting Circular Motion:

1. Moment of Inertia (I):

Similar to inertia in linear momentum, the moment of inertia in circular motion also refers to the tendency of any object to resist or oppose the change in the state of its circular motion. The moment of inertia of any object depicting circular motion is governed by the distribution of the mass and the shape of the object. It is denoted by capital 'i' (I). The moment of inertia is a scalar quantity, meaning that it has magnitude but no direction. Kilogram meter squared (k*m²) is the S.I unit of moment of inertia.

The mathematical representation of the moment of inertia of a point mass rotating in a circular path around a fixed axis is given by:

I = m*r²

where:

'I' is the moment of inertia.

'm' represents the mass of the point object.

'r' is the perpendicular distance from the axis of rotation to the point mass.

Moment of inertia in daily life:

• The moment of inertia determines where and how fast a spinning top will tip over.
• The moment of inertia of the tires of the car determines how fast or easily will the car accelerate or decelerate.
• The moment of inertia of a dancer determines how fast they can spin, they can reduce or increase the speed of their spinning by changing their distribution of mass.

2. Angular Momentum (L):

For any object, having mass m, moving in a circular motion there exists a linear momentum (p) which is equal to the product of the linear velocity (v) and the mass of the object

p = mv

Along with linear momentum, there will also be angular momentum (L) at a point in time (t). This angular momentum is defined as the product of the linear momentum (p) and the radius (or position) vector r:

L= r p

Angular momentum is a vector quantity, meaning it has both magnitude and direction.

When there are no external forces working on the object while it is performing circular motion, the angular momentum of the object remains unchanged or constant. This phenomenon is known as the conservation of angular momentum. Conservation of momentum is a very crucial term in physics as it offers an explanation for the behavior of a large number of objects in a circular motion. For example, the change in the spinning speed of a dancer when they fold and unfold their arms.

3. Centripetal Force:

In circular motion, an object follows a circular path however, according to Newton's 1st law an object should follow a straight path until and unless an external force is applied to it. For an object moving in a circular path, this external force is termed a Centripetal force.

Centripetal Force can be said to be the force that causes the object to follow a path that is curved. The centripetal force is always directed radially inwards to the path followed by the object. Centripetal force isn't a new type of fundamental force, in reality, it is just the name given to describe the net force acting on an object in a circular motion.

Since Centripetal force is also a force, the S.I. unit for centripetal force is Newton (N)

The angular acceleration of an object moving in a circular motion can be written as

⍺= v2/r or (4 π2 r)/T

For an object in circular motion, the force acting on it is directed radially inwards and is known as centripetal force. Using Newton's 2nd law we can obtain the relation:

F=m*a (for linear momentum)

F= m*⍺ (for angular momentum)

F= m*v²/r

F=m(4 π² r)/T

Examples of Centripetal Force:

• As the Earth revolves around the sun in its orbit, it experiences a centripetal force.
• A car turning or driving through a roundabout experiences centripetal force.
• A ball attached to a string when spun around, experiences centripetal force.

4. Centrifugal Force:

Centrifugal force can be described as a pseudo force or a fictitious force or an inertial force. What this means is that it is observed from a non-inertial frame of reference or a rotating frame of reference, meaning that this force is not considered when we are in an inertial frame of reference. This force acts radially outwards on an object in circular motion.

Centrifugal force is further justified by Newton's third law of motion which states that every action must have an equal reaction in opposition to the said action, therefore to counteract the centripetal force, there must be a force that acts in the opposite direction, which is centrifugal force.

Centrifugal force has the same dimensions and magnitude as the centripetal force. The way it does differ from the centripetal force is that it works radially outwards on the object whereas the centripetal force works radially inwards, i.e., in the opposite direction.

Since it is the same as a centripetal force but in the opposite direction, its mathematical formula can be depicted as:

F = (m*v²)/r

or

F = m*⍵²*r

This force is extremely useful, especially in practical applications such as separating liquids in a centrifuge.

As it is a force the S.I. unit of centrifugal force is also Newton (N).

Examples of Centrifugal Forces:

• When you ride a car or any vehicle and it takes a sharp turn, you feel a "push" to the opposite side of the direction of turning, this is because of centrifugal force.
• The clothes in a washing machine tend to stick to the edges of the drum, this is the result of the centrifugal force.

Centrifugal force is often referred to as a 'perceived' force as it is not necessarily a force but a result of inertia.

Difference between Centripetal and Centrifugal Force:

• The first major difference is in the frame of reference in which they are both observed and measured. Centripetal force is measured in an inertial frame of reference whereas centrifugal force is measured in a rotational or non-inertial frame of reference.
• A second difference is the direction of functioning of the two forces. Centripetal force is directed radially inwards, perpendicular to the axis of rotation. Centrifugal force is directed radially outwards, i.e., in the opposite direction of the centripetal force.

Note: Neither the Centripetal force nor the centrifugal force are fundamental forces. Centripetal force is just a method of referring to the net force which draws the object towards the center and prevents it from undergoing linear motion. This net force could be gravitational force for celestial bodies, tension for a ball attached to a thread or a string and for a car turning it can be the friction of the wheels. All these forces pull the object towards the axis of rotation.

In comparison to this, centrifugal force can be called a 'perception' of a force as it is not really a force but an effect caused by the moment of inertia. The push passengers feel towards the outwards direction when the vehicle turns is the perfect example of this 'perceptive' force.

5. Torque (τ):

Torque can be described as a force which causes a turning effect about the axis of rotation of an object in a circular motion. In simpler words, it is a force which causes the object to turn or twist. Mathematically it can be defined as the cross-product of the centripetal force and the position vector which is perpendicular to the axis of rotation of the object at a certain point in time:

τ = r x F

τ = r FSinθ

If the angular momentum of an object is constant then the torque acting on the said object is zero.

The S.I unit of Torque is N m or Newton meter.

Example:

• When a force is applied to the door handles, that force causes the door to rotate around its hinges and hence the door opens. This force applied exerts torque.
• Using a wrench to tighten or loosen bolts involves applying torque. By applying a force perpendicular to the wrench handle, a torque is applied to the screws which causes them to turn and come out or go in.
• Opening a lid of a jar also involves torque. When you apply force to twist open the lid of the jar, you are applying torque to the lid. This causes the lid to twist and turn and eventually open.

Afterword:

The aforementioned forces are the forces that work on an object that is moving in a circular motion. These forces apply to small objects and particles (friction, tension etc.) as well as to celestial bodies such as planets and stars (gravitational forces). However it must be noted that these forces and their magnitudes are measured in simple circular motion, as the motion of the object becomes more complex, the forces applied to it and their direction as well as their magnitudes also start to differ.