Strain Energy

Strain energy is a concept in mechanics that describes the potential energy stored in an object as a result of deformation or strain. It is a fundamental principle that underlies many engineering applications, from the design of bridges and buildings to the analysis of materials and structures. In this article, we will explore the concept of strain energy in more detail, including its definition, calculation, and significance in various fields of engineering.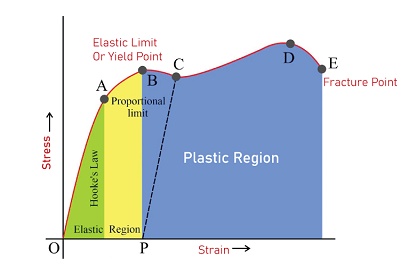

The amount of strain energy stored in an object depends on several factors, including the magnitude of the applied force, the type of material the object is made of, and the degree of deformation or strain. The equation for calculating strain energy is:

Strain energy = 1/2 x Force x Deformation

Where Force is the applied force, and Deformation is the degree of deformation or strain.

Strain Energy Equation

The equation for strain energy can be derived from the work-energy principle. According to this principle, the work done on an object is equal to the change in its kinetic and potential energy. In the case of an object that undergoes deformation, the work done on the object is stored as potential energy, which is known as strain energy.

Consider an object that is subjected to an external force F. As a result of this force, the object undergoes deformation, and its length changes from L to L + ΔL. The work done by the external force on the object is given by the equation:

W = FΔL

This work done is stored as potential energy in the object in the form of strain energy. The strain energy U is given by the equation:

U = W = FΔL

This equation provides the basic framework for the derivation of strain energy.

Strain Energy Density Equation:

The strain energy density equation is a more specific form of the strain energy equation that is used to calculate the amount of strain energy stored per unit volume of material. To derive this equation, we start with the equation for strain energy:

U = FΔL

We can rewrite this equation as:

U = F x (ΔL/L) x L

where (ΔL/L) is the strain in the object.

Dividing both sides of the equation by the volume of the object V gives:

U/V = F x (ΔL/L) x (L/V)

where (L/V) is the strain in the material.

Since stress (σ) is defined as the force per unit area, we can write F/A as σ. Similarly, strain (ε) is defined as the change in length per unit length, so we can write (ΔL/L) as ε. Substituting these values into the equation gives:

U/V = σ x ε x (L/2L)

Solving for U/V, we get:

U/V = 1/2 x σ x ε

This equation is known as the strain energy density equation and is used to calculate the amount of strain energy stored per unit volume of material.

Strain Energy in a Spring

One of the most common examples of strain energy is the deformation of a spring. When a spring is compressed or stretched, it stores potential energy in the form of strain energy. To derive the equation for strain energy in a spring, we start with the equation for the strain energy of an object:

U = FΔL

In the case of a spring, the force F is given by Hooke's Law:

F = kΔL/2

where k is the spring constant and ΔL is the deformation of the spring.

Substituting F into the equation for strain energy, we get:

U = kΔL²/2

This equation provides the specific form of the strain energy equation for a spring.

Types of Strain Energy

There are different types of strain energy, depending on the nature of the deformation and the type of load applied to the material. In this article, we will discuss the various types of strain energy in detail.

Tensile strain: Energy Tensile strain energy is stored in a material when subjected to tensile or stretching forces. When a material is pulled or stretched, the molecules within it are pulled apart, causing the material to deform. The energy required to stretch the material is stored in the form of tensile strain energy. The amount of tensile strain energy stored in a material is directly proportional to the amount of deformation it undergoes.

Compressive strain energy: Compressive strain energy is stored in a material when subjected to compressive forces. When a material is compressed, the molecules within it are pushed closer together, causing the material to deform. The energy required to compress the material is stored in the form of compressive strain energy. The amount of compressive strain energy stored in a material is directly proportional to the amount of deformation it undergoes.

Shear strain: Energy Shear strain energy is stored in a material when subjected to shear forces. When a material is subjected to a shear force, the molecules within it are displaced parallel to the applied force, causing the material to deform. The energy required to shear the material is stored in the form of shear strain energy. The amount of shear strain energy stored in a material is directly proportional to the amount of deformation it undergoes.

Bending strain: Energy Bending strain energy is stored in a material when subjected to bending or flexural forces. When a material is bent, the molecules within it are displaced perpendicular to the applied force, causing the material to deform. The energy required to bend the material is stored in the form of bending strain energy. The amount of bending strain energy stored in a material is directly proportional to the amount of deformation it undergoes.

Torsional strain energy: Torsional strain energy is stored in a material when subjected to torsional or twisting forces. When a material is twisted, the molecules within it are displaced in a circular motion around the applied force, causing the material to deform. The energy required to twist the material is stored in the form of torsional strain energy. The amount of torsional strain energy stored in a material is directly proportional to the amount of deformation it undergoes.

Thermal strain energy: Thermal strain energy is the energy stored in a material when it is subjected to changes in temperature. When a material is exposed to changes in temperature, it expands or contracts, causing the material to deform. The energy required to deform the material due to changes in temperature is stored in the form of thermal strain energy. The amount of thermal strain energy stored in a material is directly proportional to the amount of deformation it undergoes.

Residual strain energy: Residual strain energy is the energy stored in a material when it undergoes permanent deformation. When a material is subjected to excessive deformation, it may undergo permanent deformation, meaning that it does not return to its original shape after the load is removed. The energy required to cause permanent deformation in a material is stored in the form of residual strain energy. The amount of residual strain energy stored in a material is proportional to the amount of permanent deformation it undergoes.

Fatigue strain energy: Fatigue strain energy is stored in a material when subjected to cyclic loading. When a material is subjected to cyclic loading, it undergoes repeated cycles of deformation and relaxation, causing it to undergo fatigue failure. The energy required to cause fatigue failure in a material is stored in the form of fatigue strain energy. The amount of fatigue strain energy stored in a material is proportional to the number of loading cycles it undergoes.

Creep strain energy: Creep strain energy is the energy stored in a material when it undergoes creep deformation. Creep deformation is a material's gradual and time-dependent deformation under a constant load or stress. The energy required to cause creep deformation in a material is stored in the form of creep strain energy. The amount of creep strain energy stored in a material is proportional to the duration and magnitude of the applied load or stress.

Hydrostatic strain energy: Hydrostatic strain energy is stored in a material when subjected to hydrostatic pressure. Hydrostatic pressure is the pressure exerted by a fluid that is in equilibrium and acts equally in all directions. When a material is subjected to hydrostatic pressure, it undergoes uniform deformation, and the energy required to cause this deformation is stored in the form of hydrostatic strain energy.

Application of Strain Energy

Strain energy is a type of potential energy stored within an object or material as a result of deformation or strain. It is a fundamental concept in physics, engineering, and materials science, and it has a wide range of applications across various industries. In this article, we will discuss the applications of strain energy in detail.

Mechanical Engineering

Mechanical engineering is one of the primary fields where strain energy finds extensive use. One of the most common applications of strain energy in mechanical engineering is in the design of springs. Springs are used in a wide range of mechanical systems, including watches, cars, and machines. The potential energy stored within a spring as it is compressed or stretched is a form of strain energy. When the spring is released, this potential energy is converted into kinetic energy, which can be used to perform work or power machines.

Another application of strain energy in mechanical engineering is in the design of shock absorbers. Shock absorbers are used to dampen the effects of vibrations and shocks in mechanical systems. They work by converting the kinetic energy of the system into strain energy, which is then dissipated as heat. The design of shock absorbers is based on the principle of Hooke's Law, which states that the force required to compress or stretch a spring is proportional to the displacement of the spring.

In addition to springs and shock absorbers, strain energy is also used in the design of other mechanical components, such as bearings, gears, and camshafts. These components are designed to withstand various types of loads, including torsion, compression, and tension. Strain energy is used to ensure that the potential energy stored within these components is sufficient to resist deformation and failure under these loads.

Civil Engineering

Civil engineering is another field where strain energy finds extensive use. In civil engineering, strain energy is used to design and analyze various types of structures, including bridges, buildings, and tunnels. Structures are subjected to various types of loads, including dead loads, live loads, wind loads, and seismic loads. Strain energy is used to design these structures to withstand these loads by ensuring that the potential energy stored within the structure is sufficient to resist deformation and failure.

For example, in the design of a bridge, strain energy is used to ensure that the bridge can withstand the weight of traffic passing over it without collapsing or deforming. The potential energy stored within the bridge structure as it is loaded with traffic is a form of strain energy. By analyzing the amount of strain energy stored within the structure, engineers can determine the strength and stability of the bridge.

Materials Science

Materials science is another field where strain energy finds extensive use. In materials science, strain energy is used to understand the behavior of materials under different types of stress. By measuring the amount of strain energy stored within a material, scientists can determine its elastic modulus, which is a measure of the material's stiffness.

One of the most common applications of strain energy in materials science is in the testing of materials. Materials are subjected to various types of stress, including tension, compression, and torsion, to determine their strength and deformation behavior. Strain energy is used to measure the amount of deformation that occurs within the material as it is subjected to stress. This information is then used to determine the material's mechanical properties, including its strength, stiffness, and ductility.

Biomechanics

Biomechanics is the study of the mechanics of biological systems, including the human body. Strain energy is used in biomechanics to understand the deformation behavior of biological tissues, such as bone, cartilage, and muscle. By measuring the amount of strain energy stored within these tissues, scientists can determine their mechanical properties and their response to different types of stress.

For example, in the design of orthopedic implants, strain energy is used to ensure that the implant can withstand the stresses and strains of the human body. Implants, such as hip replacements, are subjected to various types of loads, including compression, tension, and torsion. Strain energy is used to design these implants to ensure that they have the necessary strength and durability to withstand these loads without deformation or failure.

Another application of strain energy in biomechanics is in the study of muscle mechanics. Muscles are responsible for generating force and movement in the body. They are made up of bundles of muscle fibers that contract and elongate in response to electrical impulses from the nervous system. Strain energy is used to understand the mechanical behavior of muscle fibers, including their elasticity, stiffness, and strength.

Energy Storage

Strain energy is also used for energy storage in various systems, including flywheels and compressed air energy storage systems. Flywheels store energy by spinning a heavy rotor at high speeds, which creates a significant amount of strain energy. When the energy is required, the rotor is slowed down, and the stored energy is released. Compressed air energy storage systems store energy by compressing air in a container, which creates a significant amount of strain energy. When the energy is required, the compressed air is released, which can be used to power turbines and generate electricity.