Angular Velocity

The idea of angular velocity in physics refers to the speed at which an item spins or revolves around a fixed axis. In other words, it calculates the rate of rotation of an object about a given point. It is a key idea in the study of rotational motion and has many uses in astronomy, engineering, and other disciplines. The Greek letter omega (ω) is commonly used to represent angular velocity. It is described as the rate of variation in angle over a given period of time for an item. The following formula gives the angular velocity in mathematics:

ω = dθ/dt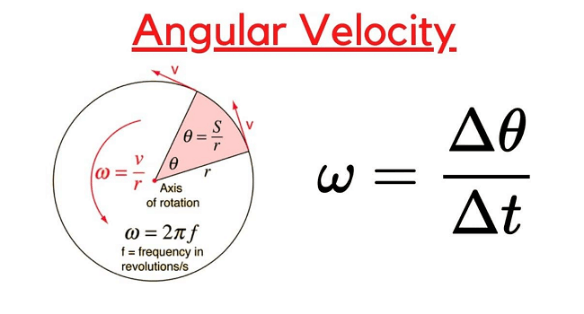

Where,

t is the passage of time,

ω is the angular velocity,

and θ is the angle through which the object has rotated.

Although it can alternatively be represented in degrees per second (deg/s), angular velocity is measured in radians per second (rad/s). The fact that angular velocity is a vector quantity, meaning it has both magnitude and direction, is one of its important characteristics. The angular velocity vector has a direction that is right-handed and perpendicular to the plane of rotation. In other words, your thumb points in the direction of the angular velocity vector if the fingers of your right-hand curl in the direction of rotation.

The study of rotational dynamics is one of the most significant areas in which angular velocity is applied. The forces that drive objects to spin and how they impact an object's motion are the subject of this study. The torque equation, which connects the net torque exerted on an object to its angular acceleration, is one of the fundamental equations in rotational dynamics:

τ = Iα

where,

I, which is a measure of an item's resistance to rotational motion, is the moment of inertia,

α is the angular acceleration, and

τ is the net torque acting on the object.

This equation, which is used to resolve issues with rotational motion and forces, is comparable to Newton's second law of motion (F=ma) in linear motion.

Rigid Body Motion

In the study of rigid body motion, which is the motion of an object that keeps its size and shape while it moves, angular velocity is also crucial. Angular velocity is used to describe both the motion of the item as a whole and the motion of its individual components in this context. In the study of rotating machinery, such as engines and turbines, where the rotation of many elements must be meticulously controlled and observed, it is particularly crucial.

Angular Velocity in Astronomy

Angular velocity is a term used in astronomy to describe the motion of celestial bodies like planets and stars. For instance, the length of a day is determined by the angular velocity of the Earth as it rotates around its axis, while the length of a lunar month is determined by the angular velocity of the Moon as it orbits the Earth.

Importance of Angular Velocity

A key idea in physics, angular velocity has several applications in the domains of engineering, mechanics, and astronomy. Among the main factors angular velocity is significant are:

• Understanding Rotational Motion

The study of rotational motion is based on angular velocity. It gives us a way to quantify the rate of change of an object's rotational motion and to define how quickly an object is spinning around a fixed axis. Understanding phenomena like the stability of spinning systems and the behavior of moving objects depends on this.

• Engineering and Mechanics

The concept of angular velocity is crucial in both fields. It is applied to the study of mechanical motion in turbines, engines, and generators. For instance, in order to guarantee that an engine operates effectively and does not sustain excessive wear and tear, the angular velocity of the rotating parts must be carefully managed.

• Astronomy and Astrophysics

Angular velocity is significant in both fields. It is used to explain how celestial bodies like planets, moons, and stars move. For instance, the length of a day is determined by the angular velocity of the Earth's rotation, whereas the length of a lunar month is determined by the angular velocity of the Moon's orbit.

Conclusion

In summary, the term "angular velocity" refers to the rate at which an object spins around a fixed axis in physics. It is a magnitude-and-direction-dependent vector quantity that is strongly related to angular acceleration and other rotational dynamics ideas. Angular velocity is a crucial tool for comprehending the motion of objects in a variety of disciplines, including engineering, astronomy, and others.