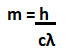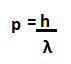Quantum Physics

Quantum physics is a branch of physics that is the study of matter and energy. The matter is composed of a large number of oscillating particles, which vibrate with different frequencies. These particles of the matter and have any value of frequency and vibrations.

Energy comes in the form of packets called quanta. These packets cannot be divided further into components. Thus, quantum physics is a modern physical that is based on theoretical concepts.

Quantum physics and Quantum Mechanics

Quantum mechanics was developed from the basics of Quantum physics. Quantum physics is a study of particles and matter at the atomic level, while Quantum mechanics is the study of particles and matter at a more specific level. We can also say that it is the study at the subatomic level.

Let's discuss the development of Quantum physics and Quantum mechanics.

In the early, Quantum physics and its laws were unable to follow the classical mechanic's laws. Hence, it was named Quantum theory. It is the theoretical approach rather than the practical one. Hence, we can say that Quantum physics is generally called Quantum theory.

Around the 1920s, mathematical laws were developed by the physicist that described the Quantum theory. After the development of such laws, physicists called it Quantum mechanics or classical mechanics.

Thus, we can say that Quantum physics is similar to Quantum mechanics. The difference lies in the theory and the mathematical calculations.

Here, we will generally discuss the Quantum theory, which refers to the theoretical Quantum mechanics. The topics discussed in this topic are as follows:

History

Black Body

Quantum theory of Radiations

Uncertainty Principle

Schrödinger Equation

Symmetry

Quantum States

Dirac Equation

Properties of Photons

Collision between photon and Matter particle

Photoelectric Effect

Long Wavelength

Kinetic Energy of Photoelectrons

Types of Photoelectric cell

History

• The discovery of cathode rays by Michael Faraday in 1838 led to the development of the statement of black-body radiation.
• The Quantum theory was proposed by Max Planck (German physicist) around 1900 when he was trying to discover the shape of the black body radiation curve.
• Einstein extended the Quantum theory around 1905. It covered all the radiations, including light rays and Gamma rays.
• At the end of the 117th century, a Corpuscular theory was developed by Newton. According to the theory, light consists of a stream of invisible fast-moving particles called corpuscles.
• Around 1864, the theory was followed by Maxwell's electromagnetic theory. According to the Maxwell theory, light consists of electric and magnetic stress changes that originated in the motion of the electricity.
• Quantum physics was further modified in modern times to Quantum mechanics.
• Around the 1920s, Quantum mechanics became the standard formulation of atomic physics.
• It comprises various disciplines, such as Quantum chemistry, Quantum electronics, etc. It provides a useful framework for modern technologies. For example, describing chemical bonding and electrons' behavior in the semiconductor and macroscopic phenomenon in superconductors.

Black Body

The black body or surface is a good absorber of heat. It means that it is also a good absorber of heat radiations. The black body defined by the physicist is not a perfect body. It is defined as a body that can absorb the entire wavelengths incident on it. The emitted radiations by the black body are known as black body radiations.

Quantum theory of Radiations

After the development of quantum theory by Max Planck in 1900, Einstein extended the theory around 1905. Planck's study of black body radiations concludes that absorption or emission of thermal energy is not a continuous process. It takes place in discrete forms.

According to the Einstein theory,

• The light energy is emitted by the indivisible amounts of radiant energy called quanta.
• The quanta travel in space in the form of packets or bundles.
• These packets are called photons. It carries a definite amount of energy.

The energy carried by a particular phone is given by:

E = hf

Where,

h is the Planck's constant.

f is the frequency of radiation.

For example,

The photons can be of high frequency or low frequency. The high-frequency photons are those of Gamma rays, while low-frequency photons are of radio waves.

Quantum States

Quantum state is defined as the entity that provides the probability distribution of the outcomes. It is calculated for every possible measurement of the system. The knowledge about Quantum states helps us to predict about the system's behavior.

Quantum states are categorized as pure Quantum states and mixed Quantum states. The pure Quantum states cannot be written as the mixture of other states, while mixed Quantum states can be expressed in the form of other states or mixed states.

Let the 2D vector components be a and b. A pure Quantum state can be expressed as:

|a|^2 + |b|^2 = 1

Where,

|a| and |b| are called as absolute values of a and b.

The probability distribution for various measurements is illustrated by the uncertainty principle. The uncertainty principle illustrates the probability distribution for various measurements. It is a mathematical inequality that can determine certain physical quantities, such as momentum, position, particle, and initial conditions.

The uncertainty principle was introduced in 1927 by the German theoretical physicist Werner Karl Heisenberg.

Schrödinger Equation

The Schrodinger equation describes the position and energy of the electron in space and time. It is defined as a mathematical expression that was named after the Austrian-iris physicist Erwin Schrodinger.

The Schrodinger equation for a single non-realistic in one dimension is represented as: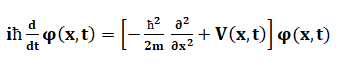

The above equation's wave function assigns a complex number to the point x and each instance of time t.

Here, V(x, t) is the potential, and m is the particle's mass. H is the Planck's constant.

The physical quantities of interest are the operators acting on the Hilbert space. The quantities are position, momentum, and energy.

The time dependent Schrodinger equation is represented as: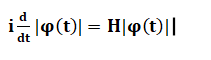

Where,

The Greek letter psi is the state vector.

T is the time.

H is the Hamiltonian operator.

The Hamiltonian operator corresponds to the kinetic energy and potential energy of the system. These two energies together constitute the total energy of the system. The probability density function can be represented as the square of the absolute value of the wave function.

Properties of Photons

Let's discuss some properties of photons.

• Energy
  The energy of a photon is represented by hf. It is different for different kinds of radiation. According to Quantum physics, a photon's energy is always considered an integral multiple of hf.
  Where,
  E = nhf
  But, it is not similar in the case of quantum mechanics. The energy of a photon, according to Quantum mechanics is represented as:
  E = (n + ½) hf
  n anf f are the integer value and the frequency.
  The energy of a photon depends on the frequency of the radiations. It means that the energy of a photon is independent of the intensity.
• Mass of a photon
  The mass energy relation is expressed as:
  E = mc^2
  Where,
  m is the mass of the photon
  c is the speed of the light
  m = E/ c^2
  m = hf / c^2
  We can also write it as:
  
• Momentum of a photon
  The momentum can be expressed as:
  P = mc
  P = hf / c^2
  We can also write it as:
  

The photons are electrically neutral. It means that the photons are not affected under the application of electric and magnetic fields. The methods used to measure the photons' energy or intensity are different from the ordinary method used for other charge carriers.

Collision between photon and Matter particle

The law of conservation of energy applies when the photons collides with the particles of matter. The photons during a collision can disappear or appear, as shown below: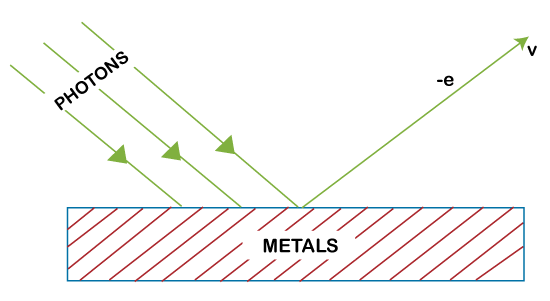

The above figure shows removal or disappearance of photons.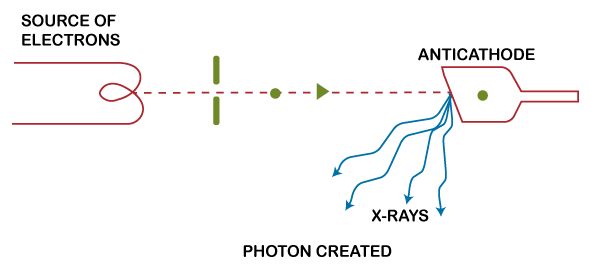

Similarly, the above figure shows the appearance of photons. We can also say that photons can be created or destroyed.

We know that the energy of the photon is given as:

E = hf

Where,

h is the Planck's constant and f is the frequency of radiations.

The kinetic energy lost or gained by the photon is ½ mv^2.

K.E = ½ mv^2

Where,

m is the mass of a particle

v is the velocity

According to the law of conservation of energy,

hf = ½ mv^2

If the material particles carry a charge and are accelerated by the potential difference V, the kinetic energy is eV.

hf = eV

Thus, we can say that:

½ mv^2 = hf = eV

From the above equation, we can easily find out the charged material particle's velocity and the frequency of radiations.

Velocity of the charged material particle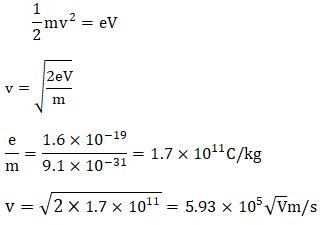

1. Frequency of the emitted radiations

The frequencies of the radiations are emitted when the accelerated charged particle hits the metal surface. The relation can be represented as:

hf = eV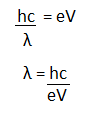

Photoelectric Effect

The photoelectric effect is defined as the process of the ejection of the electrons from a metal surface when radiations or light of a suitable wavelength falls on a metal. The emitted electrons are not different from the usual electrons. The term photoelectron is used to depict electrons' ejection after the fall of radiations on the metal surface.

Long Wavelength

The wavelength corresponding to the threshold frequency is known as the long wavelength. It is represented as: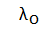

The wavelength of the incident radiations longer than the long wavelength would not be able to eject electrons from the given material. It can be represented as: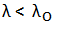

It means that the wavelength of the incident radiations less than the long wavelength can emit electrons from the given material. Such wavelength is also known as threshold wavelength.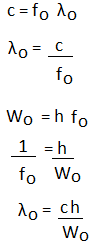

Where,

fo is the threshold frequency. It is defined as the minimum frequency that can cause photoelectric emission.

Wo is the photoelectric work function.

h is the Planck's constant.

c is the speed of light.

Kinetic Energy of Photoelectrons

The Einstein's photoelectric equation can be used to find the velocity and the kinetic energy of the ejected photoelectron.

hf = Wo + ½ mv^2

= hfo + K.E.

K.E. = hf - hfo

K.E. = h (f - fo)

We know that,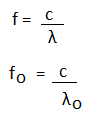

Hence, we can write the above equation as: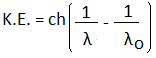

Types of Photoelectric cell

The photoelectric cells convert the light energy to electric energy. The circuit comprises of two electrodes (cathode and anode) and an evacuated glass tube.

The photoelectric cells are categorized as:

• Photo emissive cell
• Photovoltaic cell
• Photoconductive cell

Let's discuss the above three types of cells in detail.

Photoemissive cell

The photoemissive cell consists of two metallic electrodes (cathode and anode) fitted with a base like a thermionic valve, as shown below: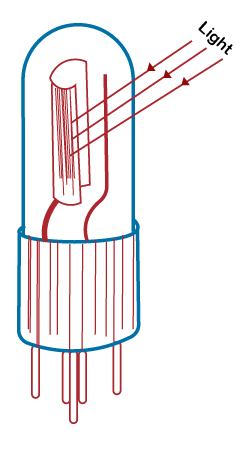

When the cathode is illuminated, the electrons emitted from the cathode are attracted by the positive electrode anode. Thus, the magnitude of the current produced through the flow of electrons depends on the intensity of the incident radiations and anode-to-cathode voltage.

The use of photoemissive cells includes photometry, calorimetry, etc.

Photovoltaic cell

The photovoltaic cell uses a semiconductor contact instead of metals. The incident light causes the generation of internal voltage. It results in the flow of current even if the external battery is not connected to the circuit.

The circuit of the photovoltaic cell is shown below: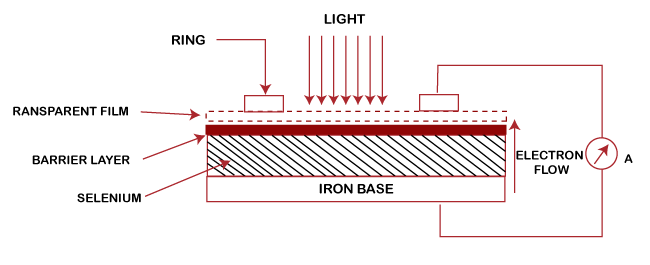

It does not require any external battery for its operation, which is its main advantage. The common photovoltaic cells are the iron selenium cells or Cu-CuO2 cells. The current generated by these cells is large enough to be measured. Hence, it is used in applications, such as portable exposure meters, low resistance relays, etc.

Photoconductive cell

The performance of the photoconductive cell is based on the resistivity of the semiconductor. The simplest form of a photoconductive cell is shown below: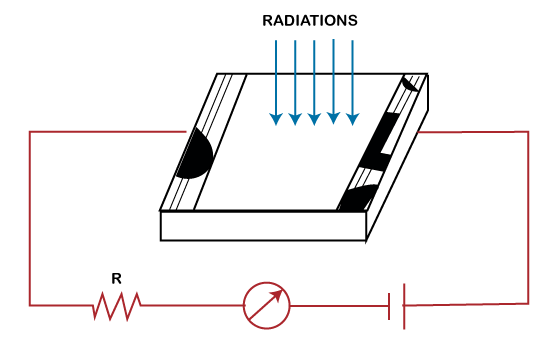

The resistivity decreases when these are irradiated. It means that the semiconductors have low irradiated resistance. The irradiation means the exposure to radiation on the substance.

The commonly used cell is the CdS cell, as shown below: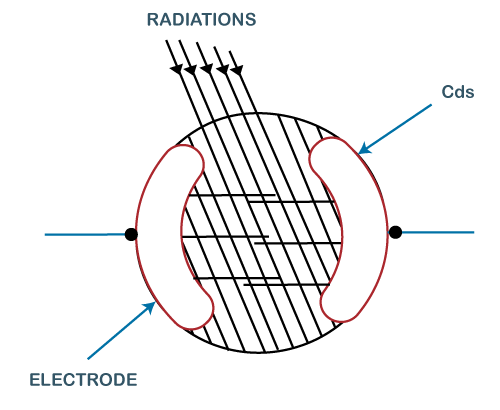

The photoconductive cell comprises the two electrodes and the semiconductor material. When light falls on the cell, its resistance decreases, and the current becomes large. The current becomes small when there is no illumination.

The photoconductive cell is used in applications to detect ships and aircraft, etc.

Applications of Quantum theory

The concept of Quantum theory is the basis for various applications based on our day-to-day life. A common example is the use of computers. The concept of working on a computer is based on Quantum physics.

Other applications include Quantum optics, Quantum chemistry, Quantum computing, optical amplifiers, Superconducting magnets, laser, superconducting magnets, transistors, semiconductors, etc.