Escape Velocity of Earth

Escape velocity is a fundamental concept in physics that represents the minimum velocity required for an object to escape the gravitational pull of a celestial body. In the case of Earth, escape velocity is the speed necessary for an object to overcome Earth's gravitational force and venture into space. This concept has significant implications for space exploration, satellite launches, and understanding the dynamics of our planet. In this article, we will delve into the details of Earth's escape velocity, the factors influencing it, and its practical applications.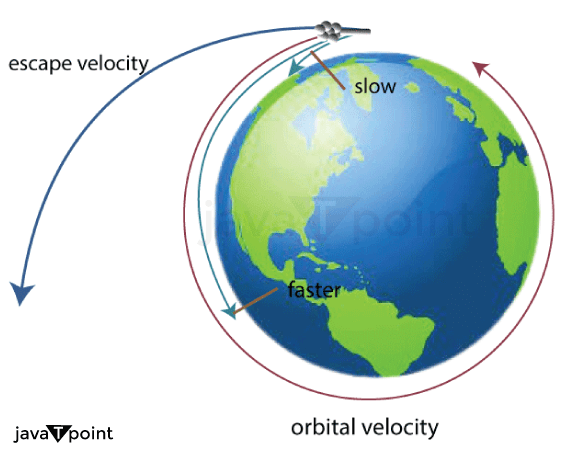

Understanding Escape Velocity

Escape velocity is derived from the concept of gravitational potential energy. Every object near the surface of a celestial body, such as Earth, has gravitational potential energy associated with it. The escape velocity is the amount of kinetic energy required to transform this potential energy into the object's kinetic energy, enabling it to break free from the gravitational pull. In simpler terms, it is the speed needed for an object to "escape" Earth's gravity.

Calculation of Escape Velocity

To calculate the escape velocity of a celestial body, several factors come into play. These include the mass of the celestial body and the distance between the object and the center of the body. The formula for escape velocity is derived from the law of conservation of energy and Newton's law of universal gravitation.

The formula for escape velocity (Ve) is given as:

Ve = sqrt(2GM/R)

Where:

Ve is the escape velocity

G is the universal gravitational constant (approx. 6.67430 × 10^-11 m³kg^-1s^-2)

M is the mass of the celestial body (in this case, Earth)

R is the distance from the center of the celestial body to the object (in this case, the Earth's radius)

Escape Velocity of Earth

Applying the formula to Earth, we can determine its escape velocity. Earth's mass is approximately 5.972 × 10²⁴ kg, and its average radius is about 6,371 kilometers (6.371 × 10⁶ meters). Substituting these values into the formula, we can calculate Earth's escape velocity.

Ve = sqrt(2GM/R)

= sqrt(2 × (6.67430 × 10^-11) × (5.972 × 10²⁴) / (6.371 × 10⁶))

≈ 11,186 meters per second (m/s)

≈ 40,270 kilometers per hour (km/h)

≈ 25,020 miles per hour (mph)

Practical Implications and Applications

• Space Exploration: Escape velocity is a crucial factor in space exploration missions. It determines the minimum speed required for spacecraft to leave Earth's gravitational field and venture into space. Understanding Earth's escape velocity helps engineers design launch vehicles and plan trajectories for missions to other planets, moons, and celestial bodies.
• Satellite Launches: Satellites play a vital role in communication, weather monitoring, navigation, and scientific research. To place a satellite into orbit around Earth, it must reach a specific velocity known as orbital velocity. This velocity is lower than the escape velocity but still sufficient to counteract Earth's gravitational pull and maintain a stable orbit. Understanding escape velocity aids in calculating the necessary launch velocity to achieve the desired orbit for satellite deployment.
• Reentry and Atmospheric Escape: Escape velocity is also relevant for objects returning to Earth. When a spacecraft reenters Earth's atmosphere, it experiences significant deceleration due to atmospheric drag. The spacecraft must ensure that its reentry speed is high enough to overcome atmospheric drag but not so high that it burns up or experiences excessive heating. On the other hand, objects such as gases and particles in the Earth's atmosphere may escape into space if they attain a velocity higher than the escape velocity. Understanding Earth's escape velocity helps in studying the atmospheric escape phenomenon and its effects on the Earth's atmosphere.
• Geostationary Orbit: A geostationary orbit is an orbit in which a satellite appears to remain stationary above a particular point on Earth's surface. To maintain this position, the satellite must orbit at the same rate as Earth's rotation. Understanding Earth's escape velocity is crucial in determining the minimum height at which a satellite can orbit and still remain in a geostationary position.

Factors Influencing Earth's Escape Velocity

The escape velocity of a celestial body depends on its mass and radius. However, other factors also come into play and can influence the escape velocity of a planet. These include atmospheric drag, rotation, and gravitational interactions with other celestial bodies.

• Atmospheric Drag: The Earth's atmosphere exerts a drag force on objects that pass through it, such as spacecraft. This force reduces the object's velocity and can affect its trajectory. Therefore, objects launching from Earth's surface must attain a higher velocity than the escape velocity to compensate for the drag force and achieve escape velocity.
• Rotation: The Earth's rotation affects the escape velocity at different latitudes. The equator rotates faster than the poles, causing an outward centrifugal force that reduces the effective gravitational pull. Therefore, the escape velocity at the equator is slightly lower than at the poles.
• Gravitational Interactions: The gravitational pull of other celestial bodies, such as the Moon and the Sun, affects Earth's gravitational pull. The gravitational interactions between the Earth and these celestial bodies cause variations in the Earth's gravitational field, which can affect the escape velocity.

The Historical Significance of Escape Velocity

The concept of escape velocity has been instrumental in shaping our understanding of celestial mechanics and space exploration. It was first introduced by the brilliant physicist and mathematician Isaac Newton in his seminal work, "Philosophiæ Naturalis Principia Mathematica," published in 1687. Newton's laws of motion and universal gravitation laid the foundation for calculating escape velocity and revolutionized our understanding of how objects move in space.

The Space Age and Beyond

The knowledge of escape velocity became particularly crucial during the Space Age, which began with the launch of the Soviet satellite Sputnik 1 in 1957. Since then, numerous manned and unmanned missions have been launched into space, with escape velocity serving as a guiding principle in mission planning.

For example, the Apollo program, which successfully landed humans on the Moon, relied heavily on escape velocity calculations. The Apollo spacecraft needed to achieve the necessary escape velocity from Earth to break free from its gravitational pull and journey to the Moon. Precise calculations of escape velocity were critical in determining the required launch parameters and trajectory for the Apollo missions.

Furthermore, the exploration of other celestial bodies, such as Mars, Venus, and the outer planets, necessitated a thorough understanding of escape velocity. The escape velocities of these bodies differ from Earth's, and space probes and landers must attain the appropriate escape velocities to reach their destinations successfully.

Satellite Launches and Orbital Mechanics

Escape velocity also plays a pivotal role in satellite launches. Satellites are placed into various orbits around the Earth to serve different purposes, including communication, weather monitoring, and scientific research. To achieve a stable orbit, satellites must attain a specific velocity known as orbital velocity, which is typically lower than the escape velocity.

The orbital velocity is the minimum speed required for a satellite to counteract the gravitational force and maintain a circular or elliptical orbit around the Earth. By carefully calculating the escape velocity and the required orbital velocities, scientists and engineers can precisely plan satellite launches and determine the necessary fuel and energy requirements for achieving and maintaining the desired orbits.

Implications for Human Space Exploration

Escape velocity remains a significant consideration for future human space exploration endeavors. As we aspire to send astronauts on long-duration missions to other planets or even beyond our solar system, understanding escape velocity becomes vital for planning and executing these missions.

For instance, a mission to Mars would require astronauts to reach the escape velocity from Earth, travel to Mars, and then decelerate to enter the Martian orbit or make a controlled landing. Similarly, in future deep space missions, such as crewed voyages to distant asteroids or other star systems, escape velocity calculations will be critical for designing propulsion systems and determining the fuel and resources needed for these ambitious journeys.

New Horizons and Challenges

While our understanding of escape velocity has been instrumental in space exploration, there are still challenges and limitations to overcome. For instance, the concept assumes a spherically symmetric celestial body with a uniform gravitational field, which is an idealized representation. In reality, the shape, composition, and uneven distribution of mass within a celestial body can lead to variations in its gravitational field and, consequently, in its escape velocity.

Additionally, atmospheric drag, gravitational slingshots, and other dynamic factors in space add complexity to escape velocity calculations. These factors must be carefully considered to ensure accurate trajectory predictions and successful mission outcomes.

Conclusion

Escape velocity is a fundamental concept that plays a vital role in space exploration, satellite launches, and understanding the dynamics of celestial bodies. Earth's escape velocity, which is approximately 11,186 meters per second, is determined by its mass and radius. Several factors, such as atmospheric drag, rotation, and gravitational interactions, can also influence Earth's escape velocity. Understanding escape velocity is essential in designing launch vehicles, planning trajectories for missions, calculating orbital velocities, and studying atmospheric escape.

From the early days of the Space Age to current and future missions, escape velocity calculations are critical in planning satellite launches, exploring other celestial bodies, and envisioning human missions to distant destinations. As our knowledge and technology continue to advance, a deeper understanding of escape velocity will help us overcome challenges and pave the way for new frontiers in space exploration.