Bernoulli's Principle
Introduction
In the world of fluid dynamics, a simple yet profound principle governs the behavior of liquids and gases as they flow through various mediums. This principle, named after the Swiss mathematician and physicist Daniel Bernoulli, is aptly known as Bernoulli's Principle. This fundamental concept has far-reaching implications, from explaining the lift generated by aircraft wings to unraveling the mysteries of fluid behavior in various engineering and everyday scenarios.
What is Bernoulli's Principle?
Bernoulli's Principle, named after the Swiss mathematician and physicist Daniel Bernoulli, is a fundamental concept in fluid dynamics that describes the behavior of fluids (both liquids and gases) as they flow through a pipe or over a surface. Bernoulli's Principle states that as the speed of a fluid increases, its pressure within decreases, and vice versa. In other words, there is an inverse relationship between the speed and pressure of a fluid. This principle is derived from the conservation of energy along a streamline in a fluid flow.
Bernoulii's Principle can be understood from different points of view. Some ways to summarize the principle are:
- Faster Flow, Lower Pressure: When the velocity of a fluid increases (for example, when it flows through a narrow section of a pipe), the pressure of the fluid decreases. This phenomenon can be observed in the Venturi effect, where the constriction of a pipe causes an increase in fluid speed and a decrease in pressure.
- Slower Flow, Higher Pressure: Conversely, when the velocity of a fluid decreases (for instance, when it flows into a wider section of a pipe), the pressure of the fluid increases.
- Conservation of Energy: Bernoulli's Principle is a result of the conservation of energy in a fluid flow. As the fluid flows, its total energy, which includes kinetic energy (due to motion) and potential energy (due to elevation), remains constant along a streamline in the absence of external forces like friction or heat transfer.
The Mathematical Representation of Bernoulli's Principle:
Mathematically, Bernoulli's Principle can be expressed as follows:
P + ½ ρ*v 2 + ρ*g*h = constant
Where:
- P represents the pressure of the fluid.
- ρ denotes the density of the fluid.
- v symbolizes the velocity of the fluid.
- g stands for the acceleration due to gravity.
- h signifies the height above a reference point.
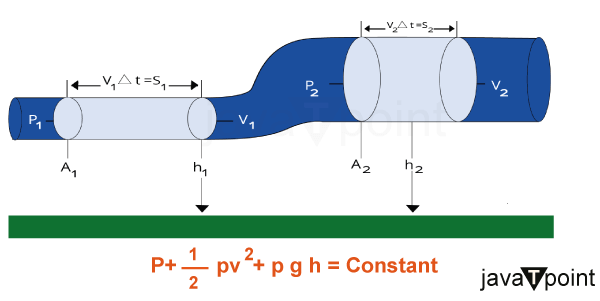
This equation illustrates energy conservation along a streamline in a fluid flow, where the total energy, comprising potential and kinetic energy, remains constant in the absence of external forces. As the fluid moves, its energy distribution changes due to variations in velocity and pressure.
Brief History of Bernoulli's Principle
The history of Bernoulli's Principle is intertwined with the contributions of several prominent mathematicians and physicists over the centuries. The development of the principle can be traced back to the 18th century, with Daniel Bernoulli being a central figure in its formulation. In the 17th century, mathematicians like Blaise Pascal and Evangelista Torricelli laid the groundwork for understanding fluid pressure. Torricelli's invention of the mercury barometer in 1643 demonstrated the concept of atmospheric pressure and fluid equilibrium.
Daniel Bernoulli made significant strides in formulating the fluid velocity and pressure relationship. He published his seminal work "Hydrodynamica" in 1738, which laid out the fundamental ideas of fluid dynamics and introduced what we now know as Bernoulli's Principle. In "Hydrodynamica," Bernoulli focused on energy conservation within fluid flow. He postulated that as a fluid speeds up, its kinetic energy increases at the expense of its potential energy, resulting in a decrease in pressure. This insight marked a crucial step toward understanding fluid behavior in various scenarios.

Applications of Bernoulli's Principle:
With its insights into fluid dynamics, Bernoulli's Principle finds a wide range of applications in various fields. This principle has been harnessed from engineering to everyday life to solve problems, design efficient systems, and enhance our understanding of fluid behavior. Here are some notable applications:
- Aviation:
One of the most famous applications of Bernoulli's Principle is in aviation. Aircraft wings are designed with a curved upper surface and a flatter lower surface. As air flows over the curved upper surface, it travels faster than the air beneath, reducing pressure on top and higher pressure on the bottom. This pressure difference creates lift, allowing airplanes to take flight and stay aloft.
- Wind Turbines:
The operation of wind turbines also relies on Bernoulli's Principle. The moving air over the curved blade surfaces results in a pressure difference, causing the blades to turn and generate mechanical energy that can be converted into electricity.
- Carburetors and Fuel Injection:
Bernoulli's Principle plays a vital role in the operation of engines. Carburetors and fuel injection systems utilize the principle to mix air and fuel in the right proportion for combustion. As air flows through a narrow passage, its speed increases, creating a low-pressure region. This low-pressure area draws fuel into the airstream, facilitating efficient combustion.
- Atomizers and Spray Nozzles:
Devices like perfume atomizers and spray nozzles exploit Bernoulli's Principle to create a fine liquid mist. As the liquid flows through a constriction, its speed increases, resulting in reduced pressure. This pressure drop causes the liquid to break into smaller droplets, creating a fine spray.
- Blood Circulation:
Bernoulli's Principle helps explain aspects of blood circulation within the human body. As blood flows through constricted vessels, its speed increases, causing a decrease in pressure. This principle is particularly relevant in understanding conditions like aneurysm and stenosis in blood vessels.
- Water Distribution Systems:
The principle is used in designing water distribution systems, such as water towers and pipelines. By understanding how pressure and velocity are related, engineers can optimize water flow in pipes to ensure efficient and reliable distribution.
- Airfoil Design and Sailboats:
Beyond aviation, Bernoulli's Principle is applied in designing airfoils (wing-like structures) for sailboats. The principle helps optimize the shape of sail surfaces to generate lift and propulsion as wind flows over them.
- Pitot Tubes and Speed Measurement:
Pitot tubes, commonly used in aircraft and weather stations, leverage Bernoulli's Principle to measure the speed of air or fluid flow. These tubes have openings that face the flow, and the pressure difference between the openings provides a measure of velocity.
- Ventilation and HVAC Systems:
The design of ventilation systems and heating, ventilation, and air conditioning (HVAC) systems involves understanding the principles of fluid dynamics. Bernoulli's Principle guides the efficient distribution of air within buildings to maintain comfortable environments.
- Sporting Equipment:
Various sports equipment, such as tennis balls and golf balls, are designed using Bernoulli's insights into fluid behavior. For example, the dimples on golf balls help reduce drag by manipulating airflow around the ball.
These applications highlight the versatility and significance of Bernoulli's Principle in diverse fields. While the principle may not provide a complete description of all fluid behaviors, its practical utility in designing systems, solving problems, and driving innovation are undeniable.
Some Daily Life Examples of Bernoulli's Principle:
The best way to grasp the concept of any principle or law is by observing its effect on daily life and the objects surrounding us. Some daily life examples of Bernoulli's Principle in effect are:
- Drinking with a Straw: When you sip a drink through a straw, you create a low-pressure area inside the straw by sucking on it. This decrease in pressure allows the higher atmospheric pressure to push the liquid up the straw and into your mouth, allowing you to enjoy your beverage.
- Blowing Up a Balloon: When you blow air into a balloon, you increase the air pressure. As the pressure inside the balloon becomes higher than the atmospheric pressure outside, the balloon inflates.
- Hair Dryers: Hair dryers use the principle to blow warm air. The fast-moving air generated by the hair dryer's motor creates a region of low pressure around the air outlet, drawing in cooler air from the surroundings. This mixed air is then blown out, allowing you to dry your hair quickly.
- Kite Flying: The lift generated by a kite in the sky results from Bernoulli's Principle. The wind passing over the surface of the kite's wings creates a pressure difference that lifts the kite into the air.
- Ceiling Fans: Ceiling fans help cool a room by circulating air. The curved shape of the fan blades causes air to move faster over the curved side, resulting in lower pressure. This creates a breeze that cools you as the air moves across your skin.
- Playing Musical Instruments: Many musical instruments, such as flutes and clarinets, rely on Bernoulli's Principle. As a player blows air across a narrow opening, the fast-moving air creates a region of low pressure, causing the column of air inside the instrument to vibrate and produce sound.
- Vacuum Cleaners: Vacuum cleaners use the principle to suck up dirt and debris from the floor. The motor creates a fast-moving stream of air that lowers the pressure inside the vacuum cleaner, allowing atmospheric pressure to push dirt and debris into the machine.
- Airplane Windows: The shape of airplane windows is designed to withstand the pressure difference between the cabin and the outside atmosphere. The curvature of the window helps distribute the pressure evenly, ensuring that the window doesn't break under the force of the pressure difference.
- Windshield Wipers on Cars: Windshield wipers use the principle to remove rainwater from the windshield effectively. As the wipers move across the glass, they create a region of low pressure that lifts and removes the water, allowing you to have clear visibility while driving in the rain.
- Spray Bottles: Spray bottles, used for cleaning, gardening, or personal care, work based on Bernoulli's Principle. As you squeeze the trigger, the liquid inside the bottle is forced through a narrow nozzle. The fast-moving liquid creates a low-pressure area, drawing in air and causing the liquid to spray out in a fine mist.
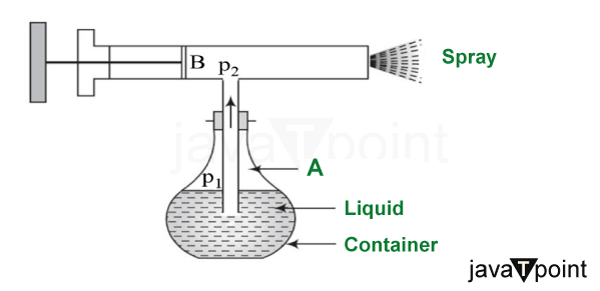
Venturi Effect a Consequence of Bernoulli's Principle:
The Venturi effect is a phenomenon in fluid dynamics. It states that in a situation with constant mechanical energy, the velocity of a fluid passing through a constricted area will increase and its static pressure will decrease. This effect is named after the Italian physicist Giovanni Battista Venturi, who first described it in the 18th century.
The Venturi effect is closely related to Bernoulli's Principle, as both concepts are based on energy conservation in fluid flow. The Venturi effect can be seen as a specific application or consequence of Bernoulli's Principle.
When a fluid flows through a constricted section of a pipe (the Venturi tube), its speed increases as it passes through the narrowest part. According to Bernoulli's Principle, as the fluid's speed increases, its pressure decreases. This pressure drop results from the fluid's kinetic energy increasing at the expense of its potential energy (pressure).
Explanation:
As fluid flows through the narrow section of the Venturi tube, it must accelerate to maintain the same flow rate. The principle of conservation of mass dictates that the mass flow rate (mass of fluid passing through a point per unit time) must remain constant. Since the flow area decreases in the narrow section, the fluid velocity increases to compensate for the reduced cross-sectional area.
According to Bernoulli's Principle, as the fluid's velocity increases, its pressure decreases. This is because the fluid's kinetic energy is increasing, and to maintain energy conservation, its potential energy (pressure) must decrease. Thus, the Venturi effect results in a lower pressure in the constricted section as compared to pressure in the same section before the constriction.
Practical Applications:
The Venturi effect has practical applications in various fields:
- It's used in carburetors to mix air and fuel efficiently in internal combustion engines.
- Venturi meters are used to measure fluid flow rates by measuring the pressure difference across a constriction.
- Atomizers and spray nozzles utilize the Venturi effect to create fine sprays.
- Siphoning liquids relies on the pressure difference created by the Venturi effect.
- Oxygen delivery in medical settings uses the Venturi effect to mix oxygen and air at specific ratios.
Drawbacks of Bernoulli's Principle:
While Bernoulli's Principle is a valuable concept that provides insights into fluid dynamics and has many applications, it also has limitations and drawbacks. Here are some of the drawbacks and considerations associated with Bernoulli's Principle:
- Viscosity and Friction:
Bernoulli's Principle assumes idealized fluid behavior with no internal friction or viscosity. In reality, fluids have viscosity, which can cause energy losses due to friction as they flow through surfaces or pipes. The principle might not accurately predict pressure distributions in situations involving viscous fluids, such as honey or oil.
- Incompressible Fluids:
Bernoulli's Principle most applies to incompressible fluids, such as liquids. For compressible fluids like gases, such as air, the density can change significantly with changes in pressure and temperature. In such cases, Bernoulli's Principle may not accurately represent fluid behavior.
- Turbulence:
In cases of turbulent flow, where chaotic and irregular fluctuations occur within the fluid, Bernoulli's Principle might not hold true. Turbulence involves complex interactions that can cause pressure variations that cannot be fully explained by the principle alone.
- Boundary Layer Effects:
The boundary layer is a thin layer of fluid that adheres to the surface of an object moving through it. Bernoulli's Principle doesn't account for the effects of boundary layers, which can influence the flow behavior near surfaces and lead to deviations from the idealized principle.
- Non-Streamline Flow:
Bernoulli's Principle is based on energy conservation along a streamline, representing a smooth path that fluid particles follow. In real-world scenarios, fluid flows can be non-uniform, with irregular eddies and mixing that deviate from streamline conditions.
- Simplified Assumptions:
The derivation of Bernoulli's Principle relies on certain simplifications, such as steady flow, inviscid (no viscosity) flow, and adiabatic (no heat exchange) flow. These assumptions might not hold true in all situations.
- Directional Changes:
When a fluid flow encounters changes in direction, such as sharp bends or turns, Bernoulli's Principle might not accurately predict pressure changes, especially if there are losses due to eddies and turbulence.
- Pressure Gradient:
Bernoulli's Principle focuses on the relationship between fluid velocity and pressure along a streamline. It doesn't provide a direct explanation for pressure changes caused by factors other than velocity changes, such as gravity-induced pressure gradients in vertical flows.
Modern Implications:
Modern interpretations of Bernoulli's Theorem have been shaped by advancements in fluid dynamics theories and computational methods, offering a deeper understanding of fluid behavior and allowing for more accurate predictions in complex scenarios. One of the key developments in this context is the Navier-Stokes equations.
- Navier-Stokes Equations:
The Navier-Stokes equations are a set of partial differential equations that describe fluid flow behavior, considering factors like viscosity, turbulence, compressibility, and external forces. These equations provide a more comprehensive and realistic framework for analyzing fluid dynamics compared to the simplified assumptions of Bernoulli's Principle.
- Advancements in Understanding:
The Navier-Stokes equations go beyond Bernoulli's Principle by incorporating concepts such as viscosity, which plays a critical role in real-world fluid flows. Viscosity causes internal friction within a fluid, leading to energy losses and complex flow patterns. The Navier-Stokes equations account for these effects, allowing engineers and scientists to model and predict fluid behavior in a wide range of situations.
- Turbulence Modeling:
One of the challenges that Bernoulli's Principle struggles to address is turbulent flow, which involves chaotic and irregular fluctuations within a fluid. Turbulence is common in many fluid systems, including air and water flow. Computational fluid dynamics (CFD) methods based on the Navier-Stokes equations have developed various turbulence models that help simulate and accurately predict turbulent flows.
- Computational Fluid Dynamics (CFD):
The advent of powerful computers and advanced numerical techniques has enabled the simulation of complex fluid dynamics scenarios using CFD. CFD involves numerically solving the Navier-Stokes equations to predict fluid behavior in intricate geometries, considering boundary conditions, turbulence, and multiphase flows. This approach allows engineers and researchers to gain insights into fluid dynamics that were previously inaccessible.
- Realistic Engineering Applications:
Modern fluid dynamics simulations based on the Navier-Stokes equations have led to significant advancements in engineering design. From aerodynamics in aerospace engineering to fluid flow in pipelines and environmental studies, these simulations provide a more accurate representation of fluid behavior, allowing for better optimization and design of systems.
Conclusion:
While Bernoulli's Principle remains a fundamental concept in fluid dynamics, the development of the Navier-Stokes equations and computational fluid dynamics methods has expanded our understanding of fluid behavior. These modern interpretations consider complexities such as viscosity, turbulence, and compressibility, providing a more comprehensive framework for analyzing fluid flow in diverse real-world scenarios. As technology continues to advance, our ability to predict and control fluid behavior will further improve, leading to innovative solutions in various fields.
|



 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









