Escape Velocity

Escape velocity is the minimum velocity required for an object to escape the gravitational pull of a celestial body, such as a planet or a moon. The concept of escape velocity is crucial to understanding the behavior of objects in space, including spacecraft and natural satellites. In this article, we will explore the concept of escape velocity, how it is calculated, and its applications in space exploration.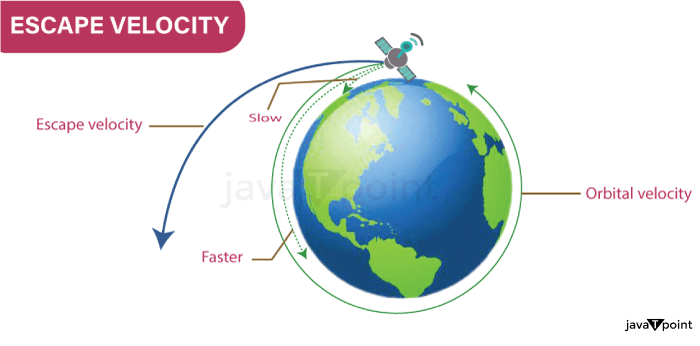

Gravity is a fundamental force that governs the motion of objects in the universe. It is the force that pulls objects towards each other and keeps them in orbit around each other. The strength of the gravitational force depends on the mass of the objects and the distance between them. The larger the mass of an object, the stronger its gravitational force. Similarly, the closer two objects are, the stronger their gravitational force.

Escape velocity is the velocity required for an object to escape the gravitational pull of a celestial body and move into space. If an object is launched with a velocity less than the escape velocity, it will eventually fall back to the surface of the celestial body. On the other hand, if the object is launched with a velocity greater than the escape velocity, it will escape the gravitational pull and move away from the celestial body.

The formula to calculate the escape velocity is given by:

v = sqrt(2GM/R)

where v is the escape velocity, G is the gravitational constant, M is the mass of the celestial body, and R is the distance from the center of the celestial body to the object's initial position.

The formula shows that the escape velocity is directly proportional to the mass of the celestial body and inversely proportional to the distance from the center of the celestial body. This means that the larger the mass of the celestial body or the closer an object is to its center, the greater the escape velocity required.

For example, the escape velocity of Earth is approximately 11.2 kilometers per second (km/s), while the escape velocity of the Moon is only 2.38 km/s. This means that it is easier to escape the Moon's gravitational pull than Earth's, as it requires less energy to reach the escape velocity.

Applications of Escape Velocity

• Escape velocity has several practical applications in space exploration. For example, spacecraft is launched with a velocity greater than the escape velocity to escape the Earth's gravitational pull and enter space. This requires a significant amount of energy and is achieved through the use of rockets.
• Once a spacecraft has escaped the Earth's gravitational pull, it can use the gravitational pull of other celestial bodies, such as planets, to change its trajectory and reach its destination. This technique is known as gravity assist and is commonly used in space missions.
• Escape velocity also plays a role in the behavior of natural satellites, such as the Moon. The Moon's gravitational pull affects the tides on Earth and is responsible for the phenomenon of tidal locking, where the same side of the Moon always faces the Earth. This occurs because the Moon's rotation is synchronized with its orbit around the Earth, and the gravitational pull of the Earth has slowed down the Moon's rotation over time.
• One interesting aspect of escape velocity is that it is a universal concept. It applies to any celestial body, regardless of its size or composition. For example, the escape velocity of the Sun is approximately 617.5 km/s, while the escape velocity of a black hole can be greater than the speed of light.
• Escape velocity also has implications for the colonization of other planets and moons in our solar system. For example, Mars has a lower escape velocity than Earth, which means that it is easier to launch spacecraft from its surface. However, Mars also has a weaker gravitational pull, which can have long-term effects on the health of human colonizers. On the other hand, the moons of Jupiter and Saturn have higher escape velocities than Earth, which makes it more difficult to launch spacecraft from their surfaces. However, their strong gravitational pull can provide a protective shield from cosmic radiation, which is a significant risk for long-term human space exploration.
• Another important aspect of escape velocity is that it is not a fixed value. It depends on the distance from the center of the celestial body, which means that the escape velocity changes as the object moves further away from or closer to the body. This is an important consideration for spacecraft that are sent on long-duration missions, as their trajectory and velocity can be affected by the gravitational pull of other celestial bodies.
• Escape velocity is also related to the concept of geostationary orbit. A geostationary orbit is an orbit around the Earth where a satellite appears to be stationary relative to a fixed point on the Earth's surface. This is achieved by placing the satellite in an orbit that has the same period as the Earth's rotation, which is approximately 24 hours. To maintain a geostationary orbit, a satellite must have a specific velocity, which is known as the geostationary velocity. This velocity is calculated using the same formula as the escape velocity, but with the distance from the center of the Earth replaced by the distance from the center of the geostationary orbit.
• Escape velocity is also important for understanding the behavior of comets and asteroids. These objects are often in highly elliptical orbits around the Sun, which means that they experience significant changes in their velocity as they move closer to or further away from the Sun. If an object's velocity exceeds the escape velocity of the Sun, it can be ejected from the solar system and become a rogue planet or interstellar object.

Conclusion

It is related to many other concepts, such as gravity, geostationary orbit, and the behavior of comets and asteroids. As we continue to explore the solar system and beyond, the escape velocity will remain an important consideration for space missions and the colonization of other planets and moons.

In conclusion, escape velocity is a fundamental concept in space exploration and the behavior of objects in space. It is the minimum velocity required for an object to escape the gravitational pull of a celestial body and move into space. The formula for escape velocity shows that it is directly proportional to the mass of the celestial body and inversely proportional to the distance from its center. This means that the larger the mass of the celestial body or the closer an object is to its center, the greater the escape velocity required. The practical applications of escape velocity include launching spacecraft into space, using gravity assist to change trajectory, and understanding the behavior of natural satellites.