Escape Velocity Formula

Escape velocity is the minimum speed an object needs to achieve in order to break free from the gravitational pull of another object. This concept is fundamental in space exploration and in understanding how planets, moons, and other celestial bodies behave. The escape velocity formula is a mathematical expression that calculates the speed an object must attain to escape the gravitational pull of another object.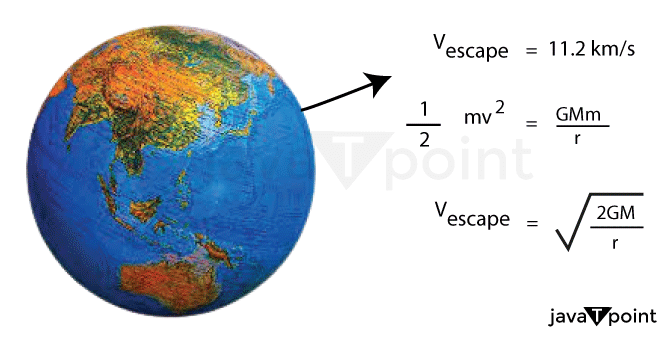

The escape velocity formula is given by:

v = √(2GM/r)

Where:

• v is the escape velocity of the object,
• G is the gravitational constant (6.674 × 10^-11 N m²/kg²),
• M is the mass of the object from which the object is escaping,
• r is the distance between the centers of the two objects.

Derivation

The formula is derived from the conservation of energy principle. When an object is at a distance r from a planet or other massive object of mass M, it has potential energy due to the gravitational force between the two objects. If the object were to move away from the planet, the gravitational force would do work on it, converting its potential energy into kinetic energy. To escape the planet's gravitational pull, the object must have enough kinetic energy to overcome its potential energy.

The escape velocity formula can be derived using the conservation of energy principle. The potential energy of an object at a distance r from a planet of mass M is given by:

U = -GMm/r

Where m is the mass of the object.

The kinetic energy of the object can be expressed as:

K = (1/2)mv²

Where v is the velocity of the object.

The total energy of the object is the sum of its kinetic and potential energy:

E = K + U

If the object is at rest at a distance r from the planet, then its kinetic energy is zero, and its total energy is equal to its potential energy:

E = U = -GMm/r

As the object moves away from the planet, its potential energy decreases while its kinetic energy increases. At the point where the object just escapes the planet's gravitational pull, its total energy is zero, which means that its kinetic energy is equal to the magnitude of its potential energy:

K = -U

Substituting the expressions for K and U, we get:

(1/2)mv² = GMm/r

Solving for v, we get:

v = √(2GM/r)

This is the escape velocity formula.

Applications of Escape Velocity

• The escape velocity formula is important in many fields, including astronomy, astrophysics, and space travel. For example, the formula is used to calculate the escape velocity of rockets leaving Earth's atmosphere. The escape velocity of Earth is approximately 11.2 km/s, which means that a rocket must achieve this speed in order to escape Earth's gravitational pull. If the rocket's speed is less than the escape velocity, it will not be able to escape Earth's gravity and will either fall back to Earth or remain in orbit.
• The escape velocity formula is also used to calculate the escape velocities of other celestial bodies, such as moons and planets. For example, the escape velocity of the Moon is approximately 2.4 km/s, while the escape velocity of Jupiter is approximately 59.5 km/s. These values have important implications for space exploration and the study of celestial bodies.
• One important application of the escape velocity formula is in space exploration. For example, when launching a spacecraft from Earth, the escape velocity must be reached in order to break free from the Earth's gravitational pull and enter space. The escape velocity from the Earth's surface is approximately 11.2 kilometers per second (km/s), which is much greater than the speed of sound (340 meters per second) and the speed of most aircraft.
• The escape velocity formula can also be used to determine the maximum speed at which an object can approach a planet or other massive object without being captured by its gravitational pull. This speed is known as the "capture velocity" or "parking velocity". The capture velocity is equal to the escape velocity multiplied by the square root of 2. If an object is traveling slower than the capture velocity, it will be captured by the planet's gravity and will enter into an orbit around it.
• The escape velocity formula is also important in the study of black holes. A black hole is an object with an extremely strong gravitational pull, so strong that not even light can escape from it. The escape velocity from a black hole is greater than the speed of light, which means that nothing can escape from it once it crosses the event horizon, the point of no return. The escape velocity formula can be used to calculate the event horizon of a black hole, which is the distance from the center of the black hole at which the escape velocity is equal to the speed of light.

In addition to the escape velocity formula, there are other factors that can affect an object's ability to escape the gravitational pull of another object. For example, the shape and rotation of the object can affect its escape velocity. If an object is elongated, it will have a lower escape velocity than a spherical object of the same mass and size. Similarly, if an object is rotating, its escape velocity will be lower at the equator than at the poles.

The escape velocity formula is also related to the concept of gravitational potential energy. The gravitational potential energy is the amount of work required to move an object from one point to another against the gravitational force. The gravitational potential energy of an object of mass m at a distance r from a planet or other massive object of mass M is given by:

U = -GMm/r

This equation shows that the gravitational potential energy is negative, which means that the potential energy decreases as the object moves further away from the planet. The potential energy at infinity is zero, which means that an object that is infinitely far away from the planet has zero potential energy.

The escape velocity formula can be derived using the concept of gravitational potential energy. If an object is to escape from the gravitational pull of a planet, it must have enough kinetic energy to overcome its potential energy.

The escape velocity formula is also related to the concept of gravitational acceleration. The gravitational acceleration is the acceleration experienced by an object due to the gravitational force. The gravitational acceleration at a distance r from a planet or other massive object of mass M is given by:

g = GM/r²

This equation shows that the gravitational acceleration decreases as the object moves further away from the planet. The gravitational acceleration at infinity is zero, which means that an object that is infinitely far away from the planet has zero gravitational acceleration.

The escape velocity formula can be related to the gravitational acceleration by using the equation for kinetic energy:

K = (1/2)mv²

If an object is to escape from the gravitational pull of a planet, it must have enough kinetic energy to overcome its potential energy. The minimum kinetic energy required to escape is equal to the magnitude of the potential energy:

K = -U

Substituting the expressions for K and U, we get:

(1/2)mv² = GMm/r

Solving for g, we get:

g = v²/r = GM/r²

This equation shows that the gravitational acceleration at a distance r from a planet is equal to the square of the escape velocity divided by the distance from the planet.

The escape velocity also varies with the mass and radius of the planet or object from which an object is escaping. For example, the escape velocity from the surface of the Moon is much lower than the escape velocity from the surface of Earth. This means that it takes less energy to launch a spacecraft from the Moon than from Earth. The escape velocity from the surface of the Moon is approximately 2.4 km/s, which is less than one-fourth of the escape velocity from the Earth.

In addition to the escape velocity formula, there are other equations and concepts related to escape velocity. For example, the Tsiolkovsky rocket equation relates the change in velocity of a spacecraft to the mass of its propellant and the exhaust velocity of the rocket. This equation is important in the design of spacecraft and rocket engines. The concept of gravitational slingshot, or gravitational assist, is another important concept related to escape velocity. This technique involves using the gravitational pull of a planet or other celestial body to increase the speed of a spacecraft without using additional fuel.

Conclusion

In summary, the escape velocity formula is a fundamental equation in physics that is used to calculate the speed an object must attain to escape the gravitational pull of another object. It is important in many fields, including astronomy, astrophysics, and space travel. The formula can be derived from the conservation of energy principle and is related to the concepts of gravitational potential energy and gravitational acceleration. The escape velocity formula has important applications in space exploration, the study of black holes, and the design of spacecraft and rocket engines.

It is derived from the conservation of energy principle and is important in many fields, including astronomy, astrophysics, and space travel. The escape velocity formula is related to the concepts of gravitational potential energy and gravitational acceleration and has important implications for the study of celestial bodies.