Terminal Velocity

Terminal velocity refers to the maximum velocity an object can achieve while falling through a fluid, such as air or water. It occurs when the force of gravity pulling the object downward is balanced by the drag force exerted by the fluid. At this point, the object stops accelerating and continues to fall at a constant speed.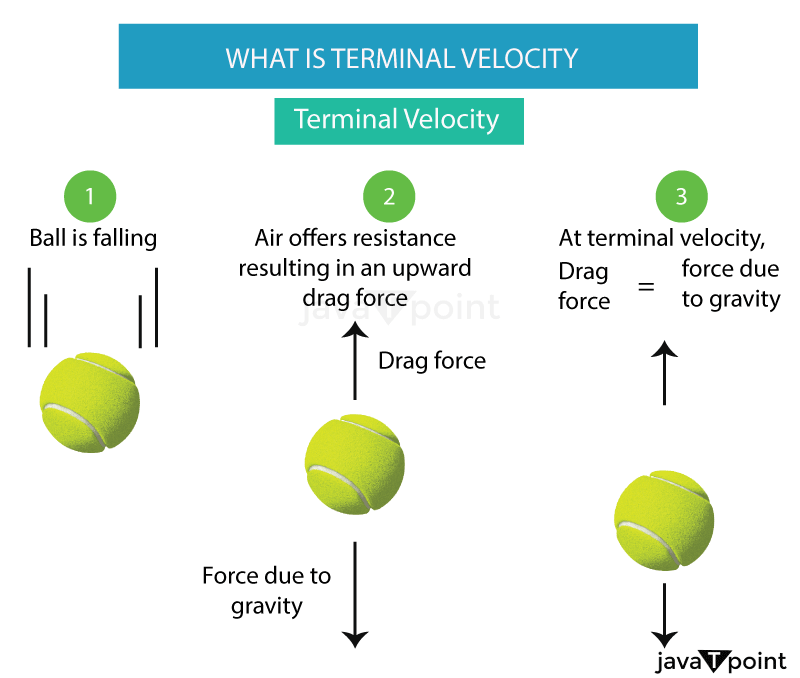

Where do We Use Terminal Velocity?

The concept of terminal velocity is important in various fields, including physics, engineering, and skydiving. Understanding terminal velocity helps scientists and engineers analyze the behavior of objects in fluid environments and design systems that can withstand the forces involved. In this article, we will explore the factors affecting terminal velocity, the equations used to calculate it, and some practical applications.

• Practical applications of terminal velocity can be found in various fields. For example, in skydiving, understanding terminal velocity helps divers determine the appropriate time to deploy their parachutes. Skydivers initially accelerate due to gravity until they reach a point where the drag force from the air resistance equals their weight. This is when they achieve terminal velocity. By knowing their body position and the effects of air density and pressure, skydivers can estimate their terminal velocity and make informed decisions about when to open their parachutes for a safe descent.
• Terminal velocity is also important in engineering and design. Engineers must consider the effects of fluid dynamics on objects moving through air or water. For instance, when designing buildings or structures in areas prone to high winds, understanding the terminal velocity of debris or projectiles can help ensure that the structure can withstand potential impacts. By calculating the terminal velocity, engineers can determine the potential forces involved and design structures accordingly.
• In the field of aerodynamics, understanding terminal velocity is crucial for designing aircraft. Engineers analyze the drag forces acting on an aircraft at various speeds to optimize its performance. By considering factors such as the shape of the aircraft, its surface area, and the density of the air, engineers can determine the maximum speed an aircraft can reach and design it accordingly. Additionally, terminal velocity is essential in calculating the descent rate of aircraft during landing approaches, ensuring a safe and controlled landing.
• Furthermore, terminal velocity is relevant in the study of meteorology and atmospheric science. It helps explain the behavior of falling precipitation, such as raindrops or snowflakes. Understanding terminal velocity aids meteorologists in predicting how quickly precipitation will reach the ground and in estimating precipitation rates during weather events. It also plays a role in cloud formation, as the terminal velocity of water droplets or ice crystals influences their motion within the atmosphere.

To understand terminal velocity, we first need to comprehend the forces acting on a falling object. When an object is in free fall, it experiences two primary forces: gravity and drag. Gravity pulls the object downward, while drag opposes its motion through the fluid. The drag force depends on the shape, size, and speed of the object, as well as the properties of the fluid. When an object first starts falling, it accelerates due to the force of gravity. However, as the object accelerates, the drag force increases until it becomes equal to the force of gravity. At this point, the net force on the object is zero, and it reaches its maximum velocity, known as terminal velocity.

Factors Influencing Terminal Velocity

• Several factors influence terminal velocity. The most significant factor is the object's mass or weight. Heavier objects experience a stronger gravitational force and, therefore, reach higher terminal velocities. Another critical factor is the shape and size of the object. Objects with a larger surface area experience more drag, which reduces their terminal velocity
• The properties of the fluid through which the object is falling also play a crucial role in determining terminal velocity. For example, in gases like air, the density and viscosity affect the drag force. Higher density and viscosity result in higher drag forces, reducing the terminal velocity. Similarly, in liquids like water, the density and viscosity of the fluid impact the terminal velocity of objects falling through it.
• Moreover, terminal velocity can differ depending on the altitude or depth at which the object is falling. For example, at higher altitudes, where the air density is lower, objects experience lower drag forces, leading to higher terminal velocities. Similarly, in water, where the density is higher than air, terminal velocities for objects falling through it will be different than those in air.
• Terminal velocity can also be influenced by the presence of additional forces acting on the object. For instance, if an object is equipped with wings or control surfaces that generate lift or maneuvering forces, it can affect the terminal velocity by altering the balance between gravitational and drag forces. This is particularly relevant in sports like skydiving or wingsuit flying, where participants manipulate their body positions or use specialized suits to modify their terminal velocities.

Calculation of Terminal Velocity

To calculate the terminal velocity of an object, several equations are used, depending on the specific conditions and assumptions. One commonly used equation is derived from the drag equation. The drag force (F_d) is given by the equation:

F_d = 0.5 * ρ * A * C_d * v²

Where, ρ represents the density of the fluid,

A is the cross-sectional area of the object perpendicular to the direction of motion,

C_d is the drag coefficient that depends on the object's shape, and

v is the velocity of the object.

The drag force is proportional to the square of the velocity, indicating that as the velocity increases, the drag force also increases. At terminal velocity, the drag force equals the force of gravity (F_g = m * g), where m is the mass of the object, and g is the acceleration due to gravity. Setting F_d equal to F_g gives:

0.5 * ρ * A * C_d * v² = m * g

Rearranging the equation and solving for v, we obtain the expression for terminal velocity (v_t):

v_t = sqrt ((2 * m * g) / (ρ * A * C_d))

This equation shows that the terminal velocity is proportional to the square root of the mass and the ratio of the acceleration due to gravity and the fluid properties. It is important to note that this equation assumes the object reaches a steady state without any further acceleration or changes in the fluid properties.

Terminal velocity is not limited to just falling objects. It can also be observed in the upward motion of objects propelled through a fluid, such as rockets or airplanes. In these cases, the force of propulsion counteracts the force of drag until the object reaches a point where the two forces balance out, resulting in a constant upward velocity known as terminal velocity.

It is worth noting that the concept of terminal velocity assumes ideal conditions, such as a uniform fluid medium and no external factors affecting the object's motion. In reality, factors like wind gusts, turbulence, or changes in fluid density can affect the actual terminal velocity experienced by an object.

Another interesting phenomenon related to terminal velocity is the concept of a "terminal velocity barrier." This occurs when an object initially falls through a fluid and reaches a certain velocity, but cannot surpass it due to a shift in its orientation or shape. This barrier is caused by a sudden increase in drag, preventing the object from achieving higher speeds and altering its trajectory. Understanding this phenomenon is important in designing high-speed vehicles or projectiles to avoid sudden decreases in performance or stability.

Conclusion

In conclusion, terminal velocity is a fundamental concept in fluid dynamics and plays a crucial role in various fields. It helps scientists, engineers, and practitioners understand and predict the behavior of objects moving through fluids. By analyzing factors such as mass, shape, size, fluid properties, and external forces, one can calculate terminal velocity and make informed decisions in fields such as engineering, aviation, meteorology, and sports. As our understanding of fluid dynamics continues to evolve, the concept of terminal velocity will remain an essential tool in the design and analysis of objects in fluid environments.

Terminal velocity is the maximum speed an object can attain while falling through a fluid. It occurs when the force of gravity pulling the object downward is balanced by the drag force exerted by the fluid. Terminal velocity depends on factors such as the object's mass, shape, size, and the properties of the fluid. Equations derived from the drag force equation can be used to calculate terminal velocity. Understanding terminal velocity is crucial in fields such as physics, engineering, skydiving, aerodynamics, and meteorology. It allows scientists, engineers, and practitioners to analyze and predict the behavior of objects in fluid environments, design structures to withstand forces, optimize performance, and make informed decisions for various applications