Average Velocity

The average pace at which an object changes its position over a predetermined amount of time is referred to as average velocity in physics. This is a fundamental idea in physics that is applied in a variety of fields, including kinematics, dynamics, and thermodynamics. We will examine average velocity in this post, including what it is, how to calculate it, and when to use it.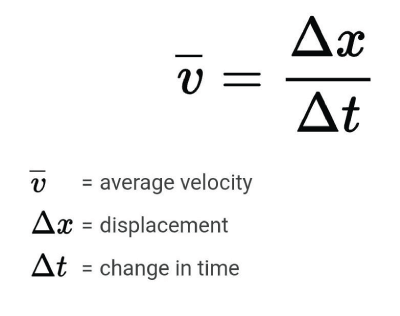

What is Average Velocity?

We must first comprehend the idea of velocity before we can comprehend average velocity. A vector number called velocity is used to explain how quickly an object changes its position with respect to time. The equation v = x/t, where v is the velocity, x is the change in the object's position, and t is the change in time, is used to describe it. Velocity can be defined as an object's speed and direction in the simplest terms. A car would have a velocity of 50 mph north, for instance, if it were traveling at 50 mph north.

The average pace at which an object changes its position over a predetermined amount of time is known as average velocity, on the other hand. By dividing the total change in time by the total change in location, it is determined. The formula:

v_avg = x_total/t_total,

where v_avg is the average velocity, x_total is the total change in the object's position, and t total is the total change in time, is used to describe it.

Instantaneous velocity, which is the speed of an item at a certain moment in time, is distinct from the average velocity. By considering the derivative of the position function with respect to time, one can determine the instantaneous velocity.

How is Average Velocity Calculated?

We need to know an object's initial location, final position, and the amount of time it takes to move from the initial position to the final position in order to determine its average velocity. To further comprehend this, let's look at an illustration.

Let's say an automobile drives 100 miles in two hours. Point A is where it starts, and point B is where it ends up. We must apply the calculation to determine the car's average speed:

V _avg = X_TOTAL / T_TOTAL

X total = x B - x A => 100 miles - 0 miles = 100 miles;

t total = t B - t A => 2 - 0 = 2 hours

As a result, the car's average speed is given by the formula: v avg = 100 / 2 = 50 mph.

This means that the car travelled at an average velocity of 50 mph from point A to point B.

How is Average Velocity Applied in Physics?

Average velocity is a fundamental idea in physics that is applied in a variety of contexts. Let's look at some of the applications for it:

• Kinematics: The area of physics known as kinematics examines how objects move without taking into account the forces that propel them. In kinematics, average velocity is a crucial term since it enables us to comprehend an object's total motion. We can figure out how far and how quickly an object has moved over a specific amount of time by computing its average velocity.
• Dynamics: The area of physics that deals with the forces that propel motion is called dynamics. The work a force does on an item is calculated in dynamics using average velocity. Work is referred to as the result of force and displacement, where displacement refers to a change in the object's location. We may determine an object's displacement and, consequently, the amount of work done on it by computing its average velocity.
• Thermodynamics: The study of heat and temperature is covered under the field of physics known as thermodynamics. The average speed of molecules in a gas can also be determined using average velocity in thermodynamics. The relationship between a gas's average molecular speed and temperature is straightforward. The temperature of the gas can be calculated by computing the average velocities of the molecules.

Average velocity is also used in many practical applications, such as calculating the speed of a moving vehicle, the velocity of a rocket, or the speed of an aircraft. It is also employed in sports to evaluate athletes' performance. For instance, a sprinter's average velocity can be used to calculate how quickly it covered a specific distance.

Other types of velocity, such as starting velocity, ultimate velocity, and instantaneous velocity, are employed in physics in addition to average velocity. Instantaneous velocity is the speed of an object at a single moment in time, while initial velocity and final velocity are the speeds of an object at the beginning and end of its motion, respectively.

Displacement is a key idea in the average velocity context. The movement of an object from its original position to its end position is referred to as displacement. It is a vector quantity, and its representation is given by the equation x = x_f - x_i, where x is the displacement and x_f, x_i, and x_f, respectively, are the final position and beginning position. Displacement is a crucial idea in physics because it enables us to comprehend an object's total motion.

Another method for determining an object's motion direction is to utilise average velocity. The direction of motion of an object moving in a straight line can be established by the sign of displacement. The object is travelling in the positive direction if the displacement is positive, and in the negative direction if the displacement is negative. The direction of motion is not always the same as the direction of the displacement, though, if the object moves along a curved path.

It is significant to remember that average and instantaneous velocities are not always the same. An object's instantaneous velocity is its speed at that precise moment in time, but its average velocity is the average rate at which its position changes over time. The instantaneous velocity and average velocity of an object may differ if its velocity is not constant.

Finally, it's critical to comprehend the restrictions placed on the use of average velocity. Average velocity merely conveys data about an object's general motion; it does not provide data about the precise mechanics of the motion. For instance, it doesn't provide information on the object's acceleration or how its velocity varies over time. We must make use of additional ideas, such as acceleration and instantaneous velocity, in order to gather this data.

Conclusion

In conclusion, average velocity is a crucial idea in physics that aids in our comprehension of how objects move over time. By dividing the total change in time by the total change in location, it is determined. Average velocity is a fundamental concept in many branches of physics and is also used in real-world contexts to evaluate the efficiency of machines and athletes. We can better understand an object's overall motion by connecting the notions of displacement and direction of motion.

Even though average velocity has its limitations, it is nonetheless a fundamental idea in physics and a vital tool for understanding how objects move. We may better grasp the motion of objects and how they respond in various scenarios by knowing the idea of average velocity.