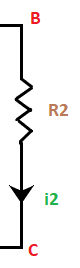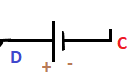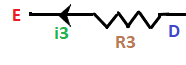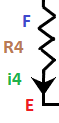Kirchhoff's law

Kirchhoff law was named after the German physicist named Gustav Robert Kirchhoff. He also contributed to the understanding of black body radiation and spectroscopy.

He first discovered the law in 1845. It forms the basis of network analysis and is generally applied in circuits' time and frequency domain. It is also known as Kirchhoff's circuit law.

Kirchhoff's law is also applied in the heat transfer, which is called Kirchhoff's law of radiation. Here, we will discuss both the Kirchhoff's circuit law in network analysis and Kirchhoff's law of radiation.

1. Kirchhoff's circuit law

There are two Kirchhoff's laws, which are as follows:

• The Junction Law
• The Loop Law

Let's discuss both the laws in detail.

The Junction Law

It is also known as the first Kirchhoff law. According to the Junction law,

"The sum of all the currents in a circuit directed inward or outward towards a point is equal to the sum of current directed outward or inward towards the same point."

The above junction law states that the sum of current elements directed inward is equal to the sum of current elements directed outwards towards the same point. Let's consider an example shown below: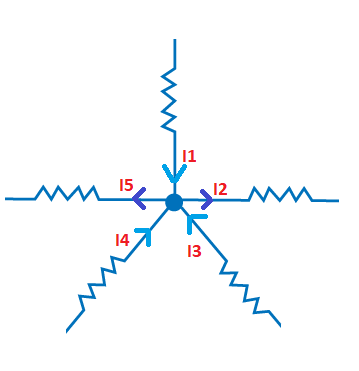

We can write the current elements as:

I1 + I3 + I4 = I2 + I5

The left side represents the current elements directed inwards, and the right side represents the current elements directed outwards.

The inward-directed current element is generally considered as positive in circuits, while the outward-directed current element is considered as negative. On this basis, the junction law can also be described as: "The algebraic sum of all the current elements directed towards a point is zero."

According to the above diagram, the current I1, I3, and I4 are directed inwards, while the current I2 and I5 are directed outwards. Considering the inward direction as positive and outwards direction as negative, we can write the equation as:

I1 + (-I2) + I3 + I4 + (-I5) = 0

By further solving, we get:

I1 + I3 + I4 = I2 + I5

It is same as the equation number 1.

The Kirchhoff's Junction law explains that no point in a circuit keeps on supplying the charge. The charge passes through such points in a circuit. The charge leaving the point is equal to the net charges coming towards it at the same time.

The Loop Law

In the junction law, we have discussed the current elements, and here, we will discuss the potential differences or the voltage elements.

We know,

I = V/R

Or

V = IR

So, the potential differences (V1 - V2) will be represented in the form of IR.

According to the loop law,

"The algebraic sum of all the potential differences along a closed loop in a circuit is zero."

The loop is in the shape of a circle. The direction of a loop can be clockwise or anticlockwise. The potential drop is considered as positive and the potential rise in the loop is considered as negative. The net sum of all the potential drops across all the points should be equal to zero. The loop starts from a point, and after passing through all the points, it reaches the same point.

Let's consider an example.

Example: The circuit is shown below: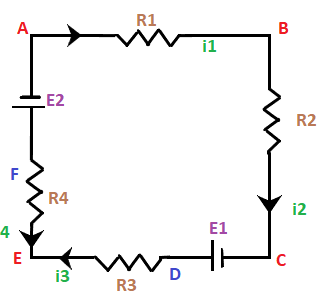

The loop of the above circuit is ABCDEFA. It is because the circuit has four points, A, B, C, E at the corners and two points D and F neat the potential drops. We will first write the equations for all the potential differences and will add those at the end.

Here, we have assumed the direction of the loop as clockwise, as shown below: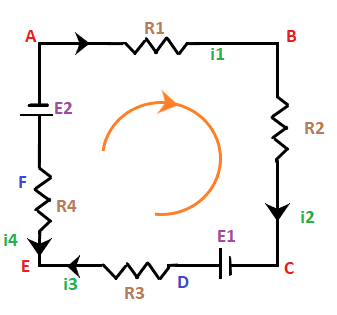

The sum of the potential differences will be equal to zero. The potential differences of the circuit are as follows:

1. For the branch between points A and B
   VA - VB = i1R1
   
   The direction of the current was the same as that of the loop. Hence, we will insert a positive sign with the current.
2. For the branch between points B and C
   VB - VC = i2R2
   
   Here also, the direction of current is the same as that of the loop.
3. For the branch between points C and D
   There is a voltage rise in the points between C and D.
   VC - VD = -E1
   
   As per the direction of the loop, the negative terminal of the battery comes first. Hence, the negative sign will appear with the potential E1.
4. For the branch between points D and E
   VD - VE = i3R3
   
5. For the branch between points E and F
   VE - VF = -i4R4
   
   We have inserted the negative sign with the current because the direction of the current i4 is in the opposite direction as that of the loop.
6. For the branch between points F and A
   VF - VA = E2
   
   As per the direction of the loop, the positive terminal of the emf or battery comes first. Hence, the positive sign will appear with the potential E1.

When we will add all the potential differences on the left-hand side, we will get the sum as zero. The equation after adding all the potential drops, we get:

0 = i1R1 + i2R2 -E1 + i3R3 -i4R4 + E2

Kirchhoff's loop law is based on the concept that the electrostatic force is a conservative force, which means that the work done is independent of the path. Hence, the work done by such force in any closed path is zero.

Applications of Kirchhoff's circuit law

The applications of Kirchhoff's law are as follows:

• It is used in the analysis of complex circuits.
• It helps us to predict the working of current and voltage in a circuit.

Drawbacks of Kirchhoff's circuit law

Kirchhoff's law also includes drawbacks like other laws in physics. Kirchhoff's law works on the basis that there is no magnetic field fluctuation in the circuit on which it is applied. It is known as the assumption of Kirchhoff's law. Kirchhoff has considered it as an assumption because a varying magnetic field can break the law.

2. Kirchhoff's law of radiation

Kirchhoff's law of radiation describes that the good absorbers of radiations (atoms taking up the photon's energy) are also good radiators (having high thermal conductivity).

According to Kirchhoff's law of radiation,

"The ratio of the emissive power to absorptive power (ratio = emissive power/absorptive power) is the same for all the bodies at a given temperature. It is equal to the emissive power of a blackbody (a body that absorbs all radiations) at that temperature."

It is given by:

E of a blackbody = Emissive power/ Absorptive power

E = E/A

Let's first discuss the terms emissive power and absorptive power.

Emissive power

Emission means the radiations emitted by the body. The energy emitted from a body would be emitted at a certain angle and at a specific time. It would also specify the area of emission, which means that radiations spread in a given area, as shown below: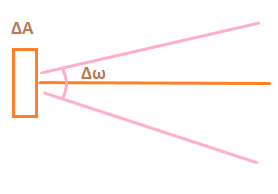

Thus, the emission power is expressed as the energy radiated per unit area, per unit time, and per unit solid angle.

It is given by: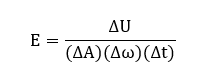

Where,

A is the area, w is the solid angle, and t is the time

The delta preceding the three terms (solid angle, time, and area) represents the dimensions in the small quantity. The numerator and denominator of the fraction in the emissive power formula are not similar. Hence, the emissive power is not a dimensionless unit, while the absorptive power is a dimensionless unit.

Absorptive power

Absorption means incident radiations that the body can easily absorb. Thus, absorptive power is defined as the power of the body expressed as the fraction of the incident radiations that are absorbed by the body. It is given by:

A = energy absorbed/ energy incident

Absorptive power is fraction of the energy with the energy only. Both the terms in the fraction have the same unit. Thus, we can say that absorptive power is a dimensionless unit.

In case of the blackbody, all the incident radiation on the body is absorbed. Hence, the absorptive power of the blackbody is unity.

Example of Kirchhoff's law

We know that Kirchhoff's law is given by:

E of a blackbody = Emissive power/ Absorptive power

E = E/A

According to Kirchhoff's law, a body with high emissive power would also have high absorptive power. Similarly, a body with low emissive power would also have low absorptive power.

Let's consider a practical example that will prove Kirchhoff's law of radiations.

The below figure shows two bodies, P and Q, placed in an enclosure with a constant temperature. Both the bodies will be at the same temperature. Body Q is a blackbody, while body P is a random body with the same geometrical shapes, as shown below: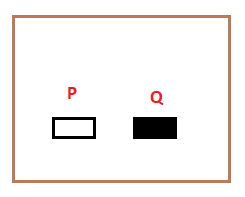

Suppose an amount of U radiations falls on the two bodies. Body Q, being the blackbody will absorb all of the incident radiations at a time t. The body Q will also emit the same radiations at a same temperature. If the emissive power of the body Q is Eo, the incident radiations is given by:

U = kEo ... (1)

Where, k is the constant.

But, body P will not absorb all of the incident radiations because it is not a blackbody. Thus, it absorbs the amount of radiation aU. Here, 'a' is the absorptive power of body P. The radiations emitted by the body will be aU, because the temperature of the enclosure is the same at that time. If the emissive power of the body P is E, the incident radiations is given by:

aU = kE ... (2)

Where, k is the constant.

We have specified the constant 'k' in both the derivations because the bodies are identical and emit radiations at the same time and temperature.

Equating both the equations 1 and 2, we get:

kEo = kE/a

a = E/Eo

Or

E/a = Eo

E/a = Eo (blackbody)

The above equation is the same as described in Kirchhoff's law of radiations (E of a blackbody = Emissive power/ Absorptive power). Hence, Kirchhoff's law is proved.