Adjacency List in C++

In this article, you will learn about the adjacency list in C++ with its different methods and implimentations.

Graph Representation:

A graph is a collection of nodes (vertices) and edges that connect these nodes. Graphs can be categorized into various types, including directed and undirected graphs, weighted and unweighted graphs, cyclic and acyclic graphs, etc. To perform operations or algorithms on graphs, they need to be represented in a way that computers can efficiently manipulate.

Adjacency List:

An adjacency list is a popular way to represent a graph, especially when the graph is sparse (contains fewer edges than the maximum possible edges). In an adjacency list, each vertex in the graph is associated with a list of its neighboring vertices. This representation efficiently captures the connectivity of the graph.

An adjacency list is a data structure representing connections between vertices in a graph. It is particularly useful for sparse graphs, where the number of edges is significantly smaller than the total possible number of edges. In an adjacency list, each vertex in the graph is associated with a list of its neighboring vertices.

In C++, you can implement an adjacency list using various data structures, such as an array of linked lists, a vector of vectors, or a map from vertices to their neighbors.

Directed Graphs:

A directed graph, also known as a digraph, is a type of the graph in which edges have a specific direction, indicating an one-way relationship between vertices. Unlike undirected graphs, where edges represent a connection between vertices without direction, directed graphs capture asymmetric relationships or dependencies between elements.

In a directed graph, each edge has an initial vertex (tail) and a terminal vertex (head), denoted by an arrow pointing from the tail to the head. This arrow indicates the direction of the relationship or flow represented by the edge. This concept of direction gives directed graphs a different set of characteristics and behaviors than undirected graphs.

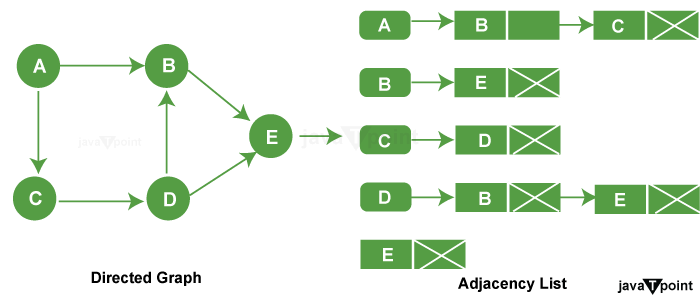
Method 1: Using an Array of Lists (or vectors)

Let's take an example to understand the adjacency list using an array of lists in C++.

#include <iostream>
#include <vector>
class DirectedGraph {
private:
 int numVertices;
 std::vector<std::vector<int>> adjacencyList;
public:
 DirectedGraph(int vertices) {
 numVertices = vertices;
 adjacencyList.resize(vertices);
 }
 void addEdge(int src, int dest) {
 // Adding directed edge from src to dest
 adjacencyList[src].push_back(dest);
 }
 void printGraph() {
 for (int i = 0; i < numVertices; ++i) {
 std::cout << "Vertex " << i << " has outgoing edges to: ";
 for (int neighbor : adjacencyList[i]) {
 std::cout << neighbor << " ";
 }
 std::cout << "\n";
 }
 }
};
int main() {
 DirectedGraph graph(5);
 graph.addEdge(0, 1);
 graph.addEdge(0, 3);
 graph.addEdge(1, 2);
 graph.addEdge(2, 3);
 graph.addEdge(2, 4);
 graph.addEdge(3, 4);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 has outgoing edges to: 1 3 
Vertex 1 has outgoing edges to: 2 
Vertex 2 has outgoing edges to: 3 4 
Vertex 3 has outgoing edges to: 4 
Vertex 4 has outgoing edges to:

Explanation:

In this example, the DirectedGraph class uses an array of vectors to create the adjacency list. The addEdge function adds directed edges from the source vertex to the destination vertex. The printGraph function displays the adjacency list for each vertex.
The arrows indicate the direction of the edges.
The numbers inside the vertices correspond to the vertex numbers.
Each vertex points to its outgoing neighbors.
It represents a directed graph with directed edges going from the source vertex to the destination vertex.

Directed Graph Visualization:

0 --> 1

| |

v v

3 --> 2 --> 4

Explanation:

The code defines a directed graph class that models a directed graph using an adjacency list.
The class has a private member variable, numVertices, to store the number of vertices and an adjacency list to store the adjacency list.
The constructor initializes the numVertices and resizes the adjacency list vector to match the number of vertices.
The addEdge method adds directed edges to the graph by pushing the destination vertex into the vector corresponding to the source vertex in the adjacency list.
The printGraph method prints the adjacency list representation. It iterates through each vertex, printing its outgoing neighbors.
In the main function, an instance of DirectedGraph named graph with 5 vertices is created.
Various edges are added to the graph using the addEdge method, defining the directed relationships.
Finally, the printGraph method is called to display the adjacency list representation of the directed graph.
The program's result is the output that shows the adjacency list of the directed graph, indicating which vertices each vertex is connected.

Complexity Analysis:

Time Complexity:

Constructor (DirectedGraph): O(V), where V is the number of vertices.

addEdge Function: O(1), as adding an edge involves appending to the adjacency list of a vertex.

printGraph Function: O(V + E), where V is the number of vertices and E is the number of edges. It is because it iterates through each vertex and its neighbors.

Main Function: O(E), where E is the number of edges since we add edges in the main function.

Space Complexity:

Constructor (DirectedGraph): O(V + E), as it initializes the adjacencyList vector and each vector inside it for the edges.

addEdge Function: O(1) per edge, as it only appends elements to vectors.

printGraph Function: O(V + E), due to the storage of the adjacency list and its vectors.

Main Function: O(V + E) involves creating the graph object and adding edges.

Where:

V is the number of vertices.

E is the number of edges in the graph.

Method 2: Using Map from Vertices to Neighbors

Let's take an example to understand the adjacency list using the map from vertices to neighbors in C++.

#include <iostream>
#include <map>
#include <vector>
class DirectedGraph {
private:
 int numVertices;
 std::map<int, std::vector<int>> adjacencyList;
public:
 DirectedGraph(int vertices) {
 numVertices = vertices;
 }
 void addEdge(int src, int dest) {
 // Adding directed edge from src to dest
 adjacencyList[src].push_back(dest);
 }
 void printGraph() {
 for (const auto& vertex : adjacencyList) {
 std::cout << "Vertex " << vertex.first << " has outgoing edges to: ";
 for (int neighbor : vertex.second) {
 std::cout << neighbor << " ";
 }
 std::cout << "\n";
 }
 }
};
int main() {
 DirectedGraph graph(5);
 graph.addEdge(0, 1);
 graph.addEdge(0, 3);
 graph.addEdge(1, 2);
 graph.addEdge(2, 3);
 graph.addEdge(2, 4);
 graph.addEdge(3, 4);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 has outgoing edges to: 1 3 
Vertex 1 has outgoing edges to: 2 
Vertex 2 has outgoing edges to: 3 4 
Vertex 3 has outgoing edges to: 4

Here's a visual representation of the directed graph using a map from vertices to neighbors:

Directed Graph Visualization:

Vertex 0 --> [1] Vertex 1 --> [2]

| |

v v

Vertex 3 --> [4] Vertex 2 --> [3, 4]

Vertex 4 --> []

Explanation:

In this example, the code defines a directed graph class that represents a directed graph using a map from vertices to their neighboring vertices. The map is stored as a private member variable named adjacencyList.
The constructor initializes the number of vertices.
The addEdge function adds a directed edge from the source vertex to the destination vertex by appending the destination to the vector associated with the source vertex key in the adjacency list map.
The printGraph function prints the adjacency list representation of the graph by iterating through the map and displaying the outgoing edges for each vertex.
In the main function, a DirectedGraph object named graph is created with 5 vertices. Edges are added to the graph using addEdge to create the directed graph structure.
After that, the printGraph function is called to display the adjacency list representation of the graph, showing which vertices each vertex point is connected to.

Complexity Analysis:

Time Complexity:

Constructor (DirectedGraph): O(V), where V is the number of vertices.

addEdge Function: O(1), as adding an edge involves appending to the adjacency list of a vertex.

printGraph Function: O(V + E), where V is the number of vertices and E is the number of edges. It is because it iterates through each vertex and its neighbors.

Main Function: O(E), where E is the number of edges since we add edges in the main function.

Space Complexity:

Constructor (DirectedGraph): O(V), as it initializes the adjacencyList map to store vertex mappings.

addEdge Function: O(E), where E is the number of edges in the graph, as we store all edges in the adjacency list.

printGraph Function: O(V + E), due to the storage of the adjacency list and its vectors.

Main Function: O(V + E) involves creating the graph object and adding edges.

Where:

V is the number of vertices.

E is the number of edges in the graph.

Undirected Graphs:

An undirected graph is a fundamental concept in graph theory that represents a collection of vertices (nodes) and edges (connections) where the edges do not have a specific direction. In other words, the relationships between vertices are symmetric - if an edge connects vertex A to vertex B, it also implies an edge from vertex B to vertex A.

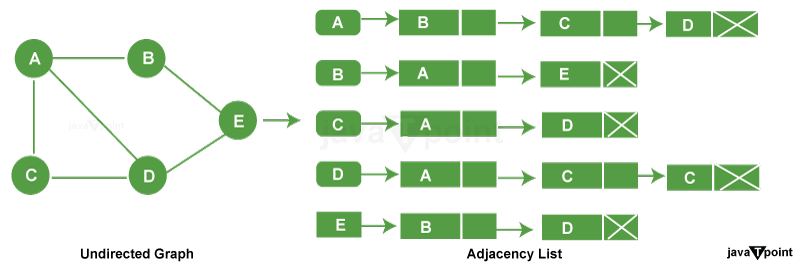
Method-1: Using an Array of Lists (or vectors)

Let's take an example to understand the adjacency list using an array of lists in C++.

#include <iostream>
#include <vector>
class UndirectedGraph {
private:
 int numVertices;
 std::vector<std::vector<int>> adjacencyList;
public:
 UndirectedGraph(int vertices) {
 numVertices = vertices;
 adjacencyList.resize(vertices);
 }
 void addEdge(int src, int dest) {
 // Adding undirected edge between src and dest
 adjacencyList[src].push_back(dest);
 adjacencyList[dest].push_back(src);
 }
 void printGraph() {
 for (int i = 0; i < numVertices; ++i) {
 std::cout << "Vertex " << i << " is connected to: ";
 for (int neighbor : adjacencyList[i]) {
 std::cout << neighbor << " ";
 }
 std::cout << "\n";
 }
 }
};
int main() {
 UndirectedGraph graph(5);
 graph.addEdge(0, 1);
 graph.addEdge(0, 3);
 graph.addEdge(1, 2);
 graph.addEdge(2, 3);
 graph.addEdge(2, 4);
 graph.addEdge(3, 4);
 graph.printGraph();
 return 0;
}

Output

0 is connected to: 1 3 
Vertex 1 is connected to: 0 2 
Vertex 2 is connected to: 1 3 4 
Vertex 3 is connected to: 0 2 4 
Vertex 4 is connected to: 2 3

Each number represents a vertex.

The lines between vertices represent edges.

The graph is undirected, so edges indicate mutual connections between vertices.

Explanation:

In this example, the code defines a class UndirectedGraph that represents an undirected graph using an adjacency list.
The class has a private member numVertices to store the number of vertices and an adjacency list to store the adjacency list.
The constructor initializes numVertices and resizes the adjacency list vector to match the number of vertices.
The addEdge method adds an undirected edge between two vertices by updating their adjacency lists.
The printGraph method iterates through vertices and prints their neighbors, displaying the adjacency list.
An instance of UndirectedGraph named graph with 5 vertices is created in the main function.
Edges are added using the addEdge method to create the connections in the undirected graph.
The printGraph method is called to display the adjacency list representation of the graph.

Complexity Analysis:

Time Complexity:

Constructor (UndirectedGraph): O(V), where V is the number of vertices.

addEdge Function: O(1), as adding an edge involves appending to the adjacency lists of two vertices.

printGraph Function: O(V + E), where V is the number of vertices and E is the number of edges. It is because it iterates through each vertex and its neighbors.

Main Function: O(E), where E is the number of edges since we add edges in the main function.

Space Complexity:

Constructor (UndirectedGraph): O(V), as it resizes the adjacency list vector to match the number of vertices.

addEdge Function: O(1) per edge, as it only appends elements to vectors.

printGraph Function: O(V + E), due to the storage of the adjacency list.

Main Function: O(V + E) involves creating the graph object and adding edges.

Where:

V is the number of vertices.

E is the number of edges in the graph.

Method 2: Using an Array of Deques

We represent an undirected graph using an array of deques (double-ended queues), where each deque contains integers. The integers within each deque represent neighboring vertices that share an edge with the current vertex. This representation is suitable for undirected graphs, where edges have no direction and connect vertices in both directions.

#include <iostream>
#include <deque>
class UndirectedGraph {
private:
 int numVertices;
 std::deque<int>* adjacencyList;
public:
 UndirectedGraph(int vertices) {
 numVertices = vertices;
 adjacencyList = new std::deque<int>[vertices];
 }
 void addEdge(int src, int dest) {
 adjacencyList[src].push_back(dest);
 adjacencyList[dest].push_back(src); // For undirected graphs
 }
 void printGraph() {
 for (int i = 0; i < numVertices; ++i) {
 std::cout << "Vertex " << i << " is connected to: ";
 for (int neighbor : adjacencyList[i]) {
 std::cout << neighbor << " ";
 }
 std::cout << "\n";
 }
 }
 ~UndirectedGraph() {
 delete[] adjacencyList;
 }
};
int main() {
 UndirectedGraph graph(5);
 graph.addEdge(0, 1);
 graph.addEdge(0, 3);
 graph.addEdge(1, 2);
 graph.addEdge(2, 3);
 graph.addEdge(2, 4);
 graph.addEdge(3, 4);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 is connected to: 1 3 
Vertex 1 is connected to: 0 2 
Vertex 2 is connected to: 1 3 4 
Vertex 3 is connected to: 0 2 4 
Vertex 4 is connected to: 2 3

Explanation:

In this example, the code defines a class named UndirectedGraph to represent an undirected graph.
The class includes a private member variable, numVertices, to store the number of vertices in the graph.
The adjacency list is implemented as an array of deques (double-ended queues), where each deque represents a vertex in the graph.
The class constructor takes the number of vertices as a parameter and initializes the numVertices variable.
It dynamically allocates memory for an array of deques, each corresponding to a vertex in the graph.
The addEdge method allows an undirected edge between two vertices (src and dest).
It pushes integers into the deque associated with the source and destination vertices. This operation ensures the graph is undirected, adding the edge in both directions.
The printGraph method is used to display the adjacency list representation of the graph.
It iterates through each vertex in the graph (from 0 to numVertices - 1) and prints the neighbors stored in the associated deque.
The class includes a destructor to release the dynamically allocated memory for the array of deques when the object is destroyed.
In the main function, an instance of the UndirectedGraph class is created with 5 vertices.
Several edges are added to the graph using the addEdge method to establish connections between vertices.
Finally, the printGraph method displays the adjacency list representation of the undirected graph.

Complexity Analysis:

Time Complexity:

The time complexity for creating an array of deques is O(V), where V is the number of vertices.
After that, pushing an integer into a deque takes constant time, O(1).
Adding an edge between two vertices (src and dest) results in two constant-time operations (one for each direction) for undirected graphs.
If there are E edges, the total time complexity for adding edges is O(E).
The method iterates through each vertex (V) and its neighbors (E), resulting in a time complexity of O(V + E).
Deleting the array of deques takes O(V) time complexity.
Overall, the time complexity is dominated by adding edges and printing the graph, making it O(V + E).

Space Complexity:

The space complexity of the array of deques is O(V), where V is the number of vertices.
Two integers (representing neighbors) are stored for each edge, one in each direction for undirected graphs.
If there are E edges, the space complexity for storing integers is O(2E), which simplifies to O(E).
The total space complexity is the sum of the space used by the array of deques and the integers within them, which is O(V + E).

Method-3: Using Map from Vertices to Neighbors

Here's an example of how you can represent an undirected graph using a map from vertices to their neighbors in C++:

#include <iostream>
#include <map>
#include <set>
class UndirectedGraph {
private:
 std::map<int, std::set<int>> adjacencyList;

public:
 void addEdge(int src, int dest) {
 // Adding undirected edge between src and dest
 adjacencyList[src].insert(dest);
 adjacencyList[dest].insert(src);
 }
 void printGraph() {
 for (const auto& vertex : adjacencyList) {
 std::cout << "Vertex " << vertex.first << " is connected to: ";
 for (int neighbor : vertex.second) {
 std::cout << neighbor << " ";
 }
 std::cout << "\n";
 }
 }
};
int main() {
 UndirectedGraph graph;
 graph.addEdge(0, 1);
 graph.addEdge(0, 3);
 graph.addEdge(1, 2);
 graph.addEdge(2, 3);
 graph.addEdge(2, 4);
 graph.addEdge(3, 4);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 is connected to: 1 3 
Vertex 1 is connected to: 0 2 
Vertex 2 is connected to: 1 3 4 
Vertex 3 is connected to: 0 2 4 
Vertex 4 is connected to: 2 3

Explanation:

In this example, the code defines a class named UndirectedGraph that represents an undirected graph using a map from vertices to their neighbors. It also uses the C++ standard library's std::set to store neighbors in sorted order.
The addEdge method in the UndirectedGraph class adds undirected edges to the graph. It takes two vertex indices, src and dest, and adds both vertices to each other's adjacency lists using std::set to ensure that neighbors are stored in sorted order. This way, the same edge is not added multiple times.
The printGraph method is used to print the adjacency list of the graph. It iterates through each vertex in the adjacency list (adjacency list) and prints the neighbors associated with each vertex.
An instance of the UndirectedGraph class named graph is created.
Several undirected edges are added to the graph using the addEdge method.
The printGraph method is called to display the adjacency list representation of the graph.
The code focuses on maintaining a clean adjacency list representation for an undirected graph using a map and sorted sets of neighbors.

Complexity Analysis:

Time Complexity:

Inserting elements into a std::set takes O(log N), where N is the number of neighbors for a vertex. Since each edge involves adding two vertices to their respective sets, the total time complexity for adding all edges would be O(E * log V), where E is the number of edges and V is the number of vertices.
This function iterates through each vertex in the adjacency list and its associated neighbors, which takes O(V + E) time, where V is the number of vertices and E is the number of edges.
Adding edges takes O(E * log V) time.

Space Complexity:

The storage of the adjacency list and sets determine the space complexity:

The space required for the adjacency list is O(V + E), where V is the number of vertices and E is the number of edges.
Each set of neighbors uses O(N) space, where N is the average number of neighbors for each vertex.
Overall space complexity is O(V + E + V * N), which simplifies to O(V + E) if the average number of neighbors is not significantly larger than the number of vertices.

Weighted Graph:

A weighted graph is a type of graph in which each edge has a numerical value associated with it, known as a "weight". This weight represents a quantitative measure of some property, cost, distance, or value associated with the connection between the two vertices that the edge connects. In other words, the weight assigned to an edge provides additional information about the relationship between the vertices it connects.

In a weighted graph:

Each edge has an associated weight representing various quantities such as distance, cost, time, capacity, or any other relevant measure.
The weights can be positive, negative, or zero, depending on the context and the meaning of the weight.
Weighted graphs are used to model scenarios where the relationships between nodes have varying levels of significance, cost, or impact.

For example, consider a scenario where vertices represent cities and edges represent roads between them. In this case, the weights on the edges could represent distances between cities. Similarly, weights represent transaction amounts between accounts in a financial network. Weighted graphs are versatile and find applications in various domains, such as transportation, social networks, network routing, and resource allocation.

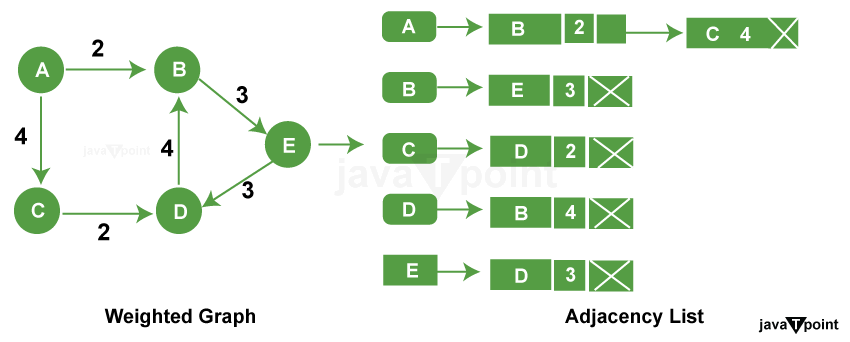
Method-1: Using an Array of Lists (or vectors)

Here's an example of how you can represent a weighted graph using an array of vectors to store the adjacency list in C++:

#include <iostream>
#include <vector>
class WeightedGraph {
private:
 int numVertices;
 std::vector<std::vector<std::pair<int, int>>> adjacencyList;
public:
 WeightedGraph(int vertices) {
 numVertices = vertices;
 adjacencyList.resize(vertices);
 }
 void addEdge(int src, int dest, int weight) {
 // Adding weighted edge from src to dest with a given weight
 adjacencyList[src].emplace_back(dest, weight);
 // Uncomment the line below for an undirected graph
 // adjacencyList[dest].emplace_back(src, weight);
 }
 void printGraph() {
 for (int i = 0; i < numVertices; ++i) {
 std::cout << "Vertex " << i << " is connected to: ";
 for (const auto& neighbor : adjacencyList[i]) {
 std::cout << neighbor.first << " (Weight: " << neighbor.second << ") ";
 }
 std::cout << "\n";
 }
 }
};
int main() {
 WeightedGraph graph(5);
 graph.addEdge(0, 1, 2);
 graph.addEdge(0, 3, 5);
 graph.addEdge(1, 2, 3);
 graph.addEdge(2, 3, 1);
 graph.addEdge(2, 4, 4);
 graph.addEdge(3, 4, 6);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 is connected to: 1 (Weight: 2) 3 (Weight: 5) 
Vertex 1 is connected to: 2 (Weight: 3) 
Vertex 2 is connected to: 3 (Weight: 1) 4 (Weight: 4) 
Vertex 3 is connected to: 4 (Weight: 6) 
Vertex 4 is connected to:

Explanation:

In this example, the code defines a class named WeightedGraph that represents a weighted graph using an array of vectors to store the adjacency list. Each element of the adjacency list is a vector containing pairs representing the destination vertex and the weight of the edge.
The constructor initializes the number of vertices and resizes the adjacency list vector accordingly.
The addEdge method allows adding weighted edges to the graph. It takes the source vertex, destination vertex, and weight as input. The method appends a pair containing the destination vertex and weight to the vector at the source vertex's position in the adjacency list. Additionally, we can uncomment the corresponding line to add the reverse edge for an undirected graph.
The printGraph method is used to display the adjacency list representation of the graph. It iterates through each vertex and its associated neighbors (pairs) in the adjacency list and prints the destination vertex along with the weight of the edge.
An instance of the WeightedGraph class named graph is created in the main function. Several weighted edges are added to the graph using the addEdge method. After that, the printGraph method is called to display the adjacency list representation of the graph, showing the connections between vertices and the associated edge weights.
This code demonstrates how to represent a weighted graph using an array of vectors and incorporate edge weights into the graph structure.

Complexity Analysis:

Time Complexity:

Adding an edge involves appending to the adjacency list of the source vertex, which takes O(1) time.
This function iterates through each vertex in the adjacency list and its associated neighbors (pairs), resulting in a time complexity of O(V + E), where V is the number of vertices and E is the number of edges.
Adding edges using the addEdge method takes O(E) time.

Space Complexity:

The space complexity is determined by the storage of the adjacency list and the pairs representing edges:

The space required for the adjacency list is O(V + E), where V is the number of vertices and E is the number of edges.
Each pair representing an edge uses O(1) space.
Overall space complexity is O(V + E) due to the adjacency list and the pairs.

Where:

V is the number of vertices.

E is the number of edges in the graph.

Method 2: Using Map from Vertices to Neighbors

Here's an example of how you can represent a weighted graph using a map from vertices to their neighbors, where each neighbor is associated with a weight:

#include <iostream>
#include <map>
class WeightedGraph {
private:
 std::map<int, std::map<int, int>> adjacencyList;
public:
 void addEdge(int src, int dest, int weight) {
 // Adding weighted edge from src to dest with a given weight
 adjacencyList[src][dest] = weight;
 // Uncomment the line below for an undirected graph
 // adjacencyList[dest][src] = weight;
 }
 void printGraph() {
 for (const auto& vertex : adjacencyList) {
 std::cout << "Vertex " << vertex.first << " is connected to: ";
 for (const auto& neighbor : vertex.second) {
 std::cout << neighbor.first << " (Weight: " << neighbor.second << ") ";
 }
 std::cout << "\n";
 }
 }
};
int main() {
 WeightedGraph graph;
 graph.addEdge(0, 1, 2);
 graph.addEdge(0, 3, 5);
 graph.addEdge(1, 2, 3);
 graph.addEdge(2, 3, 1);
 graph.addEdge(2, 4, 4);
 graph.addEdge(3, 4, 6);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 is connected to: 1 (Weight: 2) 3 (Weight: 5) 
Vertex 1 is connected to: 2 (Weight: 3) 
Vertex 2 is connected to: 3 (Weight: 1) 4 (Weight: 4) 
Vertex 3 is connected to: 4 (Weight: 6)

Explanation:

In this example, the code defines a class named WeightedGraph that represents a weighted graph using a map from vertices to neighbors, where each neighbor is associated with a weight.
The addEdge method allows adding weighted edges to the graph. It takes the source vertex, destination vertex, and weight as input. The method updates the inner map associated with the source vertex to include the destination vertex as a neighbor, along with the weight of the edge. You can uncomment the corresponding line to add the reverse edge for an undirected graph.
The printGraph method is used to display the adjacency list representation of the graph. It iterates through each vertex in the outer map and its associated neighbors (inner map) to print the destination vertex and the weight of the edge.

At the main function:

An instance of the WeightedGraph class named graph is created.
Several weighted edges are added to the graph using the addEdge method.
After that, the printGraph method is called to display the adjacency list representation of the graph, showing the connections between vertices and the associated edge weights.

Complexity Analysis:

Time Complexity:

Adding an edge involves updating the inner map associated with the source vertex, which takes O(log N) time, where N is the average number of neighbors for a vertex.
This function iterates through each vertex in the adjacency list and its associated neighbors (inner map), resulting in a time complexity of O(V + E), where V is the number of vertices and E is the number of edges.
Adding edges using the addEdge method takes O(E * log N) time.

Space Complexity:

The space complexity is determined by the storage of the adjacency list and the maps representing edges:

The space required for the adjacency list is O(V + E), where V is the number of vertices and E is the number of edges.
Each inner map associated with a vertex uses O(N) space, where N is the average number of neighbors for a vertex.
Overall space complexity is O(V + E + V * N), which simplifies to O(V + E + E * log N) or simply O(V + E) if N is not significantly larger than the number of vertices.

Method-3: Using an Array of Deques

We represent a weighted graph using an array of deques (double-ended queues) containing pairs of integers. The integers in each pair represent the neighbor vertex and the weight of the edge connecting the current vertex to its neighbor.

#include <iostream>
#include <deque>
class WeightedGraph {
private:
 int numVertices;
 std::deque<std::pair<int, int>>* adjacencyList;
public:
 WeightedGraph(int vertices) {
 numVertices = vertices;
 adjacencyList = new std::deque<std::pair<int, int>>[vertices];
 }
 void addEdge(int src, int dest, int weight) {
 adjacencyList[src].push_back(std::make_pair(dest, weight));
 adjacencyList[dest].push_back(std::make_pair(src, weight)); // For undirected graphs
 }
 void printGraph() {
 for (int i = 0; i < numVertices; ++i) {
 std::cout << "Vertex " << i << " is connected to: ";
 for (const auto& neighbor : adjacencyList[i]) {
 std::cout << neighbor.first << " (Weight: " << neighbor.second << ") ";
 }
 std::cout << "\n";
 }
 }
 ~WeightedGraph() {
 delete[] adjacencyList;
 }
};
int main() {
 WeightedGraph graph(5);
 graph.addEdge(0, 1, 2);
 graph.addEdge(0, 3, 5);
 graph.addEdge(1, 2, 3);
 graph.addEdge(2, 3, 1);
 graph.addEdge(2, 4, 4);
 graph.addEdge(3, 4, 6);
 graph.printGraph();
 return 0;
}

Output

Vertex 0 is connected to: 1 (Weight: 2) 3 (Weight: 5) 
Vertex 1 is connected to: 0 (Weight: 2) 2 (Weight: 3) 
Vertex 2 is connected to: 1 (Weight: 3) 3 (Weight: 1) 4 (Weight: 4) 
Vertex 3 is connected to: 0 (Weight: 5) 2 (Weight: 1) 4 (Weight: 6) 
Vertex 4 is connected to: 2 (Weight: 4) 3 (Weight: 6)

Explanation:

In this example, the code defines a class named weighted graph to represent a weighted graph.
It includes a private member variable, numVertices, to store the number of vertices in the graph.
The class constructor takes the number of vertices as a parameter and initializes the numVertices variable.
It dynamically allocates memory for an array of deques, each corresponding to a vertex in the graph.
The adjacency list is implemented as an array of deques containing pairs of integers. Each pair consists of the neighbor vertex and the weight of the edge connecting the current vertex to that neighbor.
The addEdge method allows adding a weighted edge between two vertices (src and dest) with a specified weight.
It pushes a pair into the deque associated with the source and destination vertices. This pair includes the neighbor vertex (dest) and the edge weight connecting the current vertex (src) to that neighbor.
For undirected graphs, it also adds the reverse edge to ensure symmetric relationships between vertices.
The printGraph method is used to display the adjacency list representation of the graph.
It iterates through each vertex in the graph (from 0 to numVertices - 1) and prints the neighbors and their associated edge weights.
The class includes a destructor to release the dynamically allocated memory for the array of deques when the object is destroyed.
In the main function, an instance of the WeightedGraph class is created, and several weighted edges are added to the graph using the addEdge method. Finally, the printGraph method is called to display the adjacency list representation of the graph, including the vertices, their neighbors, and edge weights.
This code provides a clear and efficient representation of a weighted graph using an array of deques. It is suitable for various applications where weighted edges and efficient neighbor traversal are essential.

Complexity Analysis:

Time Complexity:

The time complexity for creating an array of deques is O(V), where V is the number of vertices.
Pushing a pair into a deque takes constant time, O(1).
Adding an edge between two vertices results in two constant-time operations for undirected graphs.
If there are E edges, the total time complexity for adding edges is O(E).
The method iterates through each vertex and its neighbors, resulting in a time complexity of O(V + E), where V is the number of vertices, and E is the number of edges.
Deleting the array of deques takes O(V).
Therefore, the time complexity is dominated by adding edges and printing the graph, making it O(V + E).

Space Complexity:

The space complexity of the array of deques is O(V), where V is the number of vertices.
A pair (neighbor vertex, edge weight) is stored twice for undirected graphs for each edge.
If there are E edges, the space complexity for storing pairs is O(2E), which simplifies to O(E).
The total space complexity is the sum of the space used by the array of deques and the pairs in the deques, which is O(V + E).

Applications of Adjacency lists:

Adjacency lists are a commonly used representation of graphs due to their efficiency in various applications. Here are some common applications of adjacency lists:

Social Networks: In social networks like Facebook, Twitter, and LinkedIn, each user can be represented as a vertex, and their connections (friendships, followers, etc.) can be represented using adjacency lists.

Recommendation Systems: Many recommendation algorithms suggest items, products, or friends using graph structures. The adjacency list representation helps model relationships and connections between users or items, enabling more accurate recommendations.

Routing and Networks: In computer networks, adjacency lists represent a network's topology. They help find the shortest paths, optimize data routing, and manage network resources efficiently.

Game Development: In video game development, adjacency lists can be used to model game worlds, where vertices represent locations or scenes, and edges represent possible transitions between scenes.

Data Mining and Clustering: In clustering algorithms, adjacency lists can represent similarity relationships between data points. Each vertex represents a data point, and edges represent similarity measures.

Graph Algorithms: Many graph algorithms, such as depth-first search (DFS), breadth-first search (BFS), Dijkstra's algorithm, and Prim's algorithm, work efficiently with the adjacency list representation. This representation allows quick access to neighbors and their associated information.

Benefits:

Memory Efficiency: Adjacency lists are memory-efficient for sparse graphs, as they only store information about existing edges. It makes them suitable for graphs with fewer edges than the maximum possible edges.

Ease of Traversal: Traversing the neighbors of a vertex is straightforward with adjacency lists. Iterating through a vertex's adjacency list takes only as much time as the number of neighbors, making certain graph algorithms more efficient.

Dynamic Graphs: Adjacency lists are well-suited for situations where the graph structure evolves. Adding or removing edges or vertices can be done efficiently without affecting the entire data structure.

Applications with Variable Connectivity: When the degree of connectivity between vertices varies widely, adjacency lists are more efficient regarding memory usage than adjacency matrices.

Limitations:

Space Complexity (Dense Graphs): For dense graphs (with many edges), adjacency lists can have higher space complexity than adjacency matrices. In such cases, they become less memory-efficient.

Neighbor Lookup Time: While adjacency lists are efficient for traversing neighbors, looking up whether two vertices are directly connected (edge existence) takes O(degree) time, where degree is the average number of neighbors.

Edge Weight Retrieval: In weighted graphs, adjacency lists require extra space to store the edge weights. Retrieving edge weights might take additional time due to the need to search for the specific neighbor.

Edge Deletion: Removing an edge from an adjacency list requires searching and potentially resizing the list. This operation might be less efficient than edge deletion in an adjacency matrix.

Graph Representation Trade-off: The choice between adjacency lists and matrices depends on the specific graph characteristics and the type of operations performed. Some algorithms might be more efficient with matrixes due to constant-time edge existence checks.

Next TopicMake_pair in C++

← prev next →