Bubble Sort Algorithm in C++

Introduction to Sorting Algorithms

The skill of sorting is crucial in the large field of computer science, where data is king. The unsung heroes of the digital world, sorting algorithms silently bring order to chaos in the background. They are crucial to many facets of computer science, from data analysis to information retrieval, and it is impossible to emphasize their importance.

Importance of Sorting Algorithms in Programming

1. Information Retrieval:

Sorting enables efficient searches. Consider a scenario where you need to find a particular book in a library with thousands of volumes. Without any organization, you'd need to scour every shelf aimlessly. However, if the books are sorted by author, title, or genre, finding your book becomes a systematic process. Algorithms like binary search rely on sorted data to quickly pinpoint desired information. Imagine searching through an unsorted list of a million items - it would be akin to finding a needle in a haystack.

2. Data Analysis:

Sorting lays the foundation for data analysis. In the world of big data, where information is generated at an astonishing rate, the ability to make sense of data is invaluable. Sorting simplifies tasks like finding the maximum or minimum values, identifying duplicates, or generating statistics. These operations are the building blocks of data-driven decision-making. For instance, when analyzing sales data, sorting can help identify top-selling products or uncover patterns in customer behavior.

3. User Experience:

In user interfaces and web applications, sorted data provides a seamless experience. Think about browsing an e-commerce website. When you search for products, you often want to see them in a particular order - perhaps sorted by price, rating, or relevance. Sorting algorithms ensure a user-friendly interaction by presenting data in a structured and intuitive manner. Without sorting, these platforms would feel chaotic and frustrating to navigate.

4. Optimization:

Sorting is a critical component of many optimization problems. For example, scheduling tasks efficiently, routing vehicles, or allocating resources in a way that minimizes costs often requires arranging data in a specific order. Sorting algorithms provide a means to achieve these optimizations, which have far-reaching impacts on industries ranging from logistics to finance.

Comparison Based Searching

Comparison-based searching, often referred to as comparison-based search algorithms, is a class of algorithms used to find a specific element within a collection of data (such as an array or a list) by comparing elements in the collection with the target element. These algorithms rely on the principle of making comparisons between elements to determine their relative order and ultimately locate the desired item.

Key Concepts:

Comparison Operation: The comparison of components to determine equality or order is at the heart of comparison-based searching. If one element is bigger than, less than, or equal to another element, it can be determined using this comparison process. It serves as a fundamental building piece for algorithms for sorting and searching.
Data collection: The data structure in which you are searching could be an array, list, tree (such as a binary search tree), or any other structure that permits element retrieval and comparison.
Target Element: To locate a particular target element inside the collection is the aim of a comparison-based search. You want to find the element that is the target.

Common Comparison-Based Search Algorithms:

Linear Search (Sequential Search): Linear search is the simplest comparison-based search algorithm. A match is found or the collection's conclusion is reached after going through each element one at a time and comparing it to the target. Although linear search is simple to comprehend and appropriate for unordered lists, it might be ineffective for huge datasets.
Binary Search: Binary search is a highly efficient comparison-based search algorithm that works on sorted collections. It takes advantage of the fact that the data is sorted to divide the search space in half with each comparison. By repeatedly halving the search space, binary search efficiently narrows down the possible locations of the target element until it is found or the search space is exhausted.
Hashing: Hash-based searching relies on hashing functions to map elements to specific locations within a data structure like a hash table. It is a constant-time (O(1)) search operation in the best case when the hash function is well-distributed, making it extremely efficient for searching, but it requires careful management of hash collisions.

Complexity Analysis:

The efficiency of comparison-based search algorithms is often evaluated in terms of time complexity, which represents the number of comparisons or basic operations required to find the target element. In general, the efficiency varies based on the specific algorithm and the characteristics of the data.

Linear Search: O(n) worst-case time complexity, where n is the number of elements in the collection.
Binary Search: O(log?(n)) worst-case time complexity for sorted collections.
Hashing: O(1) average-case time complexity for well-designed hash functions, but it can degrade to O(n) in the worst case if there are many collisions.

Introduction to Bubble Sort Algorithm

Bubble sort is a straightforward and elementary sorting algorithm used to arrange elements in a list or array in ascending or descending order. It belongs to the family of comparison-based sorting algorithms, known for its simplicity but relatively poor performance on large datasets compared to more advanced sorting algorithms like quicksort or merge sort. Despite its inefficiency for large datasets, bubble sort serves as an educational tool for understanding sorting algorithms and their principles.

The fundamental concept behind bubble sort is the repeated comparison and swapping of adjacent elements in the list until the entire list is sorted. The algorithm derives its name from the way smaller elements "bubble" to the top of the list, while larger elements gradually sink to the bottom.

Inefficiency for Larger Datasets:

Comparisons and Swaps: Bubble sort involves repeatedly comparing and swapping adjacent elements in the list until the entire list is sorted. In the worst-case scenario, where the list is in reverse order, bubble sort will require many comparisons and swaps to move the largest elements to their correct positions. As the dataset size increases, the number of these comparisons and swaps grows quadratically.
Nested Loops: Bubble sort employs nested loops to traverse the list and perform comparisons and swaps. Bubble sort performs comparisons and swaps by iterating through each member of the list in the outer loop and the unsorted part of the list in the inner loop. Larger datasets necessitate running both loops more frequently, which significantly raises the number of iterations.
No Early Exit: Bubble sort does not have any mechanism for early exit. This means that even if the list is almost sorted, the algorithm will continue to perform unnecessary comparisons and swaps. In contrast, more efficient sorting algorithms like quicksort can exit early when they detect that the list is already mostly sorted, reducing the number of operations.
Quadratic Time Complexity: The time complexity of bubble sort is O(n^2) in the worst and average cases, where "n" is the number of elements in the list. This quadratic growth rate makes bubble sort impractical for large datasets. As "n" becomes large, the time required to sort the data can become prohibitively long.

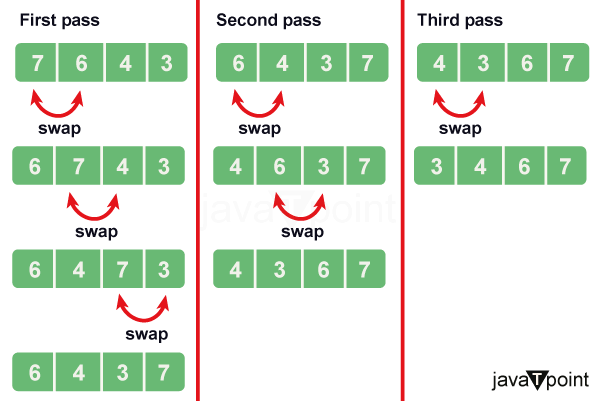
Working of Bubble Sort Algorithm

Bubble Sort is a simple and intuitive sorting algorithm that operates by repeatedly stepping through a list or array of elements and comparing adjacent pairs. If two adjacent elements are out of order, the algorithm swaps them. This process is repeated until no more swaps are needed, indicating that the list is fully sorted.

Initialization:
- Begin by initializing an index variable that will keep track of the current position in the list. This index starts at the first element (index 0).
Comparison:
- Compare the element at the current index with the element immediately to its right (i.e., the next element in the list).
Comparison Result:
- If the element at the current index is greater than the next element, it means they are out of order, and a swap is needed. If they are in the correct order (current element <= next element), no action is taken.
Swapping:
- Perform the swap of the two elements. This involves temporarily storing the value of the current element, overwriting it with the value of the next element, and then placing the temporarily stored value into the next element's position.
Index Update:
- Increment the index by one to move to the next pair of adjacent elements for the next comparison and, if necessary, a swap.
Pass Completion:
- After completing a pass through the list, the largest unsorted element is guaranteed to have "bubbled up" to the end of the list. The last element in the pass is now in its correct sorted position.
Repeat Until Sorted:
- Repeat steps 1-6 until you can go through the entire list without performing any swaps during a pass. When this happens, it means the entire list is sorted.
Termination:
- Once no swaps are needed during a pass, the algorithm terminates. At this point, the list is fully sorted in ascending order, with the smallest elements at the beginning and the largest elements at the end.

The basic idea remains the same: repeatedly comparing and swapping adjacent elements until the list is sorted.

Code

#include <iostream>
void bubbleSort(int arr[], int n) {
    bool swapped; // A flag to indicate whether any swaps were made in a pass
    for (int i = 0; i < n - 1; i++) {// Outer loop for multiple passes
        swapped = false; // Initialize swapped as false for each pass
        // Inner loop for each pass through the array
        for (int j = 0; j < n - i - 1; j++) {
            // Compare adjacent elements
            if (arr[j] > arr[j + 1]) {
                // Swap arr[j] and arr[j+1] if they are in the wrong order
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swapped = true; // Set swapped to true to indicate a swap occurred
            }
        }
        // If no two elements were swapped in the inner loop, the array is sorted
        if (!swapped) {
            break;
        }
    }
}
int main() {
    int arr[] = {64, 25, 12, 22, 11};
    int n = sizeof(arr) / sizeof(arr[0]);
    std::cout << "Original Array: ";
    for (int i = 0; i < n; i++) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
    bubbleSort(arr, n);
    std::cout << "Sorted Array: ";
    for (int i = 0; i < n; i++) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
    return 0;
}

Explanation

The code begins by including the necessary input-output library, <iostream>, and declaring a bubbleSort function to perform the sorting. Within the bubbleSort function, there's a flag named swapped used to track whether any swaps were made during a pass through the array. The code employs two nested loops, where the outer loop controls multiple passes through the array, and the inner loop iterates through the elements in each pass, comparing adjacent elements and swapping them if they are out of order. If no swaps are made in a pass, it breaks out of the outer loop, as the array is considered sorted. The main function initializes an array, prints the original unsorted array, calls the bubbleSort function to sort it, and finally prints the sorted array. This code provides a clear demonstration of the Bubble Sort algorithm in action, making it easier to understand the mechanics of this sorting technique.

Applications of Bubble Sort

Educational Purposes: Bubble sort is often used as an educational tool to teach fundamental sorting concepts in computer science. It's a straightforward algorithm that helps beginners understand the basic principles of sorting, such as comparisons, swaps, and iteration. Students can implement and experiment with bubble sort as a starting point before moving on to more advanced sorting algorithms.
Small Datasets and Simple Tasks: Bubble sort is suitable for sorting small datasets or lists where efficiency is not a primary concern. If you have a list with just a few elements that need to be sorted, bubble sort can be a quick and easy solution to implement. It's especially handy for simple tasks like sorting names, scores, or other small sets of data in casual applications.
Debugging and Validation: Bubble sort can be used as a debugging tool to verify whether an array is sorted correctly or to identify adjacent elements that are out of order. Developers can use bubble sort to quickly check if their sorting logic is working as expected before implementing more efficient sorting algorithms in production code.
Prototyping and Proof of Concept: Efficiency may be sacrificed in favor of simplicity and speed of implementation when creating software prototypes or proof-of-concept projects. In these situations, bubble sort might be utilized as an interim sorting method to get a project up and running as soon as possible. More effective sorting algorithms can be incorporated after the prototype has been proven.
Historical Significance: Bubble sort has historical significance as one of the earliest sorting algorithms. Learning about bubble sort can help computer scientists and developers appreciate the evolution of sorting algorithms over time. Understanding its limitations and inefficiencies is valuable for gaining insights into algorithm design and optimization.
Interactive Demonstrations: Bubble sort can be used in educational software, simulations, or websites to visually demonstrate sorting algorithms. It can provide an interactive and engaging way to teach sorting concepts to students or users. Animated visualizations of bubble sort can make the learning process more intuitive.
Comparative Testing: Bubble sort can be used for comparative testing of other sorting algorithms. It can serve as a reference implementation to verify the correctness of more efficient sorting algorithms. By comparing the results of bubble sort with other algorithms, developers can identify discrepancies and potential issues.