C++ hashing programme with chaining

What exactly is hash table chaining?

Chaining is a hash table collision avoidance technique.

A collision occurs when two keys in a hash table are hashed to the same index. Collisions are an issue because each slot in a hash table is only supposed to hold one element.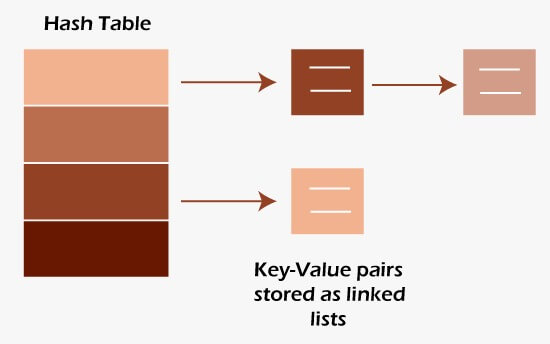

The chaining method

The hash table in the chaining approach is an array of linked lists, with each index having its own linked list.

All key-value pairs that map to the same index will be stored in that index's linked list.

The Advantages of Chaining

• Insertion in a hash table always occurs in O(1) through chaining because linked lists allow insertion in constant time.
• A chained hash table can theoretically grow indefinitely as long as there is enough space.
• A chained hash table will never need to be resized.

Implementation of Chaining

Let's write a hash function to ensure that our hash table has 'N' buckets.

To add a node to the hash table, we must first determine the hash index for the given key. It could also be computed using the hash function.

Example: hashIndex = key % noOfBuckets

Insert: Move to the bucket that corresponds to the hash index calculated above and insert the new node at the end of the list.

Delete: To delete a node from a hash table, calculate the hash index for the key, move to the bucket corresponding to the calculated hash index, search the list in the current bucket for the node with the given key, and remove it (if found).

Algorithm

For Insert:

For Delete:

For Search:

Code

Output

1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 2
Enter key at which element to be inserted: 1
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 3
Enter key at which element to be inserted: 4
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 7
Enter key at which element to be inserted: 6
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 1
Enter element to be inserted: 8
Enter key at which element to be inserted: 9
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 2
Enter key of the element to be searched: 6
Element found at key 6: 7
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 2
Enter key of the element to be searched: 7
No Element found at key 7
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. Exit
Enter your choice: 3
Enter key of the element to be deleted: 9
Element Deleted
1. Insert element into the table
2. Search element from the key
3. Delete element at a key
4. ExitC
Enter your choice: 4

Time Complexity:

• Search : O (1+(n/m))
• Delete : O (1+(n/m))
• where n = Number of slots in Hash table
  m = Number of keys to be inserted
  Here n/m is the Load Factor.
• Load Factor must be as small as possible.