Babylonian Square Root Algorithm in C++
In this article, we will discuss the Babylonian square root algorithm in C++ with its history and examples.
Introduction:
The Babylonian square root algorithm, also known as Heron's method, is an iterative method to approximate the square root of a given number. It is based on the idea of repeatedly averaging an initial guess with the original number divided by the guess. The algorithm converges quickly to the actual square root. The algorithm dates back to the Babylonian civilization and is named after the ancient Greek mathematician Heron of Alexandria, who described it in his work "Metrica" around 100 AD.
The algorithm is based on the principle of successive approximations. Given a positive number N, the algorithm starts with an initial guess x0 (which could be any reasonable starting point, often N/2 or 1), and iteratively refines the estimate using the formula:
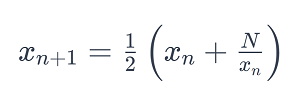
History:
The Babylonian square root algorithm, also known as Heron's method, has a rich historical background that dates back to ancient civilizations. It is named after the ancient Greek mathematician Heron of Alexandria, but its origins can be traced even further back to the Babylonians.
- Babylonian Civilization (circa 2000-1600 BCE): The Babylonians are credited with some of the earliest mathematical developments in human history. Their mathematical clay tablets reveal that they had methods for approximating square roots. They used geometric shapes and applied numerical methods to solve mathematical problems, including square roots.
- Heron of Alexandria (circa 10-70 AD): Heron, a Greek mathematician and engineer, described the square root extraction method in his work "Metrica" around 100 AD. His version of the algorithm was applied to find square roots and cube roots geometrically.
- Islamic Golden Age (8th-14th centuries): During the Islamic Golden Age, scholars from the Islamic world further developed and refined mathematical techniques. They translated Greek and Roman mathematical texts, including Heron's work, and contributed to the understanding and application of mathematical methods.
- Renaissance and Later Periods: Heron's method was rediscovered during the Renaissance and later periods in Europe. Mathematicians like François Viète and John Wallis studied and extended the algorithm. It became a fundamental technique in the broader context of numerical analysis.
- Modern Usage: The Babylonian square root algorithm remains a foundational method for approximating square roots and is still used in various forms today. Iterative methods for numerical analysis, including the Newton-Raphson method (which is a generalization of Heron's method), draw inspiration from this ancient algorithm.
Program 1:
Let us take an example to illustrate the use of the Babylonian square root algorithm in C++:
Output:
Enter a number to find its square root: 25
Square root of 25 is approximately: 5
Explanation:
1. Initialization: Choose an initial guess (x0) for the square root. It can be any reasonable starting point, but common choices include x0 = N/2 or x0 =1, where N is the number for which you want to find the square root.
2. Iteration:
- For each iteration (n), calculate the next approximation using the formula:
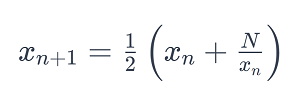
- This formula combines the current guess xn with the ratio N/xn to produce a new estimate that, on average, is closer to the actual square root.
3. Convergence Check:
- Check the difference between consecutive approximations. The iteration continues until the difference is sufficiently small. The criterion for stopping the iteration is typically based on a specified tolerance level (epsilon, ε):
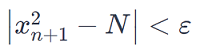
4. Termination:
- Once the convergence criterion is met, terminate the iteration. The last obtained value (x n+1) is considered an approximation of the square root of N.
Program 2:
Let us take another example to illustrate the use of the Babylonian square root algorithm in C++:
Output:
Enter a number to find its square root: 64
Square root of 64 is approximately: 8
Explanation:
1. Header Files:
- The code includes two standard C++ header files: <iostream> for input and output operations and <cmath> for mathematical functions.
2. Babylonian Square Root Function:
- The function babylonianSquareRoot is defined to calculate the square root using the Babylonian method.
- It takes two parameters: n (the number for which the square root is to be calculated) and epsilon (a small positive value to control the precision of the result).
- The function checks if the input n is less than 0, in which case it prints an error message and returns a specified error code or throws an exception.
- If n is 0, it returns 0, as the square root of 0 is 0.
- The function initializes a variable guess as the initial guess (typically set to n / 2.0).
3. Do-While Loop:
- The core of the algorithm is a do-while loop, which continues until the convergence criterion is met.
- Inside the loop, a new guess (newGuess) is calculated using the Babylonian formula.
- The loop checks if the absolute difference between the new guess and the old guess is less than the specified epsilon. If true, it breaks out of the loop, indicating convergence.
- If not, the new guess becomes the current guess, and the loop continues.
4. Main Function:
- The main function is the entry point of the program.
- It prompts the user to enter a number and reads the input into the variable number.
- After that, it calls the babylonianSquareRoot function with the entered number, obtaining the result.
- If the result is not equal to the specified error code (-1.0), it prints the calculated square root.
- Return 0: The main function returns 0, indicating successful program execution.
Time and Space complexities:
Time Complexity:
- The number of iterations required for convergence primarily determines the time complexity of the Babylonian square root algorithm.
- Let k be the number of iterations needed for convergence, and ? be the tolerance level.
Time Complexity: The algorithm exhibits a logarithmic convergence behavior, and the number of iterations is usually relatively small and proportional to the precision required. Therefore, the time complexity is often considered as O(log( 1/? )).
In practical terms, the algorithm often converges in a fixed number of iterations, making it efficient.
Space Complexity:
- The space complexity of the algorithm is related to the storage of variables and the stack space used during the function calls.
Space Complexity: The algorithm uses a constant amount of space for variables, regardless of the input size. Therefore, the space complexity is considered as O(1), indicating constant space usage.
The space required for the variables (e.g., guess, newGuess, number, etc.) remains constant, and additional space is not dependent on the input size.
Advantages of the Babylonian square root algorithm:
There are several advantages of the Babylonian square root algorithm in C++. Some main advantages of the Babylonian square root algorithm in C++:
- Fast Convergence: The algorithm converges rapidly, meaning that it approaches the actual square root with each iteration. It leads to quick and efficient approximations.
- Simplicity: The algorithm is straightforward and easy to understand. Its simplicity makes it an attractive choice for square root approximation, especially in educational contexts or applications where computational efficiency is not the primary concern.
- Low Computational Complexity: The algorithm involves basic arithmetic operations (addition, division, and multiplication), which have relatively low computational complexity. It makes it computationally efficient, especially when compared to more complex numerical methods.
- Applicability to Various Contexts: The Babylonian square root algorithm is applicable to a wide range of contexts, including hand calculations, programming environments, and embedded systems. Its versatility makes it suitable for various applications.
- Numerical Stability: The algorithm is numerically stable, and small variations in the input value or initial guess do not usually lead to divergent behavior. This stability is important in numerical methods to ensure reliable and consistent results.
- Historical Significance: The algorithm has historical significance, dating back to ancient civilizations. Its enduring use highlights its effectiveness and importance in the development of numerical methods throughout history.
Applications of the Babylonian square root algorithm:
There are several applications of the Babylonian square root algorithm in C++. Some main applications of the Babylonian square root algorithm in C++:
- Numerical Analysis: The algorithm is a fundamental component of numerical analysis, providing a simple and effective method for approximating square roots. It is often used as a starting point for more complex algorithms.
- Computer Programming: The Babylonian square root algorithm is commonly implemented in programming languages to calculate square roots. Many programming environments, including scientific and engineering applications, use this algorithm due to its simplicity and quick convergence.
- Calculator Implementations: The algorithm is used in the software of calculators to efficiently compute square roots. Its rapid convergence makes it suitable for real-time applications, providing users with quick and accurate results.
- Embedded Systems: In resource-constrained environments, such as embedded systems in electronic devices, the Babylonian square root algorithm can be preferred due to its low computational complexity and ease of implementation.
- Education: The algorithm is often used in educational settings to teach the concept of iterative methods for approximating mathematical functions. Its simplicity makes it accessible for students studying numerical methods.
- Financial Calculations: The algorithm can be used in financial calculations where quick approximations of square roots are needed. For example, it might be applied in risk assessments or option pricing models.
- Signal Processing: In some signal processing applications, where real-time calculations are crucial, the Babylonian square root algorithm can be employed for its efficiency in approximating square roots.
- Scientific Research: The algorithm is used in various scientific disciplines for quick and practical approximations. It is particularly valuable when high precision is not critical, and computational efficiency is essential.
While the Babylonian square root algorithm is versatile, it's important to note that in certain applications requiring very high precision or specific error analysis, more advanced algorithms like Newton's method might be preferred. Additionally, its historical significance and simplicity make it an interesting subject of study in the context of numerical methods.
Significance of The Babylonian square root algorithm in computer programming:
The Babylonian square root algorithm holds significant importance in computer programming due to its simplicity, efficiency, and widespread applicability. Its straightforward nature makes it an accessible choice for programmers at all skill levels, contributing to its adoption in various software applications. The algorithm strikes a balance between accuracy and speed, making it computationally efficient for a broad range of scenarios where square root calculations are required. Its common use case in programming, ranging from basic arithmetic to complex mathematical computations, underscores its practicality and versatility.
One of the algorithm's notable strengths lies in its numerical stability, ensuring consistent and reliable results even in the presence of small variations in input or initial guesses. This stability is a crucial attribute in programming, where robust and predictable behaviour is essential. Additionally, the historical continuity of the Babylonian square root algorithm adds to its significance. Originating from ancient civilizations, its enduring effectiveness has led to its continued use in modern computer programming.
In environments with resource constraints, such as embedded systems, the algorithm's relatively low computational complexity makes it a suitable choice. Its efficiency contributes to its popularity in scenarios where quick and reasonably accurate square root approximations are required.
Disadvantages of the Babylonian square root algorithm:
There are several disadvantages of the Babylonian square root algorithm in C++. Some main disadvantages of the Babylonian square root algorithm in C++:
- Convergence Rate in Certain Cases: While the algorithm generally converges rapidly, there are cases where the convergence rate might be slower, especially for numbers with peculiar properties or near-zero values. Other methods, like Newton's method, may have faster convergence in some situations.
- Initial Guess Dependency: The performance of the algorithm can be sensitive to the choice of the initial guess. In certain scenarios, a poorly chosen initial guess may lead to slower convergence or divergence. Choosing a good initial guess requires some knowledge of the properties of the input.
- Not Suitable for Negative Numbers: The algorithm is designed for positive real numbers. It cannot be directly applied to find the square root of negative numbers. Handling negative inputs may require additional considerations or a different approach.
- Not Suitable for Complex Numbers: The algorithm is limited to real numbers. If complex roots are needed, other methods specifically designed for complex numbers, such as the Newton-Raphson method for complex functions, would be more appropriate.
- Precision Limitations: The Babylonian algorithm may not be the most suitable choice for applications requiring extremely high precision. Other algorithms, such as iterative methods with higher-order convergence, might be preferred for such scenarios.
- Requires Division Operation: The algorithm involves a division operation in each iteration, which may be computationally expensive on certain platforms. In situations where division operations are costly, alternative methods might be more efficient.
- Handling Near-Zero Values: The algorithm may encounter difficulties when the input is very close to zero. In such cases, issues related to numerical precision and floating-point arithmetic may affect the accuracy of the result.
- Not the Most Efficient for Extreme Precision: For applications requiring extremely high precision, more advanced algorithms, such as specialized square root algorithms or arbitrary-precision arithmetic libraries, may outperform the Babylonian algorithm.
While the Babylonian square root algorithm is versatile and widely used, these disadvantages highlight situations where other algorithms or methods may be more suitable, depending on the specific requirements of an application. Understanding these limitations helps in making informed choices when selecting a square root approximation method.
Other Alternatives:
- Newton's Method (Newton-Raphson Method): Newton's method is an iterative numerical technique for finding roots of real-valued functions. It can be adapted to find square roots. Newton's method tends to converge faster than the Babylonian method, especially for functions with higher-order convergence.
- Binary Search Algorithm: The binary search algorithm can be adapted to find the square root by searching for the square root in a given range. It repeatedly bisects the search interval until the desired precision is achieved. Binary search is efficient but may take more iterations than methods with higher-order convergence.
- Exponential Function and Logarithm: Some mathematical libraries or hardware instructions provide specialized functions for exponentiation and logarithms that can be used to calculate square roots.
- CORDIC Algorithm: The Coordinate Rotation Digital Computer (CORDIC) algorithm is often used for trigonometric and hyperbolic function calculations, but it can be adapted to compute square roots. It uses a series of simple and fixed-point operations, making it suitable for hardware implementation.
Conclusion:
In conclusion, the Babylonian square root algorithm is a simple and effective method for approximating square roots. It has been used for centuries and remains a practical choice due to its ease of implementation and rapid convergence. The algorithm is suitable for a variety of applications, including numerical analysis, programming, and embedded systems.
Key points about the Babylonian square root algorithm:
- Iterative Nature: The algorithm iteratively refines its estimate of the square root, converging rapidly to the actual value.
- Simplicity: Its straightforward formula and minimal computational complexity make it accessible for educational purposes and practical implementations.
- Versatility: The algorithm can be applied to various contexts, ranging from hand calculations to computer programming and embedded systems.
- Competition: While other algorithms, like Newton's method offer faster convergence in some cases, the Babylonian method strikes a balance between simplicity and efficiency.
- Applications: The algorithm provides quick and satisfactory approximations for square roots, and it is widely used in fields such as numerical analysis, programming, and embedded systems.
While the Babylonian method is widely used, it's essential to consider its limitations, such as sensitivity to the initial guess and its suitability for specific precision requirements. In scenarios where higher precision or specialized considerations are needed, alternative algorithms like Newton's method or binary search may be preferred.
The implementation and enhancement of the Babylonian square root algorithm provide valuable insights into numerical methods, error handling, and user interface design. Exploring and understanding different square root algorithms broadens one's understanding of computational techniques and their applications.
In practical terms, the Babylonian square root algorithm remains a fundamental and efficient approach for square root approximation, and its simplicity makes it an accessible topic for learning and exploration in the realm of numerical computing.
|
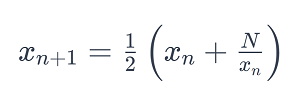
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now