Des in C++

Introduction

A wealth of data was produced with the dawn of the information age. Protecting sensitive information has become increasingly important due to the need to preserve people's privacy. As a result, the way information is protected during transmission over networks and storage in system memory is given a lot more weight.

The DES (Data Encryption Standard) algorithm was developed by IBM. It is a symmetric-key technique based on an older algorithm provided by Horst Feistel in the 1970s with the advent of scientific discipline technologies. Symmetric key algorithms use the same key to encrypt and decrypt both the message and the ciphertext. The American National Bureau of Standards received the algorithm.

Following discussions with the National Security Agency (NSA), a few adjustments were made to the DES algorithm in 1976. This algorithm was then chosen and formally published as a Federal Information Processing Standard (FIPS) in America in 1977.

Describe the DES algorithm.

The Data Encryption Standard algorithm is a block cypher method that uses a 48 bit key for each input and converts 64 bit blocks of plaintext into 64 bit blocks of cypher text at a time. The text that needs to be encrypted is divided up into units called "blocks", and each block is encrypted separately using the key in block cypher techniques.

The encryption process is exactly reversed during the decryption step. Using the same 48 bit key during encryption, it accepts a 64 bit block of ciphertext and outputs a 64 bit block of plaintext. The same key must be used by both the encryptor and the decryptor in order for them to be able to interact.

The DES algorithm was successful in the early days of the internet, but today's applications cannot use it because of its inadequate key length of 56 bits. With the advancement of technology and a rise in processing power, a determined attacker can quickly crack the key with the right tools. However, it has had a significant impact on the growth and development of cryptography.

How to Create a Key

Letters and numerals are not used by computers. Before they are encrypted, all of the plaintext characters are transformed to binary. Data is divided into blocks for processing throughout the encryption process. The DES algorithm divides the binary plaintext into blocks of 64 bits each, resulting in a block size of 64 bits.

Before anything else is done, the last block is padded if it is not exactly 64 bits long. Padding ensures that additional data is included in the block to increase its length to 64 bits. Padding can make sure the encrypted data is more difficult to decrypt.

In order to prevent an attacker from predicting the plaintext by simply knowing the algorithm, keys are employed to alter the outcome of an encryption operation.

In DES, a single key is utilized to create subsequent keys that are used during each "round". The DES algorithm is applied 16 times to create the final ciphertext; each application is referred to as a round, with the results serving as the input for the subsequent round. It allows for the greatest amount of plaintext confusion.

Now, we start by selecting a random 64-bit value to serve as our key K. Remember that in order to communicate, the sender and the receiver must both possess the same 64-bit key.

There must be one subkey every round. This subkey is unique to that roundwhich is exclusive to that round and effectively a permutation of our master key K that we established at the beginning. One subkey is created for every round, for a total of 16 subkeys. K1 to K16 are used to identify them.

The key is first permuted using the Permuted Choice-1 (PC-1) table to create our round keys. The following PC1 table will be used to reorder the components of our data block.

The data block's "Left" and "Right" halves are denoted by the letters "C" and "D". The numbers in the table determine which bits of the input key go in the left or right-hand-side parts of the key scheduling state.

C:

D:

TABLE:- PC1

Each bit of the original key is moved around and assigned a new location in line with the table during the PC-1 permutation. The 57th bit from the original key will be entered into the first cell of table "C" since it contains the value 57. The second bit of our new key will be the 49th bit from the previous block because the second cell displays the number 49. The remaining integers from the old block are similarly put in the table "C" order to create our new key. After placing the block in the order of table "C", we go on to table "D" to finish the second half of our new key.

You may have observed that the table and the key are just 56 bits long, as opposed to 64 bits. It is due to the fact that every eighth bit-8, 16, 24, 32, 40, 48, and 56 is designated for use as parity bits in order to confirm that the key has been successfully received. These parity bits give the DES algorithm the practical security of a 56 bit key.

We have now divided our 56 bit key into left and right halves, each of which is 28 bits long. It will be our guide moving forward.

After that, the key is moved left, either one bit or two bits, depending on the round number. The table below provides the precise number to shift:

In these rounds, the numbers are moved to the left by the distances listed in the table, applying each shift to the outcome of the round before it.

For instance, if we're at the fifth encryption round and our key is 1101101101101101, the table says we must left-shift it by two spaces. Because of this, our key after this round will be: 0110110110110111.

As a result, sixteen distinct subkeys are produced, one for each DES round. After that, the key is permuted using the provided Permuted Choice-2 table. Now, we rearrange the bits in our key once more in accordance with the table below.

The key is shuffled similarly to the previous permutation so that the new position of the key bit is determined as shown by the table.

Table: PC2

As a result, the 14th bit of the key is placed in the first position of the new permuted key, the 17th bit is placed in the second position, etc. Further examination reveals that the newly produced key only has 48 bits, as opposed to the previous keys' 56 bits.

Encryption Process in DES Algorithm:

Initial Permutation Function:

The plaintext is divided into blocks of 64 bits, just as we did with the key. The information that needs to be encrypted and sent from sender to receiver is known as the plaintext. If the final block is shorter than the required 64 bits, it is also padded.

The text is then confused by the initial permutation function before any processing is done on it. The Initial Permutation, or IP, has no importance in terms of cryptography.

The binary coded message's bits are ordered according to the Initial Permutation table, and the permutation is carried out similarly to how we did it with the key. This step's output serves as the input for the following one:

Block splitting:

Blocks are divided into two parts, a left block L0 made up of 32 bits and a right block R0 also made up of 32 bits, when the IP procedure is complete.

We move on to the next function after the blocks are separated. During the first round, the right half of the block is taken and put through the following processes:

1. Expansion Permutation (E)
2. Key mixing
3. Substitution (S1, S2,...,S8)
4. Permutation (P)

A) Expansion Permutation (E):

The expansion permutation achieves three objectives, one of which is the avalanche effect, in which the output of two distinct bits is directly influenced by one bit of input data. In order to have the same length as the subkey for the following step, this step also ensures that the right half has 48 bits.

A case study of the avalanche impact

Another significant result of the expansion permutation is the ability to compress the data during the substitution operation by lengthening the output relative to the input.

After that, the blocks are rearranged using the expansion function table below:

With deep examination, we can see that the table contains a few repeating blocks. The block will increase from 32 to 48 bits as a result.

Table:E

B) Key Mixing ():

Following the block's expansion to 48 bits, we apply the subkey of the first round that we obtained from the prior key scheduling. After that, the subkey is used to modify the block using the XOR table.

For instance, if the enlarged key's final eight bits are 01001011, the key following the key mixing step will be: 10110100.

The resultant block is advanced to the following stage.

C) Substitution (S):

Substitution is employed to add complexity to the data, making it harder to understand. Each 6 bit input is converted into a 4 bit output using 8 pre-built tables known as substitution boxes or S-Boxes.

The MSB and LSB are extracted from the 6 bit input and transformed to decimal number X. The row number of the S-box is provided by this number, i.e, X. After that, change the middle four bits of the input into the decimal number Y. We are providing the column number to lookat by Y number. After that, turn the S-Box number that corresponds into a 4 bit binary number. As a result, we were able to successfully transform a 6 bit input into a 4 bit output.

D) Permutation (P)

The F function is once again permuted using the P table of permutations below:

Now, we have completed all of the phases of the F function. The encrypted data we have obtained has a mathematical value known as f(R0, K1). It indicates that the result depends on the first round's subkey and the block R0's initial right side.

Now, we take this value and carry out the subsequent actions:

i) XORing with the Left Block:

Next, using the left half of the block we left earlier and the f(R0,K1) block we obtained from permuting in the previous step, we do an XOR operation. We now have R1, the outcome of the preliminary processing.

ii) 15 more times:

To complete 16 rounds of processing, the aforementioned 3 processes are repeated 15 more times. The processing of the blocks is illustrated in the following diagram: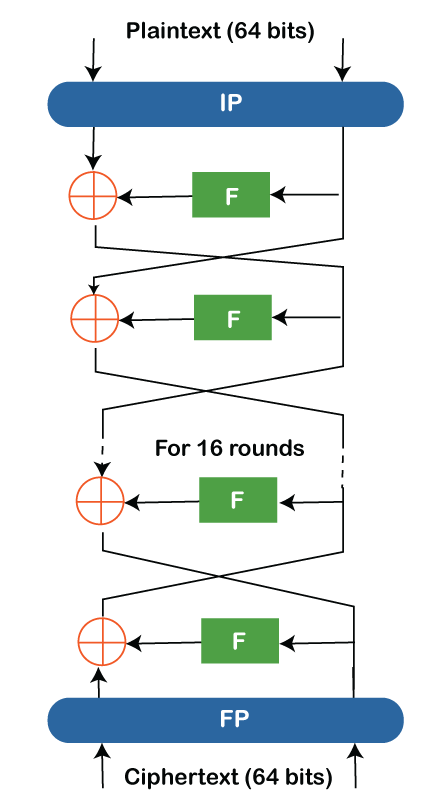

iii) Final Permutation:

Using the provided f(R0, K1) table, the outcome of the last round is permuted one last time. In this case, the table f(R0,K1) is the inverse of the starting table P. The ciphertext generated by the DES algorithm is the final product of this inverse permutation table.

Process of Decryption in the DES Algorithm

Now, we'll go over the DES decryption procedure:

The algorithm has a Feistel structure, which facilitates straightforward decryption. The sole difference between the encryption and decryption processes is that the subkeys are used backwards during decryption.

The data is divided into two parts after going through the first permutation, P. The F function carries over the right half. However, this time the 16th subkey gets registered, and the rest of the process is business as usual. Once the result from the F function is achieved, the left side of the resulting block is XORed. By taking the subkeys in the other direction from the encryption, the procedure is repeated. After the sixteenth round, the plaintext is finally received.

Modes of Operation for DES

Although the DES algorithm encrypts plaintext, its short effective key length makes it susceptible to various brute force attacks. It is especially true in the modern world, where cloud computing and supercomputers offer processing power far beyond that of the computers available in the 1970s, when the DES was designed.

As a result, the DES algorithm was employed for all practical purposes along with various modes of operation based on the applications and uses.

The following are a few of the essential modes of operation:

Electronic Code Book (ECB).

Every block of the input plaintext is directly encrypted with the DES algorithm to produce a block of ciphertext.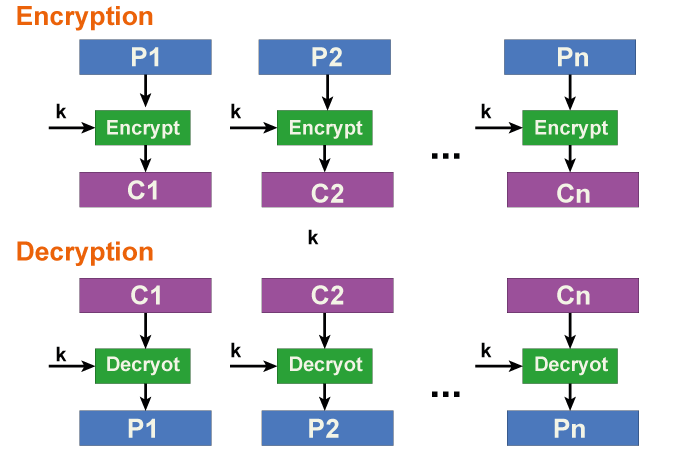

Cipher Block Chaining (CBC):

It is an improvement over ECB in terms of security. After being XORed with the plaintext in this case, the previous cypher block is provided as an input to the following encryption cycle.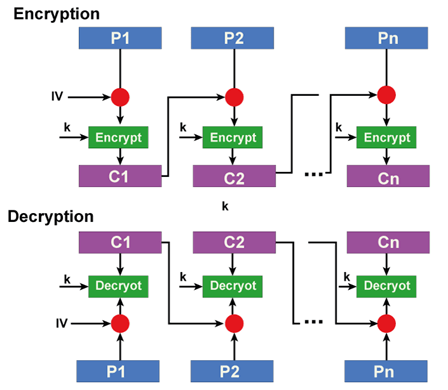

CFB (Cipher Feedback Mode):

In this manner, an Initialization Vector (IV) is a unique variable. It is utilized to start the encryption process. The IV is used in the initial encryption, and the output from earlier encryptions is the input for all subsequent ones.

Each round's output is equally split into s-bits and b-bits on the left and right, respectively. After that, the following round of encryption uses the s-bits to XOR the plaintext.

OFB (Output Feedback Mode):

The sole difference between DES and the Cipher Feedback is that the output is delivered to the following round as feedback rather than the s-bits.

DES Algorithm Implementations and Testing

The DES algorithm is implemented using the following C++ code:

1) Generating a Key:

The technique uses 16 separate subkeys during its 16 rounds of encryption.

Output:

Key 1: 000110010100110011010000011100101101111010001100
Key 2: 010001010110100001011000000110101011110011001110
Key 3: 000001101110110110100100101011001111010110110101
Key 4: 110110100010110100000011001010110110111011100011
Key 5: 011010011010011000101001111111101100100100010011
Key 6: 110000011001010010001110100001110100011101011110
Key 7: 011100001000101011010010110111011011001111000000
Key 8: 001101001111100000100010111100001100011001101101
Key 9: 100001001011101101000100011100111101110011001100
Key 10: 000000100111011001010111000010001011010110111111
Key 11: 011011010101010101100000101011110111110010100101
Key 12: 110000101100000111101001011010100100101111110011
Key 13: 100110011100001100010011100101111100100100011111
Key 14: 001001010001101110001011110001110001011111010000
Key 15: 001100110011000011000101110110011010001101101101
Key 16: 000110000001110001011101011101011100011001101101

2) Plaintext encryption to produce Ciphertext

The plaintext that needs to be encrypted is split into two equal halves and goes through 16 encryption rounds. After that, the ciphertext is produced by combining them.

Output:

Plaintext: 1010101111001101111001101010101111001101000100110010010100110110
Ciphertext: 1001111000100110100111110101101011111010010011011011101101110000