Hamilton Cycle Detection in C++

In this article, we will discuss Hamilton Cycle Detection in C++ with several examples.

What is Hamiltonian Cycle?

Hamiltonian Cycle or Circuit G is a cycle that travels around each vertex exactly once before returning to the first vertex. A graph is referred to as Hamiltonian if it has a Hamiltonian cycle; otherwise, it is non-Hamiltonian.

There is currently no effective solution available to address the well-known NP-complete problem of finding a Hamiltonian Cycle in a graph for all known forms of graphs. It can be solved for small or specialized types of graphs.

The Hamiltonian Cycle problem has real-world applications in a number of disciplines, including computer science, network design, and logistics.

What do you mean by Hamiltonian Path?

In a graph G, a Hamiltonian Path is a path that visits each vertex precisely once and is not required to go back to the starting vertex. Finding a Hamiltonian Path in a general graph is NP-complete and can be difficult, much like the Hamiltonian Cycle issue. Although, it is frequently a simpler job than locating a Hamiltonian Cycle.

Applications for Hamiltonian Paths include circuit design, graph theory research, and determining the best paths in transportation networks.

Backtracking:

Backtracking is an algorithmic method for solving problems based on recursion that involves creating each and every solution incrementally and eliminating any solutions that fail to satisfy the restrictions of the problem at any moment.

Let's review the definition of a Hamiltonian cycle.

Hamiltonian cycle:

In order to return to the starting vertex from any source vertex, we must visit each of the vertices exactly once.

Let's examine the problem now.

Problem Statement:

Let us take an undirected graph with N nodes. This graph is shown as an adjacency matrix with dimensions N x N. It is our task to print every conceivable Hamiltonian cycle.

Example:

This is how the provided graph is shown: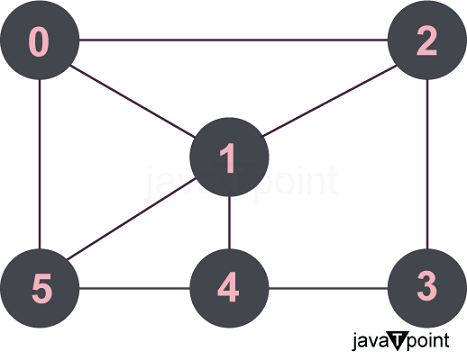

The given graph is represented by an adjacency matrix.

{ 0, 1, 1, 0, 0, 1 }

{ 1, 0, 1, 0, 1, 1 }

{ 1, 1, 0, 1, 0, 0 }

{ 0, 0, 1, 0, 1, 0 }

{ 0, 1, 0, 1, 0, 1 }

{ 1, 1, 0, 0, 1, 0 }

Output:

0 1 2 3 4 5 0

0 1 5 4 3 2 0

0 2 3 4 1 5 0

0 2 3 4 5 1 0

0 5 1 4 3 2 0

0 5 4 3 2 1 0

We can see that by going over every vertex in the graph exactly once, we can get to our source (in this case, 0), by traversing the graph in the form 0->1->2->3->4->5->0. As shown in our report, we may repeat the same process using several pathways.

Working mechanism:

The next step is to take the following method in order to print every Hamiltonian cycle in an undirected graph.

In order to determine whether the vertex being considered at the moment is not already part of the path and is not next to the preceding vertex, we must first build a function.
The vertex can be safely counted if the first two conditions are met.
After that, the function to locate all Hamiltonian cycles will be defined. There will be a path from the last vertex to the first vertex and all of the graph's vertices will be present.
The source vertex will be a part of our path, and the full path will be printed. After printing the path, the source vertex must be removed.
To find a new path for the upcoming vertices, repeat the aforementioned stages.
We will print all conceivable Hamiltonian cycles. We will mention that no hamiltonian cycles are feasible if the aforementioned conditions are not met.

To Print All Hamiltonian Cycles in an Undirected Graph, Use This Pseudocode:

procedure isSafe(int v, int graph[][6], vector<int> path, int pos):

1.  If graph[path[pos - 1]][v] == 0:

        return false

2.  for ( i = 0 to pos) 

        if (path[i] == v): return false;

3.  return true

4. end procedure

procedure FindHamCycle(int graph[][6], int pos, vector<int> path, bool visited[], int N):

1.  if (pos == N):

          if (graph[path[path.size() - 1]][path[0]] != 0):

              path.push_back(0)

              for (i = 0 to path.size()): 

cout << path[I] << " "

    path.pop_back()

hasCycle = true

     return

2.  for ( v = 0 to N):

          if (isSafe(v, graph, path, pos) && !visited[v]):

              path.push_back(v)

              visited[v] = true

    FindHamCycle(graph, pos + 1, path, visited, N)

              visited[v] = false;

     path.pop_back()

3. end procedure

procedure hamCycle(int graph[][6], int N):

 hasCycle = false

 vector<int> path

 path.push_back(0)

 bool visited[N]

 for(i=0 to N):

          visited[i] = false

 visited[0] = true

 FindHamCycle(graph, 1, path, visited, N)

 if (!hasCycle): cout << "No Hamiltonian Cycle" << "possible " << endl
end procedure

Program:

// C++ program to Print all Hamiltonian Cycles in an Undirected Graph
#include <bits/stdc++.h>
using namespace std;

const int V = 6; // Number of vertices in the graph

void printHamiltonianCycle(int path[], int N) {
    cout << "Hamiltonian Cycle: ";
    for (int i = 0; i < N; i++) {
        cout << path[i] << " ";
    }
    cout << path[0] << endl;
}

bool isSafe(int v, int pos, int path[], int graph[V][V], bool visited[]) {
    if (graph[path[pos - 1]][v] == 0) {
        return false;
    }

    if (visited[v]) {
        return false;
    }

    return true;
}

bool findHamiltonianCycleUtil(int graph[V][V], int path[], int pos, bool visited[]) {
    if (pos == V) {
        // Check if there's an edge from the last vertex to the first vertex
        if (graph[path[pos - 1]][path[0]] == 1) {
            printHamiltonianCycle(path, V);
            return true;
        } else {
            return false;
        }
    }

    for (int v = 1; v < V; v++) {
        if (isSafe(v, pos, path, graph, visited)) {
            path[pos] = v;
            visited[v] = true;

            if (findHamiltonianCycleUtil(graph, path, pos + 1, visited)) {
                return true;
            }

            path[pos] = -1; // Backtrack
            visited[v] = false;
        }
    }

    return false;
}

bool findHamiltonianCycle(int graph[V][V]) {
    int path[V];
    bool visited[V];

    for (int i = 0; i < V; i++) {
        path[i] = -1;
        visited[i] = false;
    }

    // Starting from vertex 0
    path[0] = 0;
    visited[0] = true;

    if (!findHamiltonianCycleUtil(graph, path, 1, visited)) {
        cout << "No Hamiltonian Cycle possible" << endl;
        return false;
    }

    return true;
}

int main() {
    int graph[V][V] = {
        {0, 1, 1, 0, 0, 1},
        {1, 0, 1, 0, 1, 1},
        {1, 1, 0, 1, 0, 0},
        {0, 0, 1, 0, 1, 0},
        {0, 1, 0, 1, 0, 1},
        {1, 1, 0, 0, 1, 0},
    };

    findHamiltonianCycle(graph);

    return 0;
}

Output: