Merge Sort Pseudocode C++:Merge Sort is a popular sorting algorithm that effectively sorts a list or array of elements using the "divide and conquer" principle. Here's an overview of how Merge Sort functions: Divide: If the number of elements is odd, the unsorted list is divided into two equal (or about equal) halves. Recursively, this procedure goes on until each sub-list only has one entry, which is automatically sorted. Conquer: The method begins by sorting these sub-lists before combining them. To produce new sorted sub-lists, it starts with pairs of sub-lists and repeatedly merges them. This procedure is repeated until just one sorted list, which is the sorted counterpart of the initial unsorted list, is left. Merge: Comparing entries from the two sub-lists, and the merging procedure chooses the smaller (or bigger) element to add to the new merged list. The comparison and merging process is repeated until the combined list contains every entry from both sub-lists. The main benefit of Merge Sort is that it is a reliable, effective, and predictable sorting algorithm with an average and worst-case time complexity of O(n log n). Its divide-and-conquer strategy makes sorting huge datasets or linked lists extremely advantageous. However, during the merging operation, it needs more RAM for the temporary sub-lists. Types of Implementations of Merge Sort:Recursive top-down merge sort: The most typical Merge Sort implementation is this kind. The array is split into smaller sub-arrays until each sub-array only has one element, at which point it merges the sub-arrays back together in a sorted way. This strategy is simple to comprehend and put into practice. However, because of recursion, it could result in more function calls. Iterative Bottom-Up Merge Sort: In this case, the method begins by considering each element as a distinct sub-array that has been sorted. After that, until the entire array is sorted, it continually combines nearby sub-arrays. In comparison to the recursive method, Bottom-Up Merge Sort is frequently more memory-efficient and may have reduced function call overhead. In-Place Merge Sort: Traditional Merge Sort needs additional RAM to hold temporary sub-arrays when merging. By reordering components inside of the original array without utilizing additional memory, In-Place Merge Sort seeks to reduce memory utilization. Due to additional element motions, implementation is often more difficult and may result in lower performance. Parallel merge sort: Parallel Merge Sort breaks the sorting operation into smaller sub-tasks and sorts them concurrently utilizing multiple processor cores, taking advantage of the emergence of multi-core CPUs. Large dataset sorting can be considerably sped up with this method, although parallel computing infrastructure is needed. Hybrid merge sort: Merge Sort is combined with another sorting algorithm, such as Insertion Sort or Quick Sort, in hybrid merge sort. Based on the size of the sub-arrays, the sorting method is chosen dynamically. To cut down on overhead, it changes to a quicker but less effective sorting algorithm for tiny sub-arrays. Natural Merge Sort: Designed for data having natural runs (sequences of ordered items) or data that is only partially ordered. It recognizes these runs, effectively combines them while preserving their sequence, and minimizes extra effort. External Merge Sort: Used to sort big datasets that don't fit completely in memory. Combines the sorted data pieces on a disc after dividing the data into chunks and sorting them in memory. Frequently applied to database systems and sorting for external storage. Merge Sort for Linked Lists: This implementation is made to sort linked lists efficiently rather than using arrays. It divides linked lists into smaller lists before merging them all at once in a recursive fashion. Applications of Merge Sort:General-Purpose Sorting: Merge Sort is a popular technique for quickly sorting huge datasets. It is a well-liked option for generic sorting jobs because of its O(n log n) time complexity, which guarantees high performance on both small and big datasets. External Sorting: Merge Sort works well for organizing large datasets that don't fit totally in memory. Data is separated into smaller bits, sorted in memory, and then combined on disc through external sorting algorithms. For programs like database management systems, this is crucial. File and Data Management: Merge To maintain directory hierarchies and sort file listings, sort is used in file systems. It facilitates speedy and effective file retrieval procedures. Inversion Counting: Merge Sort is used to count the number of inversions (out-of-order pairs) in an array. This is valuable in various applications, such as analyzing the similarity between documents and detecting data anomalies. Parallel Processing: Parallel Merge Sort leverages multiple processor cores to sort data concurrently. This is especially useful in high-performance computing and distributed systems to accelerate sorting tasks. Merge Join in Databases: In database systems, Merge Sort is utilized in the merge join operation, which is essential for joining large datasets efficiently. This speeds up database queries involving multiple tables. Merge Sort for Linked Lists: Merge Sort is the preferred sorting algorithm for linked lists due to its stability and efficient merging of sorted lists. It's widely used in languages like Java for sorting linked data structures. Visualization and Graphics: In computer graphics and visualization, Merge Sort can be used to determine the visibility of objects in a 3D scene. It helps in rendering objects from back to front to create realistic visuals. Geographical Information Systems (GIS): GIS applications often require sorting geographic data, such as points or polygons. Merge Sort is used to organize and query spatial data efficiently. Natural Language Processing (NLP): Merge sort can be applied in NLP tasks, like text summarization and document clustering, where sorting is essential for organizing and analyzing textual data. Optical Character Recognition (OCR): OCR systems use Merge Sort for sorting recognized characters and symbols to reconstruct text from scanned documents. Scientific Computing: Merge Sort is used in various scientific applications for sorting and processing large datasets, such as analyzing experimental results or simulations. Pseudocode Implementation of Merge sort:Output: 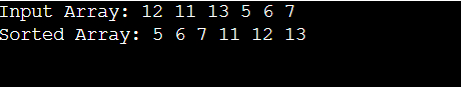
Explanation: The C++ code that is provided in the above article uses the popular and efficient merge sort algorithm. This method divides an unsorted array into smaller and sorted sub-arrays that are combined to produce a completely sorted array. Let's split down the functionality of the code into sentences: The mergeSort function, which accepts an unsorted array as input, is defined in the code. The core of the Merge Sort algorithm is this function. The array is considered sorted and returned in its present state if it has one or no entries, starting with a base case check. In any other situation, the array is divided in half. Divide and conquer: The mergeSort function divides the input array into the left and right smaller arrays. The middle index of the input array is used to divide the array. The mergeSort method is then recursively fed to both the left and right arrays. This recursive division successfully breaks the problem into smaller pieces that are easier to handle and iterates until each sub-array has only one element. Merge Function: This function in the code is used to create a single sorted array known as a result by merging two sorted arrays known as array1 and array2 together. It chooses the smaller in-size item and adds it to the result when comparing each entry in the two arrays. Until all entries from both arrays are present in the final result, the process is repeated. A key component of Merge Sort, this merging procedure makes sure that two sorted halves are joined into a bigger sorted whole. Main Function: An example array (inputArray) is constructed and presented as the input in the main function. Then, this array is subjected to the merge sort algorithm, resulting in a sorted array (sortedArray). To illustrate the sorting procedure, both the input and the sorted arrays are shown. How merge sort is different from other sorting algorithms:Divide and Conquer Approach: Merge Sort utilizes a divide-and-conquer method. In order to get the final sorted result, it divides the sorting function into smaller subproblems, sorts each one separately, and then combines the sorted subproblems. This recursive method makes sure that Merge Sort consistently has a worst-case time complexity of O(n log n). Natural Stability: Merge Sort is naturally stable when sorting data. Throughout the sorting process, it maintains the relative order of comparable components. Other algorithms, such as Quick Sort, are only sometimes stable and may need extra modifications to be stable. Performance Predictability: Merge Sort promises to have a worst-case time complexity of O(n log n), which is more predictable than certain other algorithms like Quick Sort, which can have worst-case time complexities of O(n2). In real-time systems with critical applications, this predictability is essential. Parallel processing: Merge Sort easily adapts itself to multi-threaded operations. By breaking the data up into smaller pieces, sorting each one separately, and then joining the sorted segments, parallelization is very simple. Merge Sort is now effective in remote computing environments and on multi-core systems. Greater Memory Usage: Merge Sort has the downside of using more memory during the merging process. According to the amount of the supplied data, it often requires more space. As a result of sorting components in place, algorithms like Quick Sort and Heap Sort frequently consume less RAM. Flexibility: Merge sort may be customized to work with a variety of data structures, such as arrays and linked lists. It requires little change and provides constant performance across many data structures. In contrast, some alternative algorithms could be less flexible overall but better suited to certain data formats. Swaps vs. Comparisons: Merge Sort depends mostly on element comparisons for sorting, making it appropriate in situations where comparisons are affordable but element swaps are expensive. In certain circumstances, other sorting algorithms, including Insertion Sort and Bubble Sort, which concentrate on minimizing element swaps, could perform better. Drawbacks of Merge Sort:Extra Memory Consumption: The amount of memory needed for sorting depends on the size of the incoming data. Particularly, during the merging process, it requires room for temporary arrays. This makes it less appropriate for sorting big files or in memory-constrained contexts when working with huge datasets that might not fit into memory. Slower for Small Lists: Splitting and merging subarrays adds overhead to Merge Sort's divide-and-conquer strategy. As a result, it might not be as effective as alternative algorithms for sorting restricted lists or arrays with few entries, such as Insertion Sort or Bubble Sort. The overhead of function calls and recursion can influence performance for small datasets. In practice, Quick Sort Outperforms Merge Sort: While Merge Sort guarantees a consistent worst-case time complexity of O(n log n), Quick Sort frequently outperforms it in practice. The average-case performance of Quick Sort frequently exceeds that of Merge Sort. Additionally, Quick Sort has the benefit of sorting locally, which lowers memory use. Complex Implementation: When compared to other straightforward sorting algorithms like Bubble Sort or Selection Sort, Merge Sort implementation might be more challenging. Careful coding is needed to properly manage the recursive calls and merge stages, which might increase the chance of mistakes. Conclusion:In conclusion, the given Merge Sort pseudocode in C++ represents the Merge Sort algorithm in an understandable and organized manner. It demonstrates Merge Sort's signature recursive divide-and-conquer strategy. This pseudocode describes the steps involved in dividing an array into smaller subarrays, sorting each one separately, then merging the sorted subarrays back together to create a completely sorted array. This pseudocode demonstrates a sophisticated sorting algorithm called merge sort, which is known for its consistency and predictable time complexity. It is useful in many computer science applications and programming activities because of its efficiency in handling huge datasets and capacity for steady sorting.
Next TopicObjective C vs C++
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










