Maximum Number of Edges to be Added to a Tree so that it stays a Bipartite Graph

The goal is to convert an N-node tree into a bipartite graph by adding as many edges as possible.

Remember that self-loops and multiple edges are not permitted, although cycles are.

Illustration: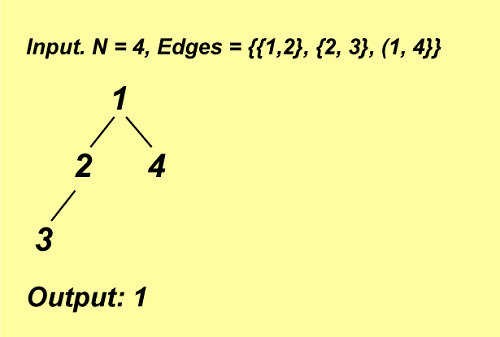

Maximum Number of Edges to be Added to a Tree so that it stays a Bipartite Graph

Explanation: An edge connecting nodes 3 and 4 can be added to keep the graph bipartite.

There can only be one edge added to the graph to make it bipartite.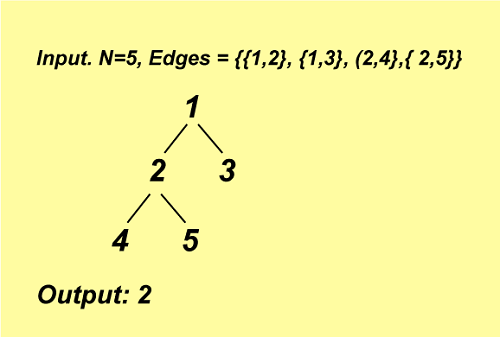

Explanation: Even if two edges are added, (3, 4) and (3, 5), the graph remains bipartite.

Simple Approach:

The basic solution to the problem is as follows:

Each node in the tree should be given a colour, resulting in a connection between a black and a white node (A tree is always bipartite, hence there is always such a configuration).

Then, for each feasible pair of nodes, determine whether an edge may be added between them.

To put the above idea into action, follow the procedures outlined below:

Initially, traverse the tree, assigning each node a black or white colour so that each edge connects a black and a white node. (All trees are bipartite.)
Check to determine if an edge can be added between each node pair by iterating over them all.
If the nodes are different colours and there isn't an edge between them, an edge can be added. So, increase the number.
There is no other way to give anything an edge.
The answer is the total value of the count.

The aforementioned approach is implemented in the following manner.

C++ Program:

#include <bits/stdc++.h>
using namespace std;

void dfs(int node1, int pr, bool isitBlack,
		vector<vector<bool> >& adjc,
		vector<bool>& colour)
{

	colour[node1] = isitBlack;

	for (int i = 1; i < adjc.size(); ++i) {

		if (!adjc[node1][i] || i == pr)
			continue;

		dfs(i, node1, !isitBlack, adjc, colour);
	}
}

long long maximumEdges(int num,
				vector<pair<int, int> > edges)
{
	vector<vector<bool> > adjc(num + 1,
							vector<bool>(
								num + 1, 0));
	for (auto i : edges) {
		adjc[i.first][i.second] = 1;
		adjc[i.second][i.first] = 1;
	}
	vector<bool> colour(num + 1);
	dfs(1, 0, 1, adjc, colour);

	long long answer = 0;

	for (int i = 1; i <= num; ++i) {
		for (int j = i + 1; j <= num; ++j) {

			if (colour[i] != colour[j]
				&& !adjc[i][j])
				answer++;
		}
	}

	return answer;
}

int main()
{
	int Num = 4;
	vector<pair<int, int> > edges
		= { { 1, 2 }, { 2, 3 }, { 1, 4 } };
	cout << maximumEdges(Num, edges);
	return 0;
}

Output:

Time Complication will be O(N²).
Auxiliary space will be O(N²).

Efficient Approach

The time required in the preceding approach can be reduced by making the following observation:

Assume the tree has B black nodes and W white nodes at first. As a result, a bipartite graph constructed from these nodes can have the greatest number of B*W edges.
As a result, with N nodes, the maximum number of edges that can be added to the tree is B*W - (N-1) [as a tree with N node has N-1 edges].

Follow the instructions below:

Initially, traverse the tree, assigning each node a black or white colour so that each edge connects a black and a white node. (All trees are bipartite.)
Determine the number of black and white nodes.
Determine the maximum number of edges that can be added using the formula derived above from the observation.

The aforementioned approach is implemented in the following manner.

C++ Program:

#include <bits/stdc++.h>
using namespace std;

int dfs(int node1, int par, bool isitBlack,
		vector<vector<int> >& adj)
{
	int nos_Of_Black = isitBlack;
	for (int i : adj[node1]) {
		if (i == par)
			continue;

		nos_Of_Black
			+= dfs(i, node1, !isitBlack, adj);
	}
	return nos_Of_Black;
}
long long maximumEdges(int num,
				vector<pair<int, int> > edges)
{
	vector<vector<int> > adj(num + 1);
	for (auto i : edges) {
		adj[i.first].push_back(i.second);
		adj[i.second].push_back(i.first);
	}
	int nos_Of_Black = dfs(1, 0, 1, adj);

	int nos_Of_White = num - nos_Of_Black;
	return (1LL * (nos_Of_Black)
				* (nos_Of_White)
			- (num - 1));
}
int main()
{
	int Num = 4;
	vector<pair<int, int> > edges
		= { { 1, 2 }, { 2, 3 }, { 1, 4 } };
	cout << maximumEdges(Num, edges);
	return 0;
}

Output: