Maximum size square sub-matrix with all 1s in C++

In this article, you will learn how to find a maximum size square sub-matrix with all 1s in C++.

Problem statement:

You are given a 2D matrix, and you have to search for a maximum-sized matrix that contains all elements as one.

Input format:

A 2D matrix of order n X m.

Output format:

An integer of the area of the maximum-sized matrix.

It means the sum of all the ones in the maximum-sized matrix.

Explanation for an example is as follows:

Matrix is:

{{'1', '0', '1', '0', '0'},

{'1', '0', '1', '1', '1'},

{'1', '1', '1', '1', '1'},

{'1', '0', '0', '1', '0'}}

Output:

Maximum sized matrix is:

{{'1', '1'},

{'1', '1'}}

Method 1: Brute Force method

Let's take an example to find the Maximum size square sub-matrix with all 1s using the brute force method in C++.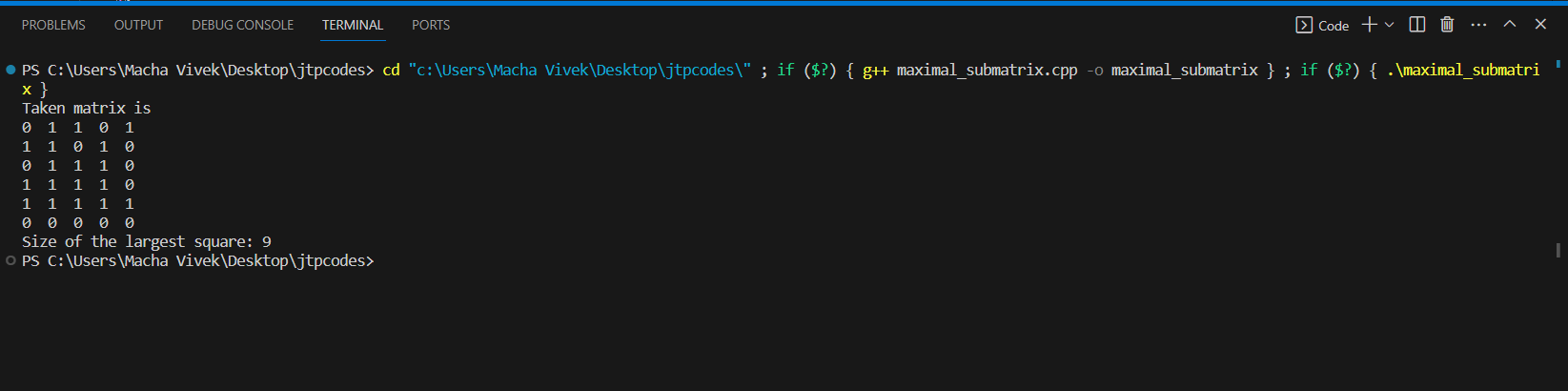

#include <iostream>
#include <vector>
using namespace std;
int maximalSquare(vector<vector<char>>& matrix) {
 if (matrix.empty()) return 0;
 
 int rows = matrix.size();
 int cols = matrix[0].size();
 int maxSize = 0;
 
 for (int i = 0; i < rows; ++i) {
 for (int j = 0; j < cols; ++j) {
 if (matrix[i][j] == '1') {
 int size = 1;
 bool isSquare = true;
 while (i + size < rows && j + size < cols && isSquare) {
 for (int k = i; k <= i + size; ++k) {
 if (matrix[k][j + size] == '0') {
 isSquare = false;
 break;
 }
 }
 for (int k = j; k <= j + size; ++k) {
 if (matrix[i + size][k] == '0') {
 isSquare = false;
 break;
 }
 }
 if (isSquare) size++;
 }
 maxSize = max(maxSize, size);
 }
 }
 }
 
 return maxSize * maxSize;
}
int main() {
 vector<vector<char>> matrix = {
 { '0', '1', '1', '0', '1' },
 { '1', '1', '0', '1', '0' },
 { '0', '1', '1', '1', '0' },
 { '1', '1', '1', '1', '0'},
 { '1', '1', '1', '1', '1' },
 { '0', '0', '0', '0', '0' } 
 };
 cout <<"Taken matrix is "<< endl;
 for(int i=0;i<matrix.size();i++){
 for(int j=0;j<matrix[0].size();j++){
 cout << matrix[i][j] <<" ";
 }
 cout << endl;
 }
 int result = maximalSquare(matrix);
 cout << "Size of the largest square: " << result << endl;
 
 return 0;
}

Output:

Maximum size square sub-matrix with all 1s in C++

Explanation:

The above program is used to find the submatrix, which is of size n or matrix of order n X n. It is the brute force method, where the main idea or thought process is iterating through the matrix. First, take the submatrix of fixed size 2 and slide that sub-matrix to the right until it meets the end of the matrix. If they meet the end of the matrix horizontally, make that submatrix move down by one-step and from the starting and then again slide to the end of the matrix. It makes a fixed-sized matrix of 2 X 2 order.

After that, change the order of the submatrix; change it to 3 X 3. Again, do the same process for all the sub-matrices with different sizes. It will end when no more sub-matrices are made. Here, you have to do one thing while iterating or sliding through the matrix: checking whether all the elements that are present in the matrix are all one. If all elements are one, store the size of the matrix in one variable. Every time you get a sub-matrix with a size greater than the variable, you update the variable's value with a new size where each sized matrix will contain only one. After all this process, print the variable you stored. It will give you the desired output. This method could be more optimal. It takes more time and space to get the result.

Method 2: Using Dp Array

Let's take an example to find the Maximum size square sub-matrix with all 1s using the Dp array in C++.

#include <iostream>
#include <vector>
using namespace std;
int findMaxSquare(vector<vector<char>>& matrix, vector<vector<int>>& dp, int i, int j) {
 if (i < 0 || j < 0 || matrix[i][j] == '0') return 0;
 if (dp[i][j] != -1) return dp[i][j];
 
 int left = findMaxSquare(matrix, dp, i, j - 1);
 int up = findMaxSquare(matrix, dp, i - 1, j);
 int diagonal = findMaxSquare(matrix, dp, i - 1, j - 1);
 
 dp[i][j] = 1 + min(min(left, up), diagonal);
 return dp[i][j];
}

int maximalSquare(vector<vector<char>>& matrix) {
 if (matrix.empty()) return 0;
 
 int rows = matrix.size();
 int cols = matrix[0].size();
 int maxSize = 0;
 
 vector<vector<int>> dp(rows, vector<int>(cols, -1));
 
 for (int i = 0; i < rows; ++i) {
 for (int j = 0; j < cols; ++j) {
 if (matrix[i][j] == '1') {
 maxSize = max(maxSize, findMaxSquare(matrix, dp, i, j));
 }
 }
 }
 
 return maxSize * maxSize;
}
int main() {
 vector<vector<char>> matrix = {
 {'1', '0', '1', '0', '0'},
 {'1', '0', '1', '1', '1'},
 {'1', '1', '1', '1', '1'},
 {'1', '0', '0', '1', '0'}
 };
 int result = maximalSquare(matrix);
 cout << "Size of the largest square: " << result << endl;
 return 0;
}

Output:

Explanation:

To understand the above program, we will first see the variables present in the program. First is the matrix, the input 2D array containing only ones and zeros. Dp array is a dynamic array that stores the computed sub-problem solution to avoid errors in calculation. It helps in optimizing the recursion problem of the program. Initially, all the values in the dp array are set to -1s, showing that it is not computed. Integer i and j are variables that represent the current row and current indices of the matrix. Integers are left, right, and diagonal variables that store the results of recursive calls in the findMaxSquare function. maxSize will keep track of our main output, which is the maximum size of the sub-square.

The base case of the function findMaxSquare is if i or j bounds out of the matrix, it will return zero. After that, we have to do memorization in this function. If i and j in the matrix is calculated and stored in the dp table. It returns the stored result. Otherwise, it recursively calculates the effects of left, upper, and diagonal cells and stores the minimum of the results plus 1 in the dp array. After that, this function will return the size of the largest square at the end.

Method 3: Tabulation method

Let's take an example to find the Maximum size square sub-matrix with all 1s using the tabulation method in C++.

#includ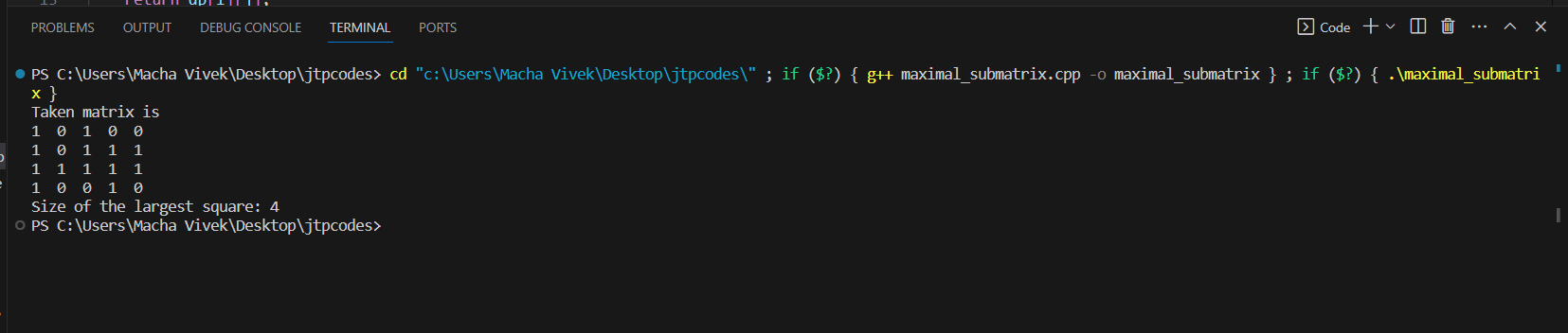e <iostream>
#include <vector>
using namespace std;

int maximalSquare(vector<vector<char>>& matrix) {
 if (matrix.empty()) return 0;
 
 int rows = matrix.size();
 int cols = matrix[0].size();
 int maxSize = 0;
 
 vector<vector<int>> dp(rows + 1, vector<int>(cols + 1, 0));
 
 for (int i = 1; i <= rows; ++i) {
 for (int j = 1; j <= cols; ++j) {
 if (matrix[i - 1][j - 1] == '1') {
 dp[i][j] = 1 + min(min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]);
 maxSize = max(maxSize, dp[i][j]);
 }
 }
 }
 return maxSize * maxSize;
}

int main() {
 vector<vector<char>> matrix = {
 {'1','0','1','0','0'},
 {'1','0','1','1','1'},
 {'1','1','1','1','1'},
 {'1','0','0','1','0'}
 };
 int result = maximalSquare(matrix);
 for(int i=0;i<matrix.size();i++){
 for(int j=0;j<matrix[0].size();j++){
 cout << matrix[i][j] << " ";
 }
 cout<< endl;
 }
 cout << "Size of the largest square: " << result << endl;
 return 0;
}

Output:

Explanation:

The variable present in the program is a matrix, which is the input 2D array containing only ones and zeros. Dp is a dynamic array that stores the computed sub-problem solution to avoid errors in calculation. It helps in optimizing the recursion problem of the program. Initially, all the values in the dp array are set to 0s, showing that it is not computed. Integer i and j are variables that represent the current row and current indices of the matrix. Integers left, right, and diagonal variables store the results.

The program checks each cell in the input matrix. If a cell contains '1', it calculates the size of the largest square that can end at that cell, considering nearby cells on the left, upper, and upper-left diagonal. It keeps track of the biggest square found. Finally, the function returns the area of this largest square made of '1's in the input matrix.

Conclusion:

The perfect conclusion for the above article is as follows:

Brute force:

Time complexity: O((mn)^3)
Space complexity: O(1)

Using dp array:

Time complexity: O(mn^2)
Space complexity: O(mn)

Tabulation:

Time complexity: O(mn)
Space complexity: O(mn)

The brute force approach meticulously examines every possible submatrix, leading to a substantial increase in time complexity. On the other hand, dynamic programming techniques (both top-down and bottom-up) optimize the solution by memorizing intermediate results, significantly decreasing the time complexity. Among these dynamic programming strategies, the bottom-up or tabulation method stands out for its superior efficiency in time and space. Consequently, it is the favoured approach for solving this problem. In summary, although all methods can solve the problem, employing dynamic programming with tabulation offers the most efficient solution, effectively managing time and space complexity.

Next Topicmultimap get_allocator() function in C++

← prev next →