C++ Program to Represent Linear Equations in Matrix Form

Linear Equation is a basic concept in mathematics and science. Linear equations are important in many disciplines, such as computer science, economics, physics, and engineering. It is necessary to express systems of linear equations in matrix form to solve them quickly.

What is a System of Linear Equations?

A group of several linear equations containing one or more variables is called a system of linear equations.

Every linear equation has the following possible forms:

Whereas,

The coefficients of the variables x₁, x₂, x₃,..., xₙ are a₁, a₂, a₃,..., aₙ, and the constant on the right side of the equation is b.

Many of these equations make up a system of linear equations. An illustration of a system of three linear equations in three variables might be as follows:

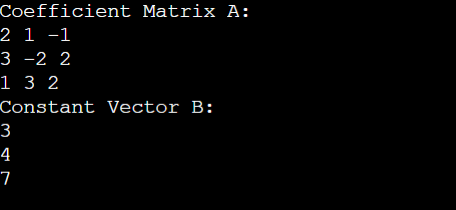
2x + y - z = 3
3x - 2y + 2z = 4
x + 3y + 2z = 7

We will construct a constant vector and a coefficient matrix to express this system as a matrix.

Linear Equation Representation in Matrix Form:-

We can express a system of linear equations compactly and practically using matrix representation. The above-mentioned system of linear equations is expressed as follows:
AX = B
The coefficients of the variables are contained in matrix A, which is the coefficient matrix.
X denotes the variable column vector.
The letter B denotes the column vector of constants on the right side of each equation.

Algorithm to Represent Linear Equations in Matrix Form:-

The following describes the algorithm used to represent linear equations in matrix form:

Make a structure to hold each linear equation's coefficients and constants.
Create a function that takes a vector of linear equations and returns the constant vector B and the coefficient matrix A.
Find how many variables and equations the system contains.
Set up the void matrices A and B.
Add the coefficients of each linear equation to A and the constants to B as we go through the equations.
Show the constant vector B and the coefficient matrix A.

Program:

Let's take a C++ program to illustrate the linear equation in Matrix form:

#include <iostream>
#include <vector>
using namespace std;
// Define a structure for representing linear equations
struct LinearEquation {
 vector<double> coefficients;
 double constant;
};
// Function to represent linear equations in matrix form
void equationsToMatrix(vector<LinearEquation> equations, vector<vector<double>>& A, vector<double>& B) {
 int numEquations = equations.size();
 int numVariables = equations[0].coefficients.size();
 A.clear();
 B.clear();
 for (int i = 0; i < numEquations; i++) {
 A.push_back(equations[i].coefficients);
 B.push_back(equations[i].constant);
 }
}
int main() {
 // Create a system of linear equations
 vector<LinearEquation> equations = {
 {{2, 1, -1}, 3},
 {{3, -2, 2}, 4},
 {{1, 3, 2}, 7}
 };
 // Initialize matrices A and B
 vector<vector<double>> A;
 vector<double> B;
 // Represent the linear equations in matrix form
 equationsToMatrix(equations, A, B);
 // Display the coefficient matrix A
 cout << "Coefficient Matrix A:" << endl;
 for (int i = 0; i < A.size(); i++) {
 for (int j = 0; j < A[i].size(); j++) {
 cout << A[i][j] << " ";
 }
 cout << endl;
 }
 // Display the constant vector B
 cout << "Constant Vector B:" << endl;
 for (int i = 0; i < B.size(); i++) {
 cout << B[i] << endl;
 }
 return 0;
}

Output:

C++ Program to Represent Linear Equations in Matrix Form

Explanation:

1. Describe a Linear Equation Structure:

Every linear equation is represented by a struct called LinearEquation. It is made up of two parts:
- coefficients: A vector that holds the equation's variable coefficients.
- constant: The constant term on the right side of the equation is represented by a double number.

2. Function for Converting Matrices from Linear Equations:

Equations, two empty containers, A (a 2D vector for the coefficient matrix) and B (a vector for the constant terms), and a vector of LinearEquation objects are all required by the function equationsToMatrix.
By looking at the first equation, the function determines the number of variables (numVariables) and the number of equations (numEquations).
After that, any existing data is cleared out of them to make sure the matrices A and vector B begin empty.
It adds the coefficients of each equation iteratively via the equations vector as a row to the A matrix and adds the equation's constant term to the B

3. Main Function:

The program's entry point serves as the primary function.
It builds a system of linear equations by initializing a vector of LinearEquation objects, equations, with their coefficients and constants.

4. Intialize Matrices A and B to start:

The coefficient matrix and the constant vector are defined to be stored in two empty containers, A and B.

5. Call equationsToMatrix Function:

The equations vector, empty matrixes A and B, and the equations vector are passed as inputs to the equationsToMatrix
After processing the linear equations, this function fills in the constant vector B and the coefficient matrix A.

6. Display the Coefficient Matrix A:

The coefficient matrix A is printed by the program to the standard output.
The 2D A vector is traversed using nested loops, and the coefficients are shown row by row.

7. Display the Constant Vector B: