Neural network in C++

In this article, we will discuss the neural network in C++ with its example.

What is a Neural Network?

The neural network is a computational model that has a structure the same as the neuron that is present in the brain. Its functionality is also the same as the neuron. It is like an artificial nervous system for receiving the input information, processing or manipulating it and transmitting it.

Layers of Neural Network

A neural network contains three types of layers: that are input layer, the hidden layer, and the output layer.

Input layer:

There is only one input layer in a model that takes all the inputs from the dataset these inputs are the features. This input information is given to the hidden layers in the Neural network.

Hidden layer:

There will be many hidden layers present in the network. The inputs given by the input layer are modified and converged to get the desired outputs. Suppose there are three hidden layers, the inputs are given to the first hidden layer, and then after updating the weights, these weights are given to the second layer. Then again, the updated weights are given to the third hidden layer. After that, this updated information is given to the output layer.

Output layer:

After processing, the data is made available at the output layer.

Basics of the Neural Networks:

Neurons and layers: Every neuron acts as a biological neuron. Layers are input, hidden, and output layers.

Activation functions: These mathematical functions give the non-linearity or curves to the model. Some of the activation functions are sigmoid, ReLu, etc. These functions make the model learn complex patterns in the data. ReLU and its variants (Leaky ReLU, ELU) are popular choices for hidden layers due to their simplicity and effectiveness in many scenarios. Sigmoid and softmax are commonly used in the output layer, depending on the nature of the problem.

Feedforward and backpropagation: In forward propagation, the weights are updated and converged to predict the accurate output, but in backpropagation, the weights are again decreased and updated to minimize the error.

Loss functions: Loss functions, also known as cost functions or objective functions, quantify the difference between predicted values and actual values. Some loss functions are Mean Squared Error, Binary Cross-Entropy Loss, Categorical Cross-Entropy Loss, Hinge Loss, etc. Choosing an appropriate loss function is important because it directly influences the learning behaviour of the model and ensures the model is optimized effectively for the specific task at hand.

Optimizers: These are used to optimize the weights. Some of them are gradient, Adagrad, adam, stochastic gradient descent, RMSprop optimizers, etc. These are very important to attain convergence and accurate output. Adam is the best optimizer at present.

Weight initialization: Proper initialization of weights is crucial to prevent the vanishing gradient and exploding gradient. Some of them are Xavier or Glorot initialization.

Regularization techniques: These are useful for preventing overfitting and underfitting problems. There are two types of regularization that are L1 regularization that are Lasso regularization, and L2 regularization, which is Ridge regularization. Some of the regularization techniques are the implementation of callbacks and early stopping. Data augmentation is used to avoid underfitting.

Validation and Testing:

Training datasets: The part of the dataset that is useful to train the network to learn from the dataset.

Validation dataset: The validation dataset is a separate portion of the data that is not used for training the model. Instead, it's used to evaluate the model's performance during training.

Test dataset: The test dataset is a completely unseen portion of the data that is used to evaluate the final model after it has been trained and tuned using the training and validation datasets.

Example:

Let's take an example to illustrate the neural network in C++.

Output: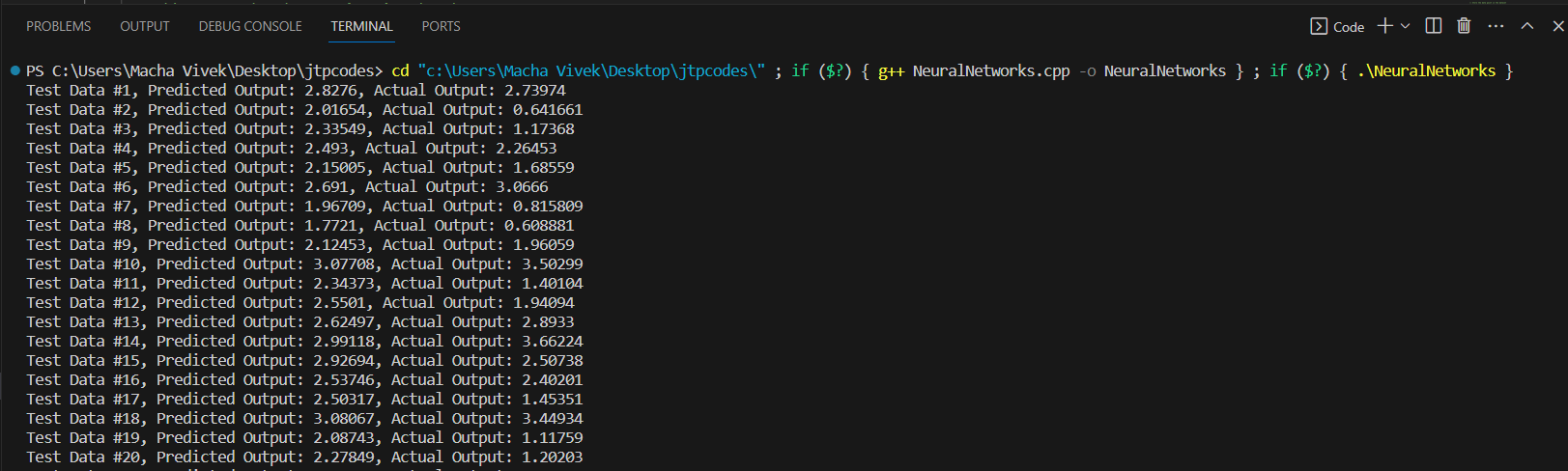

Explanation:

This program is large as it contains all the techniques that are useful for neural networks. So simply divide the code into functions to get a good understanding

Layout of the program:

NeuralNetwork Class:

Constructor:

NeuralNetwork::NeuralNetwork(int inputSize, int hiddenSize, int outputSize)

Activation Function:

double NeuralNetwork::sigmoid(double x)

Activation Function Derivative:

double NeuralNetwork::sigmoidDerivative(double x)

Training Method:

void NeuralNetwork::train(vector<vector<double>>& inputs, vector<double>& targets, int epochs, double learningRate)

Prediction Method:

double NeuralNetwork::predict(vector<double>& input)

Helper Function:

Mean Squared Error Calculation:

double calculateMeanSquaredError(vector<double>& predictedOutputs, vector<double>& actualOutputs)

Main Function:

int main()

NeuralNetwork Constructor:

It initializes the NeuralNetwork object with specific input, hidden, and output layer sizes. It takes three parameters that are inputSize, hiddenSize, and outputSize. This constructor sets up the basic structure of the neural network, preparing it for training and prediction tasks.

Sigmoid function:

It is the activation function that computes the sigmoid activation for a given input value x. The sigmoid function maps any real-valued number to the range between 0 and 1. It is defined as:

Sigmoid(x) = 1 / (1+ e^(-x))

double x - The input value for which the sigmoid activation needs to be calculated.

double - The result of applying the sigmoid function to the input.

The main purpose of this function is to introduce the non-linearity to the network.

This function is called or utilized during both forward propagation and backpropagation.

sigmoidDerivative function:

The sigmoidDerivative function computes the derivative of the sigmoid activation function with respect to its input. The derivative of the sigmoid function σ(x) is given by the formula:

Input is double x whose sigmoid derivate is needed and output is the result of applying the derivative of the sigmoid function to the input.

train function:

Function parameters are:

Inputs: A 2D vector representing the input data for training.

Targets: A vector containing the corresponding target values.

Epochs: It specifies the number of iterations of the training process to run.

learning Rate: It represents the step size at which the weights are updated during each iteration.

The return type of the function are:

Its return type is void. It does not return anything to other functions, but it modifies the internal state of the neural network object.

Variables used in the function:

int epoch: Loop variable representing the current epoch during training.

size_t i: Loop variable representing the index of the current training data point.

size_t j: Loop variable used for iterating through hidden layers.

size_t k: Loop variable used for iterating through input features.

double weightedSum: Temporary variable holding the weighted sum of inputs for a neuron.

double outputError: Represents the error between the predicted output and the actual target value.

vector<double> hiddenOutput: Vector holding the output values from the hidden layer neurons for a given input.

vector<double> hiddenErrors: Vector storing the errors in the hidden layer, used during backpropagation.

Calculations and steps present in this method:

Forward propagation:

For each input data point, it computes the weighted sums and applies the activation function to the hidden layer.

Backpropagation:

It computes the error by prorogation through the neural network in reverse. It calculates the error in hidden layers based on the output error.

Weight updation:

It is related to the gradient descent concept. It updates weights between the input and hidden layers based on the error, which is calculated in the previous step.

Iterations:

Iterations are based on epochs where, the entire dataset is trained again in each iteration. It makes the model adjust itself with the weights.

Predict function:

Parameters used in the function:

One vector that has the input features for making predictions.

Return type:

It returns the prediction of the neural networks.

Variables present in the function are:

hiddenOutput: Vector that stores the output of the hidden layer neurons after applying activation function sigmoid. The weightedSum and output are the variables used for prediction.

calculation: For each neuron in the hidden layer (weights_input_hidden.size() number of neurons):

Iterate through the input features and calculate the weighted sum (weightedSum) by multiplying each input feature with its corresponding weight in the hidden layer.

Apply the sigmoid activation function to the weightedSum to obtain the output of the neuron.

Store the sigmoid output in the hiddenOutput vector.

calculateMeanSquaredError function:

The parameters passed to the function are:

predictedOutputs: It is a vector that contains the predicted output values, which are predicted by the neural networks.

actualOutputs: It is a vector that contains the actual values for the same inputs

return types of the function are:

it represents the calculated mean squared error between the predicted and actual outputs

Calculations:

The function first checks if the predictedOutputs and actualOutputs vectors have the same size. If they don't have the same size, an error message is printed to the standard error stream (cerr), and the function returns -1.0 to indicate an error.

The function checks if the input vectors have the same size, calculates the squared errors between predicted and actual values, computes the mean of these squared errors, and returns the mean squared error as a measure of the prediction accuracy of the neural network

main function:

This function is divided into five parts that are:

• data generation
• test data generation
• neural network initialization and training
• testing the trained neural networks
• prediction using user input

Data Generation:

This part contains two vectors named inputs, which is 2D vector and outputs, which is 1D. Now, we are making the datasets consisting of two input features and one output feature. The dataset contains 500 data points. The inputs are pushed into the inputs vector, and outputs, which are obtained by applying the relationship, are stored in the outputs vector.

Neural Network Initialization and Training:

A neural network with 2 input features, 16 hidden neurons, and 1 output neuron is used here. Now, the train method is called with four parameters, which are input vector, output vectors, number of epochs, and learning rate.

Testing the Trained Neural Network:

The trained neural network is tested on the test dataset. Predictions are made for each test data point using the prediction method. Predicted and actual outputs are printed for each test data point. Mean Squared Error (MSE) is calculated using the predicted and actual outputs to evaluate the model's performance.

Prediction using user input:

The user can input custom data (in this case, {100, 100}). The neural network makes a prediction using the trained model for the provided input features, and the predicted output is displayed.

Conclusion:

The neural network architecture comprises an input layer with 2 features: a hidden layer housing 16 neurons and an output layer with a single neuron. This model is trained using a dataset containing 500 data points, each characterized by 2 input features and 1 corresponding output value. Through backpropagation, the network adjusts its weights to minimize the disparity between predicted and actual outputs during the training phase.

Following training, the network's performance is evaluated using a separate test dataset comprising 99 data points. The Mean Squared Error (MSE) metric is employed to quantify the accuracy of the predictions. MSE measures how well the neural network captures the underlying patterns in the data, with lower MSE values indicating more accurate predictions.

It is important to note that several factors influence the effectiveness of the neural network. The random initialization of weights can affect the convergence of the training algorithm, and the dataset's quality and quantity significantly impact the model's ability to generalize to unseen data. Additionally, the number of training epochs and the learning rate are crucial hyperparameters influencing the network's performance. Fine-tuning these parameters and experimenting with different network architectures can enhance the accuracy of predictions.

Moreover, the neural network is a versatile tool that can be applied to various real-world problems, but not limited to image recognition, natural language processing, and financial forecasting. This implementation is a foundational understanding of neural networks and can be further extended and optimized for more complex tasks and datasets.