The Great Tree List Recursion Problem in C++

In this article, we will discuss the great tree list problem in C++ with several examples.

Introduction:

Think of a program that determines a number's factorial. This function takes a number N as an input and returns the factorial of N as a result. This function's pseudo-code will resemble:

Example:

#include <iostream>
using namespace std;

int sumOfNaturalNumbers(int n) {
    // Base case
    if (n == 1) {
        return 1;
    }

    // Recursive step
    return n + sumOfNaturalNumbers(n - 1);
}

int main() {
    int n = 5; // Calculate the sum of natural numbers from 1 to 5
    int result = sumOfNaturalNumbers(n);
    cout << "Sum of natural numbers from 1 to " << n << " is: " << result << endl;
    return 0;
}

Output:

Sum of natural numbers from 1 to 5 is: 15

Explanation:

Recursion is exemplified by the function that was previously mentioned. We are invoking a function to determine a number's factorial. After that, this function calls itself with a lesser value of the same number. It continues until we reach the base case, in which there are no more function calls.
Recursion is a technique for handling complicated issues when the outcome is dependent on the outcomes of smaller instances of the same issue.
If we think about functions, a function is said to be recursive if it keeps calling itself until it reaches the base case.
Any recursive function has two primary components: the base case and the recursive step.
We stop going to the recursive phase once we reach the base case. Base cases must be carefully defined and are crucial to prevent infinite recursion. The definition of infinite recursion is a recursion that never reaches the base case. If a program never reaches the base case, stack overflow will continue to occur.

Recursion Types:

There are mainly two different types of recursion:

Linear Recursion
Tree Recursion

1. Linear Recursion:

A function that calls itself just once each time it executes is said to be linear recursive. A good illustration of linear recursion is the factorial function. The name "linear recursion" refers to the fact that a linearly recursive function takes a linear amount of time to execute.

Example:

Let's take a look at the pseudo-code below:

#include <iostream>
using namespace std;

void countdown(int n) {
    // Base case to stop recursion
    if (n == 0) {
        return;
    }

    // Print the current value
    cout << n << " ";

    // Recursive step
    countdown(n - 1);
}

int main() {
    int n = 5; // Countdown from 5 to 0
    cout << "Countdown: ";
    countdown(n);
    cout << endl;
    return 0;
}

Output:

Countdown: 5 4 3 2 1

Explanation:

In this example, the simplest scenario is when n equals 0. The recursion comes to an end when n equals 0. Following this point, the function stops making recursive calls.
The function prints the current value of n at the end of each iteration. We can represent printing as a constant-time operation using the symbol K.

Let's define the temporal complexity's recurrence relation now:

T(n) = T(n - 1) + K

When the function is called with the value n as an argument, T(n) denotes the amount of time needed to complete the entire computation.
The time needed for the recursive call with n - 1 is denoted by T(n - 1).
K stands for the fixed amount of time needed to print the value of n.

According to this recurrence relation, the time needed to execute the function with parameter n is equal to the time needed for the recursive call with n - 1, plus a fixed time K for printing the value of n. In this scenario, the function is inadvertently called n times.

Since this code's time complexity is O(n), the amount of time needed to complete it is linear in terms of n. The function receives n calls, and each one executes a fixed amount of work.

2. Tree Recursion:

When you make a recursive call in your recursive case more than once, it is referred to as tree recursion. An effective illustration of Tree recursion is the fibonacci sequence. Tree recursive functions run in exponential time; they are not linear in their temporal complexity.

Example:

Take a look at the pseudo-code below,

function sumTree(node) {
  if (node === null) {
    return 0; // Base case: an empty tree has a sum of 0
  }

  // Recursive step: sum the current node's value with the sums of its left and right subtrees
  return node.value + sumTree(node.left) + sumTree(node.right);
}

// Define a simple binary tree structure
class TreeNode {
  constructor(value, left = null, right = null) {
    this.value = value;
    this.left = left;
    this.right = right;
  }
}

// Create a sample binary tree
const tree = new TreeNode(1,
  new TreeNode(2,
    new TreeNode(3),
    new TreeNode(4)
  ),
  new TreeNode(5,
    null,
    new TreeNode(6)
  )
);

// Calculate the sum of all values in the tree
const treeSum = sumTree(tree);
console.log("Sum of tree values: " + treeSum);

Output:

Sum of tree values: 21

Explanation:

In this example, with the exception of one additional call to the same function with a lower value of n, this function sumtree(n) is nearly identical to the previous one.
Let's write T(n) = T(n-1) + T(n-2) + k for this function's recurrence relation. Here, K is still another constant.
When a function is called more than once with smaller values, this sort of recursion is known as a tree recursion.

How does the recursion tree method work?

The recursion tree strategy is used to solve recurrence relations such as T(N)=T(N/2)+N or the two we previously discussed(linear recursion and Tree recursion) in the types of recursion section. The usual approach used by these recurrent relations to deal with issues is divide and conquer.

It takes time to integrate the answers to the smaller subproblems that are created when a larger problem is broken down into smaller subproblems.

For instance, T(N)=2T(N/2)+O(N) is the recurrence relation for the Merge sort. The time needed to combine the answers to two subproblems with a combined size of T(N/2) is O(N), which is true at the implementation level as well. In the merge step of the Merge sort, we combine two sorted arrays to create a new sorted array in linear time.

For instance, the recurrence relation for binary search is T(N)=T(N/2)+1, and we are aware that each repetition of a binary search cuts the search space in half. Once the outcome is determined, we exit the function. Because this is a constant time operation, + 1 +1 is added to the recurrence relation.

Take the recurrence relation T(n)=2T(n/2)+Kn into consideration. Kn denotes the amount of time required to combine the answers to n/2-dimensional subproblems.

Let's depict the recursion tree for the aforementioned recurrence relation.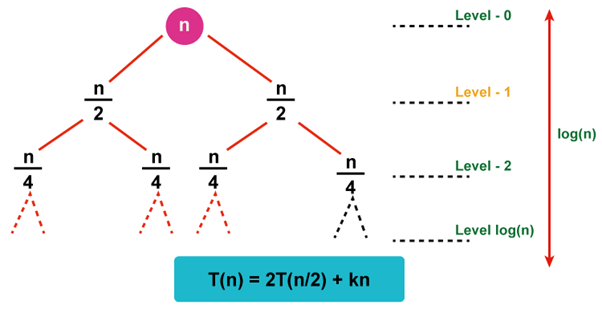

The Great Tree List Recursion Problem in C++

We may draw a few conclusions from studying the recursion tree above, including:

The size of the problem at each level is all that matters when determining the value of a node. The issue size is n at level 0, n/2, and n/2 at level 1, etc.
In general, we define the height of the tree as equal to log(n), where n is the size of the problem, and the height of this recursion tree is equal to the number of levels in the tree. It is true because as we just established, the divide-and-conquer strategy is used by recurrence relations to solve problems, and getting from problem size n to problem size 1 only requires taking log(n)
At each level, we consider the second term in the recurrence to be the root.
Even though this method's name contains the word "tree", we don't need to be an expert on trees to comprehend it.

How to Use a Recursion Tree to Solve Recurrence Relations:

The cost of the subproblem is the amount of time needed to solve it in the recursion tree approach. Therefore, the time needed to solve a subproblem is all that is meant when the word "cost" is found connected with the recursion tree.

Using the recursion tree approach, there are a few stages that must be taken to solve a recurrence relation. Including,

Draw the recursion tree to represent the given recurrence relation.
The recursion tree's height should be calculated.
Calculate the cost (amount of time needed to solve each level's subproblems) for each level.
Determine how many nodes there are overall in the recursion tree at each level.
The recursion tree's costs are totaled across all of its tiers.

Conclusion:

Recursion is a technique for handling complicated issues when the outcome is dependent on the outcomes of smaller instances of the same issue.
Linear recursion and Tree recursion are the two main types of recursion.
The Recursion tree method is one of many approaches for solving recurrence relations.
These recurrence relations are essentially just a mathematical definition of a recursive problem. The recursion tree method has a few stages that must be taken to solve a recurrence relation.