Knapsack Problem in C++

The knapsack problem is a well-known optimization problem in the fields of computing and mathematics. Considering being given a collection of objects, each with a certain weight and worth, and a backpack with a restricted weight capacity. The goal is to choose which objects to load into the backpack such that their overall worth can be maximized but the total weight is below the capacity of the rucksack. In other words, you want to choose the goods that are the most valuable given the weight restriction.

This topic has several real-world applications, including resource allocation, portfolio optimization, and production scheduling. Making the best choices across a range of fields depends on effectively solving it. The knapsack problem comes in several forms, such as the fractional knapsack problem and the 0/1 knapsack problem, where objects can be split into smaller portions to take. The knapsack problem is a key issue in optimization, and researchers have developed algorithms and methods to discover ideal or approximation solutions.

Applications of Knapsack Problem

1. Investment and Finance:
   
   • Portfolio Optimisation: The Knapsack problem is used in finance to pick the right mix of assets (stocks, bonds, etc.) to maximize returns while taking risk considerations such as spending limits or risk tolerance into account.
2. Production and Manufacturing:
   
   • Cutting Stock Problem: To satisfy customer demands while minimizing waste, industries including paper, textiles, and metal fabrication employ the Knapsack problem to identify the most effective way to cut raw materials (rolls of paper, fabric, or metal) into smaller pieces.
3. Resource Management:
   
   • Resource Allocation: The Knapsack problem can be used to represent many resource allocation scenarios, such as allocating limited assets across numerous projects or allocating bandwidth in network management to maximize resource utilization.
4. Retail and Merchandising:
   
   • Shelf Space Optimisation: Retailers employ the Knapsack problem to choose which goods to show on constrained shelf space, taking into account elements including product demand, shelf space availability, and profit margins.
5. Data Compression:
   
   • Data Compression methods: To reduce the size of data files while minimizing information loss, data compression techniques employ variants of the Knapsack problem.

Solutions for the Knapsack Problem

Several algorithms in C++ may be used to solve the Knapsack issue. Here are a few common methods:

1. Brute Force (Recursive):
   
   • This is a basic technique in which all conceivable combinations of goods are generated and checked to see which combination fits inside the capacity of the Knapsack while maximizing overall value.
   • It uses a recursive function that considers all options (to take or not take an item) and chooses the one with the highest value. Although it has a straightforward conceptual basis, its exponential temporal complexity prevents it from being effective for massive data sets.
2. Dynamic Programming:
   
   • The dynamic programming method involves the creation of a 2D array to store temporary results. The 0/1 Knapsack problem is effectively solved by eliminating irrelevant calculations.
   • The goal is to continuously fill the array, taking into account each element individually and figuring out the highest value that can be achieved given the available capacity. This method has an O(nW) time complexity, where W is the capacity and n is the number of objects.
3. Greedy algorithms:
   
   • Greedy algorithms provide representations of solutions by selecting options that are locally ideal at each stage. The fractional knapsack issue involves choosing things depending on the value-to-weight ratios of those objects.
   • Although greedy algorithms are effective and can be helpful when a quick, close-to-optimal solution is acceptable, they cannot guarantee an optimal solution for the 0/1 Knapsack issue.
4. Bound and Branch:
   
   • The algorithmic technique known as Branch and Bound combines elements from greedy and brute force methods.
   • It reduces the search space by reducing search tree branches that cannot lead to an ideal result.
   • The 0/1 Knapsack issue is frequently solved using this approach, which works well in situations of intermediate scale.
5. Genetic Algorithms:
   
   • Genetic algorithms are a systematic technique that is affected by the process of natural selection.
   • Through the evolution of a population of solutions over numerous generations, they may be used to solve combinatorial optimization issues like the Knapsack problem.
   • Although this approach can only sometimes lead to the best answer, it has the potential to do so when dealing with challenging issues.

Best Approach to Solve the Knapsack Problem

The best approach varies depending on the individual Knapsack problem type, the size of the problem instance, and whether an exact or approximate solution is required. Smaller instances of the 0/1 Knapsack are best handled by dynamic programming.

However, bigger instances and fractional Knapsack can be effectively handled using greedy and approximation techniques. When optimality is desired, branch and bound are helpful, but they may only be feasible for some big problems. For investigating intricate, substantial Knapsack issues, heuristic techniques are useful.

The Dynamic Programming strategy, particularly for the 0/1 Knapsack problem, is one of the most well-known and frequently employed solutions for the Knapsack problem. This method is recommended for its effectiveness and capacity to identify the best answer.

Knapsack problem using Dynamic Programming

Dynamic Programming (DP) is an effective approach for dealing with large problems by breaking them into smaller, simple subproblems and solving each subproblem only once. The answers to the subproblems are then stored in a table (often an array or matrix) to prevent repeated calculations. When trying to choose the best option from a list of alternatives for optimization challenges like the Knapsack problem, DP can be quite helpful.

Example:

Output: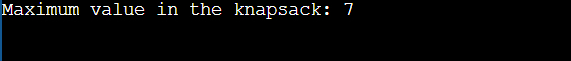

Explanation:

This program uses dynamic programming to solve this problem. Using the initial i items and a knapsack capacity of j, it uses a two-dimensional vector named dp, where dp[i][j] indicates the highest value that may be obtained. Each item and capacity combination is iterated through, and the algorithm determines the maximum value by evaluating whether or not incorporating the current item would be helpful. It uses a simple recurrence relation, comparing the highest value with and without the item and choosing the higher of the two if the weight of the current item fits inside the knapsack limit.

If the weight is more than the limit, the previous value will be carried forward. The code then returns the highest possible number, which is equivalent to the best answer to the 0/1 Knapsack problem.

This code offers an effective and well-liked response to a fundamental optimization issue. With limited resources that must be carefully managed to maximize results, its dynamic programming technique may be used in a variety of real-world settings, including resource allocation, financial portfolio optimization, and project scheduling.

Conclusion

The Knapsack issue is a well-known optimization problem with a variety of real-world applications, which makes briefly. It involves selecting components with corresponding weights and values in order to maximize the overall value while taking into account a capacity restriction. Numerous algorithms and methods have been created to address the problem's many variations, including the 0/1 Knapsack and fractional Knapsack.

The 0/1 Knapsack issue is solved using dynamic programming, which is a basic and effective method for locating the best answer. Dynamic programming is demonstrated in the corresponding C++ code. This problem-solving approach goes above Knapsack and is frequently applied in other areas of study, such as computer science, operations research, finance, and engineering, to solve resource allocation, budgeting, scheduling, and other decision-making issues.

Overall, the Knapsack problem demonstrates the importance of optimization and algorithmic strategies in addressing complex real-world issues, making it a foundational topic in computer science and mathematics.