How to read a tape measureA tape measure, also known as measuring tape, is usually a flexible tape used to measure length. Generally, tape measures are built from different materials, like plastic, fiberglass, and cloth. When we talk about the constructional work and craftsmanship, it is among the most effective measuring tools used nowadays. The concept of measuring tape basically originated in tailoring with a cloth tape, which is used to alter the cloths. Tape measures available in metric (meters and centimeters) as well as Imperial units (feet's and inches), showing zero error and work with greater efficiency. In this tutorial, we will discuss how to read a tape measure by using the Imperial and Metric unit. Method 1Tape ReadingImperial unitsConsider the numeric number for inches: On the tape measure marked with imperial units, you will find the most significant marks are commonly the 1-inch marks. These are usually marked by long thin lines and represented by the large numeric value. 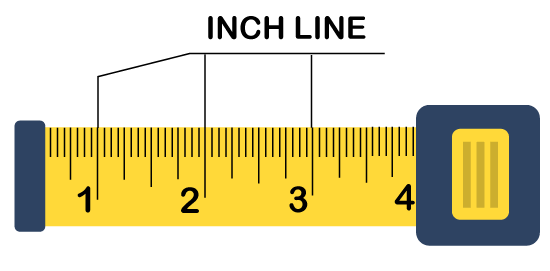
In every 12 inches, you will often find a foot marking usually shown by a different color (mostly red) than the other marking (black). Here, after a one-foot marking, you will see the numbers located next to the one-inch mark will repeat itself from 1-11 again. Consider the bigger marks between two-inch markings for half-inches: In a measuring tape, you will always find a half-inch mark is always lies between any two one-inch marks. It is the second-longest marking shown on the measuring tape after the one-inch marks. In the measuring tape, you will see each half-inch marks lie between each once inch marks, but it has two half inches between 1 inch. 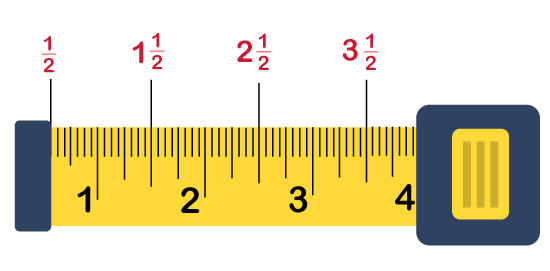
If you start with half-inch marks, it might be possible not all the lines are shown with numbers. In this case, you can use the marker to write on either side for help. For example, the half-inch marks lie between 2 and 3 stands for two and ½ inches, even though it is not shown. Consider the smaller lines lies between the half inches for quarter inches: Quarter inches are smaller or thinner than the half inches but commonly bigger than the densely-packed marks. You will always find the quarter inches are evenly distributed between each half inches mark and one inch-mark, so there is a 4 quarter inch mark in one inch. 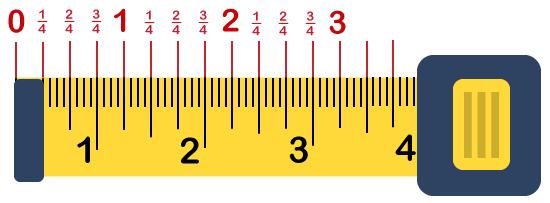
Consider the small marks for one-eight inches: One eighth inch markings are smaller than the quarter and one-inch markings. The markings lie between the center of one-inch marking and quarter-inch marking, the quarter-inch marking and the half-inch marking, and so on. There are eight one-eighth inches per inch. 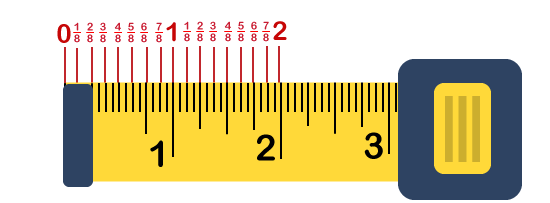
Consider the tiny marks for sixteenths of an inch: Sixteenth-inch marks are considered as the shortest lines of all measuring tapes. You will find 16 tiny marks per inches and 4 in each quarter inch. 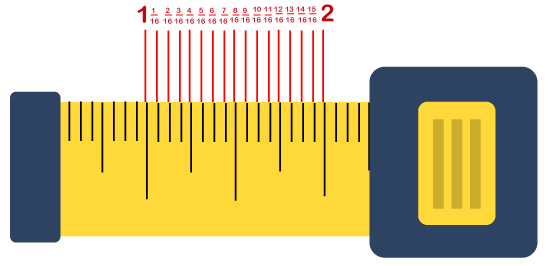
Sum up the distribution of inches to evaluate the total length: If you are going to calculate a specific length, evaluating correct results, just means seeing where the tape touches. Firstly, you need to highlight the spot where the measuring tape touches with the outline of the thing you are measuring. Afterward, calculate the closest inch before this specific point. Then, calculate the nearest half-inch before this point. Afterward, calculate the closest quarter inch before this point, and so on. Sum up all the inches and fractions of inches until you find the correct result. 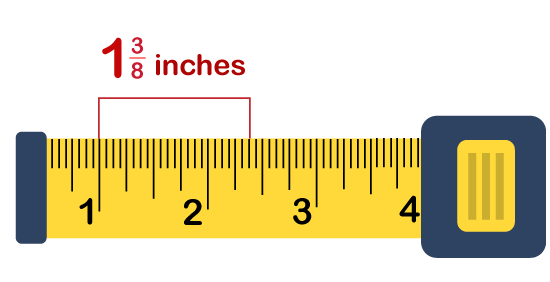
Let us suppose we have measured past the two-inch mark, past the one-quarter-inch mark, and past one eighth inch mark. So, if we want to calculate our measurement, we need to add on 2 (inches) + 1/4 (Quarter inches) + 1/8 (Eighth inches). As we know that, in measuring tape, there are two eighth-inches in a quarter-inch mark so that we can rewrite this equation as: 2 + 2/8 + 1/8 = 21/8 inches. Imperial unitsConsider the numeric number for centimeters: In metric measuring tapes, centimeters are the most significant markings. Centimeters are generally represented by the large lines (shown by black color), and you will see a number next to each line. Same as inches, the line represents each centimeter. 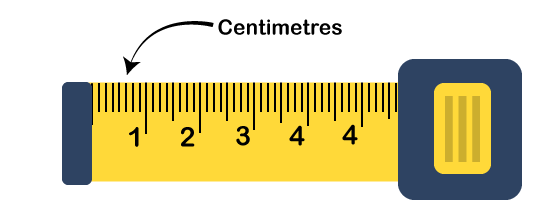
Generally, we use measuring tape with one-meter length (100 centimeters), where we will get a specific marking for the meter. (Represented by a different color). After each meter, you will see the centimeter markings repeat itself again from zero. It varies from one measuring tape to another measuring tape. Consider the smaller marking between the centimeters as 0.5 centimeters: In some measuring tapes (Metric), medium-sized marks are evenly distributed between each centimeter mark. These marks represented the half centimeters mark, and usually not shown with a number. 
We know that the base of the metric system is 10, so it makes it is easy to calculate the result with the decimal system as compared to imperial measuring tape. This is the significant reason; it is normally best to refer to half centimeter markings in decimal terms. For example, 2 ½ centimeters will be considered as 2.5 centimeters. Consider the tiny markings as millimet The tiny, narrow lines represent the millimeters located between the centimeter markings. The millimeter can also be considered as one-tenth centimeters. As we know, 1 centimeter is equal to 10 millimeters, whereas one thousand millimeters is equal to a meter. 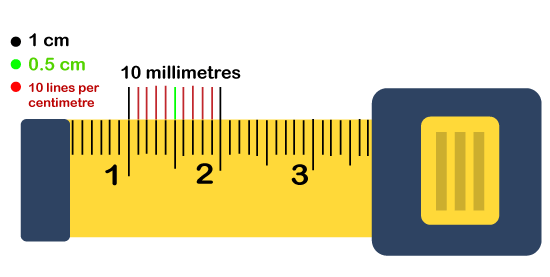
In some conditions, you will find the tape measure doesn't show a half-centimeter markings, where you have to assume the fifth-millimeter markings after each centimeter marks as 0.5 centimeters. Add on the centimeter distributions to calculate the total length: If you measure anything with the metric measuring tape, firstly, you need to find the closest centimeter before the distance you are going to measure, afterward the closest millimeter. You can also use a half-millimeter marking for help if your measuring tape has them. 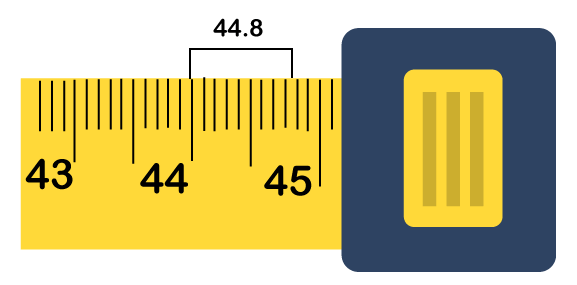
Let's understand this concept with the help of an example. Let us consider that we measure the past 44-centimeter mark to the 8-millimeter mark. In this particular case, we need to find our distance in centimeter like: 44 + 0.8 = 44.8 centimetres If we want our distance in other units (other than centimeters), we need to shift the decimal place to satisfy the other units. For example, if you want the result in meters, you need to use a conversion formula, as we know that one meter equals 100 centimeters. We will get the equation like 44.8 × 1 metre/100 centimetres = 0.448 metres. If you want to converse the final value from centimeter to meters, you need to move the decimal value two places towards the left side. If you want to converse the final value-form meters to centimeters, you need to shift the decimal value two places towards the right side.
Next TopicHow to Reset Instagram Password
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










