THE DINING PHILOSOPHERS PROBLEM

The dining philosopher's problem is the classical problem of synchronization which says that Five philosophers are sitting around a circular table and their job is to think and eat alternatively. A bowl of noodles is placed at the center of the table along with five chopsticks for each of the philosophers. To eat a philosopher needs both their right and a left chopstick. A philosopher can only eat if both immediate left and right chopsticks of the philosopher is available. In case if both immediate left and right chopsticks of the philosopher are not available then the philosopher puts down their (either left or right) chopstick and starts thinking again.

The dining philosopher demonstrates a large class of concurrency control problems hence it's a classic synchronization problem.

Five Philosophers sitting around the table

Dining Philosophers Problem- Let's understand the Dining Philosophers Problem with the below code, we have used fig 1 as a reference to make you understand the problem exactly. The five Philosophers are represented as P0, P1, P2, P3, and P4 and five chopsticks by C0, C1, C2, C3, and C4.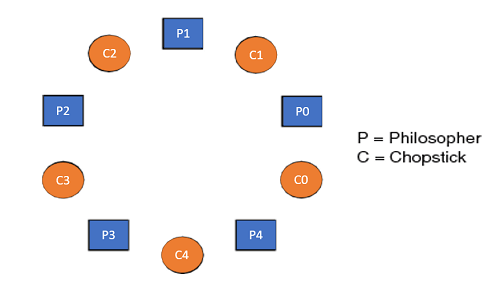

Let's discuss the above code:

Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C0 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1)

Similarly suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C1 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C2 chopstick( since i =1, therefore (1 + 1) % 5 = 2)

But Practically Chopstick C1 is not available as it has already been taken by philosopher P0, hence the above code generates problems and produces race condition.

The solution of the Dining Philosophers Problem

We use a semaphore to represent a chopstick and this truly acts as a solution of the Dining Philosophers Problem. Wait and Signal operations will be used for the solution of the Dining Philosophers Problem, for picking a chopstick wait operation can be executed while for releasing a chopstick signal semaphore can be executed.

Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:

From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop(because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.

The structure of the chopstick is an array of a semaphore which is represented as shown below -

Initially, each element of the semaphore C0, C1, C2, C3, and C4 are initialized to 1 as the chopsticks are on the table and not picked up by any of the philosophers.

Let's modify the above code of the Dining Philosopher Problem by using semaphore operations wait and signal, the desired code looks like

In the above code, first wait operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows philosopher i have picked up the chopsticks from its left and right. The eating function is performed after that.

On completion of eating by philosopher i the, signal operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows that the philosopher i have eaten and put down both the left and right chopsticks. Finally, the philosopher starts thinking again.

Let's understand how the above code is giving a solution to the dining philosopher problem?

Let value of i = 0( initial value ), Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C0 chopstick and reduces semaphore C0 to 0, after that it execute Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1) and reduces semaphore C1 to 0

Similarly, suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it will try to hold C1 chopstick but will not be able to do that, since the value of semaphore C1 has already been set to 0 by philosopher P0, therefore it will enter into an infinite loop because of which philosopher P1 will not be able to pick chopstick C1 whereas if Philosopher P2 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C2 chopstick and reduces semaphore C2 to 0, after that, it executes Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C3 chopstick( since i =2, therefore (2 + 1) % 5 = 3) and reduces semaphore C3 to 0.

Hence the above code is providing a solution to the dining philosopher problem, A philosopher can only eat if both immediate left and right chopsticks of the philosopher are available else philosopher needs to wait. Also at one go two independent philosophers can eat simultaneously (i.e., philosopher P0 and P2, P1 and P3 & P2 and P4 can eat simultaneously as all are the independent processes and they are following the above constraint of dining philosopher problem)

The drawback of the above solution of the dining philosopher problem

From the above solution of the dining philosopher problem, we have proved that no two neighboring philosophers can eat at the same point in time. The drawback of the above solution is that this solution can lead to a deadlock condition. This situation happens if all the philosophers pick their left chopstick at the same time, which leads to the condition of deadlock and none of the philosophers can eat.

To avoid deadlock, some of the solutions are as follows -

• Maximum number of philosophers on the table should not be more than four, in this case, chopstick C4 will be available for philosopher P3, so P3 will start eating and after the finish of his eating procedure, he will put down his both the chopstick C3 and C4, i.e. semaphore C3 and C4 will now be incremented to 1. Now philosopher P2 which was holding chopstick C2 will also have chopstick C3 available, hence similarly, he will put down his chopstick after eating and enable other philosophers to eat.
• A philosopher at an even position should pick the right chopstick and then the left chopstick while a philosopher at an odd position should pick the left chopstick and then the right chopstick.
• Only in case if both the chopsticks ( left and right ) are available at the same time, only then a philosopher should be allowed to pick their chopsticks
• All the four starting philosophers ( P0, P1, P2, and P3) should pick the left chopstick and then the right chopstick, whereas the last philosopher P4 should pick the right chopstick and then the left chopstick. This will force P4 to hold his right chopstick first since the right chopstick of P4 is C0, which is already held by philosopher P0 and its value is set to 0, i.e C0 is already 0, because of which P4 will get trapped into an infinite loop and chopstick C4 remains vacant. Hence philosopher P3 has both left C3 and right C4 chopstick available, therefore it will start eating and will put down its both chopsticks once finishes and let others eat which removes the problem of deadlock.

The design of the problem was to illustrate the challenges of avoiding deadlock, a deadlock state of a system is a state in which no progress of system is possible. Consider a proposal where each philosopher is instructed to behave as follows:

• The philosopher is instructed to think till the left fork is available, when it is available, hold it.
• The philosopher is instructed to think till the right fork is available, when it is available, hold it.
• The philosopher is instructed to eat when both forks are available.
• then, put the right fork down first
• then, put the left fork down next
• repeat from the beginning.