Tasks in Real-Time SystemsA real-time operating system (RTOS) serves real-time applications that process data without any buffering delay. In an RTOS, the Processing time requirement is calculated in tenths of seconds increments of time. It is a time-bound system that is defined as fixed time constraints. In this type of system, processing must be done inside the specified constraints. Otherwise, the system will fail. Real-time tasks are the tasks associated with the quantitative expression of time. This quantitative expression of time describes the behavior of the real-time tasks. Real-time tasks are scheduled to finish all the computation events involved in it into timing constraint. The timing constraint related to the real-time tasks is the deadline. All the real-time tasks need to be completed before the deadline. For example, Input-output interaction with devices, web browsing, etc. Types of Tasks in Real-Time SystemsThere are the following types of tasks in real-time systems, such as: 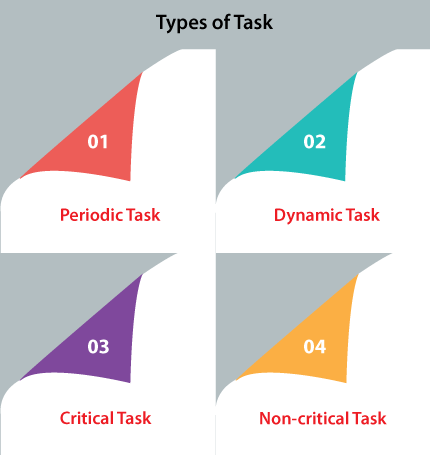
1. Periodic Task In periodic tasks, jobs are released at regular intervals. A periodic task repeats itself after a fixed time interval. A periodic task is denoted by five tuples: Ti = < Φi, Pi, ei, Di > Where,
For example: Consider the task Ti with period = 5 and execution time = 3 Phase is not given so, assume the release time of the first job as zero. So the job of this task is first released at t = 0, then it executes for 3s, and then the next job is released at t = 5, which executes for 3s, and the next job is released at t = 10. So jobs are released at t = 5k where k = 0, 1. . . N 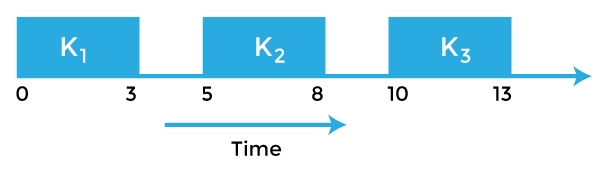
Hyper period of a set of periodic tasks is the least common multiple of all the tasks in that set. For example, two tasks T1 and T2 having period 4 and 5 respectively will have a hyper period, H = lcm(p1, p2) = lcm(4, 5) = 20. The hyper period is the time after which the pattern of job release times starts to repeat. 2. Dynamic Tasks It is a sequential program that is invoked by the occurrence of an event. An event may be generated by the processes external to the system or by processes internal to the system. Dynamically arriving tasks can be categorized on their criticality and knowledge about their occurrence times.
3. Critical Tasks Critical tasks are those whose timely executions are critical. If deadlines are missed, catastrophes occur. For example, life-support systems and the stability control of aircraft. If critical tasks are executed at a higher frequency, then it is necessary. 4. Non-critical Tasks Non-critical tasks are real times tasks. As the name implies, they are not critical to the application. However, they can deal with time, varying data, and hence they are useless if not completed within a deadline. The goal of scheduling these tasks is to maximize the percentage of jobs successfully executed within their deadlines. Task SchedulingReal-time task scheduling essentially refers to determining how the various tasks are the pick for execution by the operating system. Every operating system relies on one or more task schedulers to prepare the schedule of execution of various tasks needed to run. Each task scheduler is characterized by the scheduling algorithm it employs. A large number of algorithms for real-time scheduling tasks have so far been developed. Classification of Task SchedulingHere are the following types of task scheduling in a real-time system, such as: 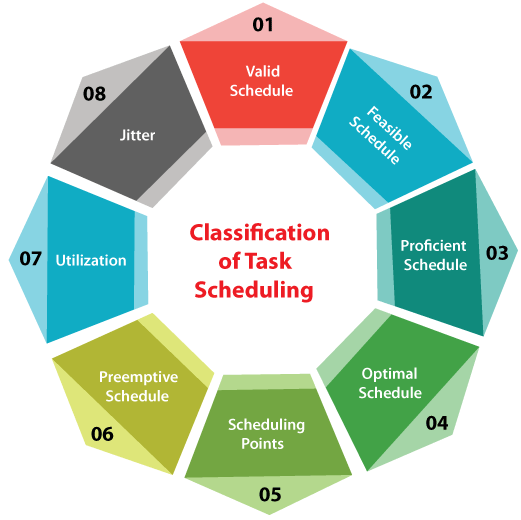
Precedence Constraint of JobsJobs in a task are independent if they can be executed in any order. If there is a specific order in which jobs must be executed, then jobs are said to have precedence constraints. For representing precedence constraints of jobs, a partial order relation < is used, and this is called precedence relation. A job Ji is a predecessor of job Jj if Ji < Jj, i.e., Jj cannot begin its execution until Ji completes. Ji is an immediate predecessor of Jj if Ji < Jj, and there is no other job Jk such that Ji < Jk < Jj. Ji and Jj are independent if neither Ji < Jj nor Jj < Ji is true. An efficient way to represent precedence constraints is by using a directed graph G = (J, <) where J is the set of jobs. This graph is known as the precedence graph. Vertices of the graph represent jobs, and precedence constraints are represented using directed edges. If there is a directed edge from Ji to Jj, it means that Ji is the immediate predecessor of Jj. For example: Consider a task T having 5 jobs J1, J2, J3, J4, and J5, such that J2 and J5 cannot begin their execution until J1 completes and there are no other constraints. The precedence constraints for this example are: J1 < J2 and J1 < J5 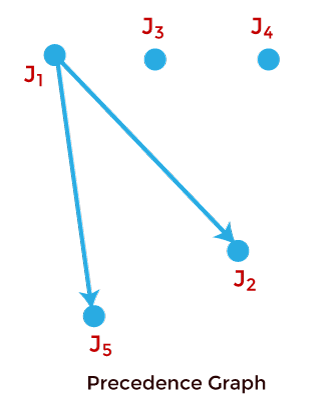
Set representation of precedence graph:
Consider another example where a precedence graph is given, and you have to find precedence constraints. 
From the above graph, we derive the following precedence constraints:
Next TopicWhat is RPC in Operating System
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









