What is Buddy System?The two smaller parts of the block are of equal size and called buddies. The buddy system is a procedure in which two individual buddies operate together as a single unit so that they can monitor and help each other. Similarly, one of the two buddies will further divide into smaller parts until the request is fulfilled. Merriam-Webster is the first known use of the phrase buddy system in 1942. According to Webster buddy system is an arrangement in which two individuals are paired (as for mutual safety in a hazardous situation). The buddy system is basically working together in pairs in a large group or alone. Both the individuals have to do the job. The job could ensure that the work is finished safely or transferred effectively from one individual to the other. Types of Buddy SystemThere are the following four types of Buddy systems. 1. Binary Buddy System The buddy system maintains a list of the free blocks of each size (called a free list) so that it is easy to find a block of the desired size if one is available. If no block of the requested size is available, Allocate searches for the first non-empty list for blocks of atleast the size requested. In either case, a block is removed from the free list. For example, suppose the size of the memory segment is initially 256kb, and the kernel requests 25kb of memory. The segment is initially divided into two buddies. Let's say A1 and A2, each 128kb in size. One of these buddies is further divided into two 64kb buddies, B1 and B2. But the next highest power of 25kb is 32kb so, either B1 or B2 is further divided into two 32kb buddies (C1 and C2), and finally, one of these buddies is used to satisfy the 25kb request. A split block can only be merged with its unique buddy block, which then reforms the larger block they were split from. 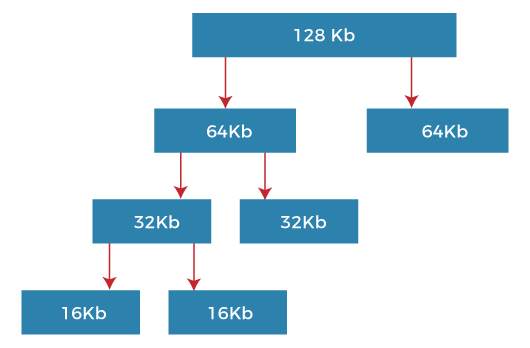
2. Fibonacci Buddy System A Fibonacci buddy system is a system in which blocks are divided into sizes which are Fibonacci numbers. It satisfies the following relation:
Zi = Z(i-1)+Z(i-2)
The original procedure for the Fibonacci buddy system was either limited to a small, fixed number of block sizes or a time-consuming computation. 3. Weighted Buddy System The weighted buddy system is similar to the original buddy system. The large blocks are split iteratively to provide the desired smaller blocks in this system. When blocks are released, they are combined with their buddy if the buddy is available or, failing this, are attached to an available space list. The binary and weighted buddy system has the following similarities.
4. Tertiary Buddy System The tertiary buddy system allows block sizes of 2k and 3.2 k, whereas the original binary buddy system allows only block sizes of 2k. This extension is achieved at an additional cost of two bits per block. Simulation of the proposed algorithm has been implemented in the C programming language. The performance analysis in terms of internal fragmentation for the tertiary buddy system with other existing schemes such as the binary buddy system, Fibonacci buddy system, and the weighted buddy system is given in this work. Further, the comparison of simulation results for several splits and the average number of merges for the above systems is also discussed. Buddy System Memory Allocation TechniqueThe buddy system memory allocation technique is an algorithm that divides memory into partitions to satisfy a memory request as suitably as possible. This system uses splitting memory into half to give the best fit. The Buddy memory allocation is relatively easy to implement. It supports limited but efficient splitting and merging of memory blocks. Algorithm of Buddy Memory AllocationThere are various forms of the buddy system in which each block is subdivided into two smaller blocks are the simplest and most common variety. Every memory block in this system has an order, where the order is an integer ranging from 0 to a specified upper limit. The size of a block of order n is proportional to 2n so that the blocks are exactly twice the size of blocks that are one order lower. Power of two block sizes makes address computation simple because all buddies are aligned on memory address boundaries that are powers of two.
For example, if the system had 2000 K of physical memory and the order-0 block size was 4 K, the upper limit on the order would be 8 since an order-8 block (256 order-0 blocks, 1024 K) is the biggest block that will fit in memory. Consequently, it is impossible to allocate the entire physical memory in a single chunk; the remaining 976 K of memory would have to be allocated in smaller blocks. Advantages Buddy system allocation has the following advantages, such as:
Disadvantage It also has some disadvantages, such as:
Example of Buddy System Memory AllocationThe following is an example of what happens when a program makes requests for memory. Suppose in this system, the smallest possible block is 64 kilobytes in size, and the upper limit for the order is 4, which results in the largest possible allocatable block, 24 times 64 K = 1024 K in size. The following image shows a possible state of the system after various memory requests. 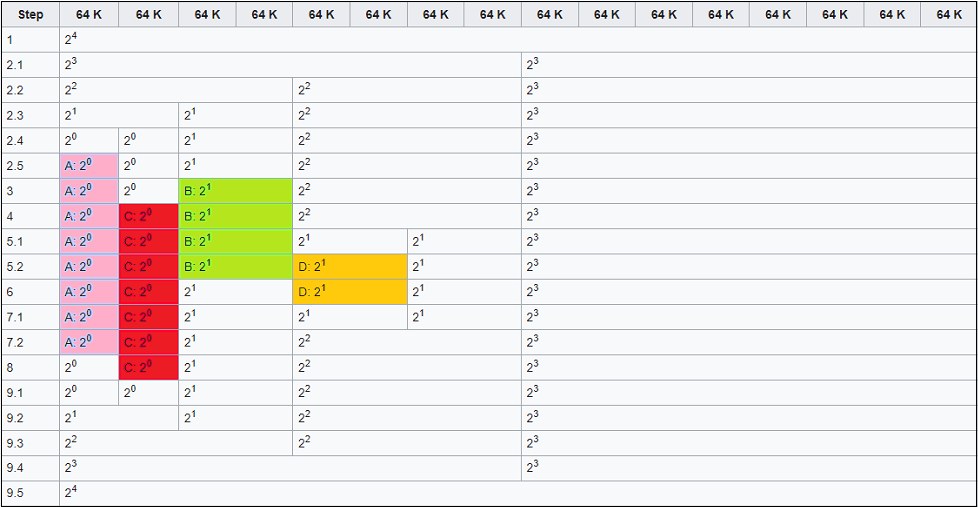
This memory allocation could have occurred in the following manner. Step 1: This is the initial situation. Step 2: Program A requests memory 34 K, order 0.
Step 3: Program B requests memory 66 K, order 1. An order 1 block is available, so it is allocated to B. Step 4: Program C requests memory 35 K, order 0. An order 0 block is available, so it is allocated to C. Step 5: Program D requests memory 67 K, order 1.
Step 6: Program B releases its memory, freeing one order 1 block. Step 7: Program D releases its memory.
Step 8: Program A releases its memory, freeing one order 0 block. Step 9: Program C releases its memory.
As you can see in the above steps, what happens when a memory request is made is as follows:
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










