Calculator using Shunting yard algorithm in HTML using JavaScript
Building a calculator is one of the first challenges to take up when learning JavaScript. We can use different methods to build a calculator like by using eval(), loops etc. There are two tutorials in the website already about how to create a calculator using eval() and using for loops. However, both of those methods aren't that efficient given the security issues the website can face because of the use of eval() and the increased complexity of the code with more number of loops. This tutorial explains one of the efficient methods we can use to build a calculator. We'll be using the Shunting Yard algorithm proposed by Dijkstra to solve the expressions in the calculator for which we'll use two stacks rather than one.
Simple Introduction to HTML, CSS and JS:
- HTML is the markup language used to structure a webpage.
- CSS is the styling language used to design the layout and look of the elements of the webpage.
- JS is the scripting language used to define the behavior and working of the elements in the webpage.
Simple introduction to Shunting Yard Algorithm:
Generally, this algorithm is used to convert an infix expression to postfix also known as Reverse Polish notation (RPN). An expression of the format a + b is an infix notation while the format ab+ is its postfix notation. Evaluating a postfix expression is easy and generally, a computer converts any given infix expression into postfix to evaluate the answer using stacks.
Steps to convert infix to Postfix:
- Read the given expression from left to right. If the scanned element is an operand, simply append it to the resultant postfix expression.
- If the scanned operator is an operator and the stack is empty, push the operator into the stack
- If the scanned element is an operator and the precedence of the operator is greater than or equal to the precedence of the operator on the top of the stack, push it into the stack
- If the scanned operator is an operator and the precedence of the scanned operator is less than the precedence of the operator on the top of the stack, pop the operator on the top of the stack and add it to the postfix expression until the stack becomes empty or the precedence of the operator on the top of the stack is less than the precedence of the scanned operator. Now, push the scanned operator into the stack.
For example: 3 + 8 - 9 / 8
| Scanned element |
Stack |
Postfix notation |
| 3 |
- |
3 |
| + |
+ |
3 |
| 8 |
+ |
3 8 |
| - |
- |
3 8 + |
| 9 |
- |
3 8 + 9 |
| / |
-/ |
3 8 + 9 |
| 8 |
-/ |
3 8 + 9 8 |
|
Postfix expression: |
3 8 + 9 8 / - |
Evaluating a postfix expression:
Example:
Take the above converted postfix notation. First let us get the result from the infix notation:
3 + 8 - 9 / 8
= 3 + 8 - 1.125
= 11 - 1.125
= 9.875
- Order of evaluation: Scientific calculator (BODMAS)
Now, let us take the postfix expression we got from the previous conversion:
3 8 + 9 8 / -
- Read the expression from left to right, initialize a stack with the same length as the expression.
- If the element encountered is an operand, push it into the stack.
- If the element encountered is an operator, pop two operands a and b from the stack, apply the operator (b operator a) and push the result back into the stack.
- In the above example: 3 8 + 9 8 / -

Now, to build a calculator using Shunting yard algorithm, we'll e using two stacks because along with converting to postfix, we also need to evaluate the postfix notation.
Sample HTML and CSS for the Calculator:
CSS:
JavaScript:
- On clicking numbers or operators, the value of the button must be displayed on the display.
- On clicking on C, the display has to become empty.
- On clicking B, the last element on the display must be deleted.
- On clicking =, everything on the display must be solved and now the display has to show the result of the expression entered.
Hence, we need to write 4 functions in JavaScript for the functionalities of four types of buttons.
You can style the calculator anyway you want using CSS. For simplicity, we aren't using much styling features. We'll create the calculator in the same design as in the tutorial where we used eval() to create the calculator.
We'll make a calculator like this:
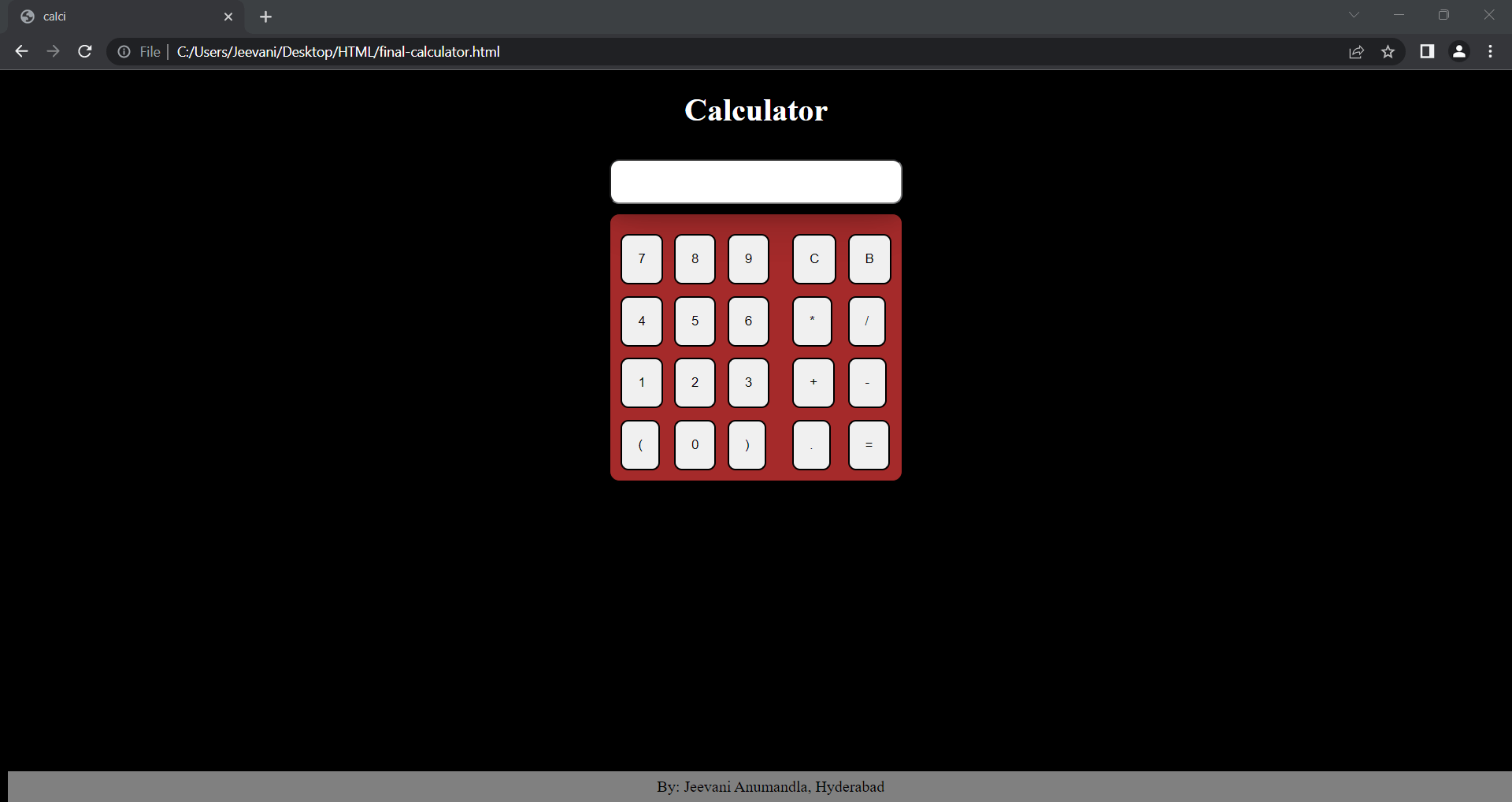
- We used io to develop the code. You can use a text editor or any software you want.
Code:
Rather than bringing out the whole code at once, let us break it down. First, the displaying part:
- fun(a):
- On clicking all the buttons of numbers and operators, we call fun () with the value of the number or operator as argument.
- In the function, we need to print that value on the display input box, hence, we concatenate the argument to the value already in the input box.
- C(): We'll simply reassign the value of the display input box to an empty string to clear the display.
- B(): We'll get the whole string on the display and slice it deleting the last element and re-assign it to the display again.
- res(): This function is activated on clicking =.
Using trim(), we're getting rid of any extra unnecessary spaces and then, the expression is given as input to another function fun1().
fun1():
This function contains the actual functionality or the backend of the calculator after taking the expression as input:
Code:
Explanation:
- We declared two arrays (stacks), values[] and operators[].
- opc and clc stand for opening braces and closing braces.
- In the next for loop, we've checked if the number of opening braces is equal to the number of closing braces. Else, it returns that the expression provided is invalid.
- According to BODMAS, we need to first solve the sub-expressions inside brackets, hence, we check if there are any brackets and if there are, we extract the sub-expression between the brackets and call fun1() again with the sub-expression as input.
- This recursion continues if there are any brackets in the expression.
- Now, coming to the actual solving part:
- We check if there is a preceding sign to the expression, if there is any, we push a 0 into values. Suppose, if expression is -8: 0-8 is still -8.
- Then, we checked if there are consecutive operators which return invalid expression again.
- If there is an operand, push it into the values stack
- Now, if there is an operator:
- If the operators stack is empty, push the operator into the stack
- If the precedence of the operator found is greater than the precedence of the operator on the top of the operators stack, push the operator into the stack
- If the precedence of the operator found is less than or equal to the operator on the top of the operators stack, pop the last operator from the operators stack and two operands from the values stack and perform the operation on the two operands and push the result into the values stack.
- Continue the process until the precedence of the operator found is greater than the precedence of the operator on the top of the stack.
- Now, we handled a situation where + and - can be consecutive. This usually occurs where there are brackets: 3 + (2 - 3) -> 3 + - 1 -> 2
- In that scenario, we get the operand along with the - sign, convert it into float and push it into values stack like a regular operand.
- Finally, if the operators stack isn't empty which means there are still a few operators and values left, pop out the operands from the values stack and apply the operator on the top of the operators stack and pop the operator from the operators stack.
- Continue the process until there are no operators and operands left in the operators and values stack.
- The function precedence is to manage the precedence rules as in BODMAS/ PEDMAS
Example:
Expression: 3 + (5 + 9 * 9)
- The expression between the parenthesis is passed again to the function:
- 5 is pushed into the values stack
- + is pushed into the operators stack
- 9 is pushed into the values stack
- The precedence of * is greater than +, so, it is pushed into the values stack
- 9 is pushed into the values stack.
Values:
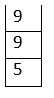
Operators:
- Pop two operands from values stack: 9 9 and apply the operator at the top of the operators stack: 9 * 9 = 81. Push 81 into the values stack:
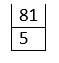
81 + 5 = 86.
- Now, 86 is concatenated to the original string in the place of the expression within parenthesis
- Expression: 3 + 86
- 3 is pushed into the values stack.
- + is pushed into the operators stack
- 86 is pushed into the values stack
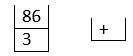
- 86 + 3 = 89 is the final result.
Output Screens:


|




 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now












