An Activity Selection ProblemThe activity selection problem is a mathematical optimization problem. Our first illustration is the problem of scheduling a resource among several challenge activities. We find a greedy algorithm provides a well designed and simple method for selecting a maximum- size set of manually compatible activities. Suppose S = {1, 2....n} is the set of n proposed activities. The activities share resources which can be used by only one activity at a time, e.g., Tennis Court, Lecture Hall, etc. Each Activity "i" has start time si and a finish time fi, where si ≤fi. If selected activity "i" take place meanwhile the half-open time interval [si,fi). Activities i and j are compatible if the intervals (si, fi) and [si, fi) do not overlap (i.e. i and j are compatible if si ≥fi or si ≥fi). The activity-selection problem chosen the maximum- size set of mutually consistent activities. Algorithm Of Greedy- Activity Selector:
GREEDY- ACTIVITY SELECTOR (s, f)
1. n ← length [s]
2. A ← {1}
3. j ← 1.
4. for i ← 2 to n
5. do if si ≥ fi
6. then A ← A ∪ {i}
7. j ← i
8. return A
Example: Given 10 activities along with their start and end time as S = (A1 A2 A3 A4 A5 A6 A7 A8 A9 A10) Si = (1,2,3,4,7,8,9,9,11,12) fi = (3,5,4,7,10,9,11,13,12,14) Compute a schedule where the greatest number of activities takes place. Solution: The solution to the above Activity scheduling problem using a greedy strategy is illustrated below: Arranging the activities in increasing order of end time  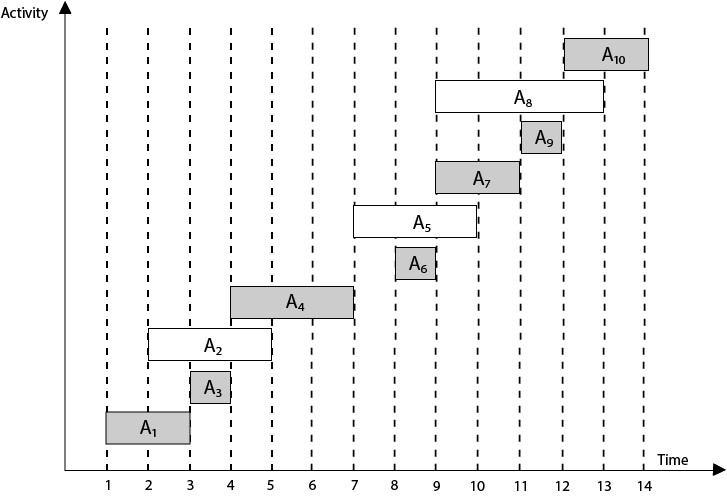
Now, schedule A1 Next schedule A3 as A1 and A3 are non-interfering. Next skip A2 as it is interfering. Next, schedule A4 as A1 A3 and A4 are non-interfering, then next, schedule A6 as A1 A3 A4 and A6 are non-interfering. Skip A5 as it is interfering. Next, schedule A7 as A1 A3 A4 A6 and A7 are non-interfering. Next, schedule A9 as A1 A3 A4 A6 A7 and A9 are non-interfering. Skip A8 as it is interfering. Next, schedule A10 as A1 A3 A4 A6 A7 A9 and A10 are non-interfering. Thus the final Activity schedule is: 
Next TopicFractional Knapsack problem
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









