Longest Common Sequence (LCS)

A subsequence of a given sequence is just the given sequence with some elements left out.

Given two sequences X and Y, we say that the sequence Z is a common sequence of X and Y if Z is a subsequence of both X and Y.

In the longest common subsequence problem, we are given two sequences X = (x₁ x₂....x_m) and Y = (y₁ y₂ y_n) and wish to find a maximum length common subsequence of X and Y. LCS Problem can be solved using dynamic programming.

Characteristics of Longest Common Sequence

A brute-force approach we find all the subsequences of X and check each subsequence to see if it is also a subsequence of Y, this approach requires exponential time making it impractical for the long sequence.

Given a sequence X = (x₁ x₂.....x_m) we define the ith prefix of X for i=0, 1, and 2...m as X_i= (x₁ x₂.....x_i). For example: if X = (A, B, C, B, C, A, B, C) then X₄= (A, B, C, B)

Optimal Substructure of an LCS: Let X = (x₁ x₂....x_m) and Y = (y₁ y₂.....) y_n) be the sequences and let Z = (z₁ z₂......z_k) be any LCS of X and Y.

• If x_m = y_n, then z_k=x_m=y_n and Z_k-1 is an LCS of X_m-1and Y_n-1
• If x_m ≠ y_n, then z_k≠ x_m implies that Z is an LCS of X_m-1and Y.
• If x_m ≠ y_n, then z_k≠y_n implies that Z is an LCS of X and Y_n-1

Step 2: Recursive Solution: LCS has overlapping subproblems property because to find LCS of X and Y, we may need to find the LCS of X_m-1 and Y_n-1. If x_m ≠ y_n, then we must solve two subproblems finding an LCS of X and Y_n-1.Whenever of these LCS's longer is an LCS of x and y. But each of these subproblems has the subproblems of finding the LCS of X_m-1 and Y_n-1.

Let c [i,j] be the length of LCS of the sequence X_iand Y_j.If either i=0 and j =0, one of the sequences has length 0, so the LCS has length 0. The optimal substructure of the LCS problem given the recurrence formula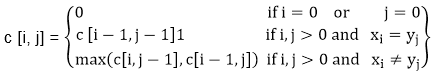

Step3: Computing the length of an LCS: let two sequences X = (x₁ x₂.....x_m) and Y = (y₁ y₂..... y_n) as inputs. It stores the c [i,j] values in the table c [0......m,0..........n].Table b [1..........m, 1..........n] is maintained which help us to construct an optimal solution. c [m, n] contains the length of an LCS of X,Y.