Asymptotic Analysis of algorithms (Growth of function)Resources for an algorithm are usually expressed as a function regarding input. Often this function is messy and complicated to work. To study Function growth efficiently, we reduce the function down to the important part. Let f (n) = an2+bn+c In this function, the n2 term dominates the function that is when n gets sufficiently large. Dominate terms are what we are interested in reducing a function, in this; we ignore all constants and coefficient and look at the highest order term concerning n. Asymptotic notation:The word Asymptotic means approaching a value or curve arbitrarily closely (i.e., as some sort of limit is taken). Asymptotic analysisIt is a technique of representing limiting behavior. The methodology has the applications across science. It can be used to analyze the performance of an algorithm for some large data set. 1. In computer science in the analysis of algorithms, considering the performance of algorithms when applied to very large input datasets The simplest example is a function ƒ (n) = n2+3n, the term 3n becomes insignificant compared to n2 when n is very large. The function "ƒ (n) is said to be asymptotically equivalent to n2 as n → ∞", and here is written symbolically as ƒ (n) ~ n2. Asymptotic notations are used to write fastest and slowest possible running time for an algorithm. These are also referred to as 'best case' and 'worst case' scenarios respectively. "In asymptotic notations, we derive the complexity concerning the size of the input. (Example in terms of n)" "These notations are important because without expanding the cost of running the algorithm, we can estimate the complexity of the algorithms." Why is Asymptotic Notation Important?1. They give simple characteristics of an algorithm's efficiency. 2. They allow the comparisons of the performances of various algorithms. Asymptotic Notations:Asymptotic Notation is a way of comparing function that ignores constant factors and small input sizes. Three notations are used to calculate the running time complexity of an algorithm: 1. Big-oh notation: Big-oh is the formal method of expressing the upper bound of an algorithm's running time. It is the measure of the longest amount of time. The function f (n) = O (g (n)) [read as "f of n is big-oh of g of n"] if and only if exist positive constant c and such that Hence, function g (n) is an upper bound for function f (n), as g (n) grows faster than f (n) 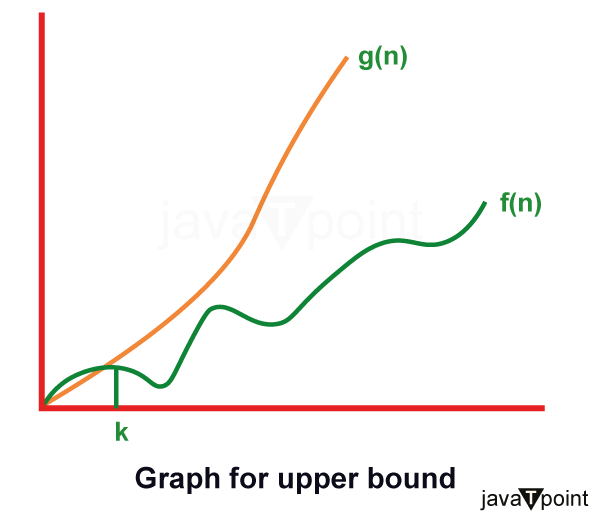
For Example:Hence, the complexity of f(n) can be represented as O (g (n)) 2. Omega () Notation: The function f (n) = Ω (g (n)) [read as "f of n is omega of g of n"] if and only if there exists positive constant c and n0 such that F (n) ≥ k* g (n) for all n, n≥ n0 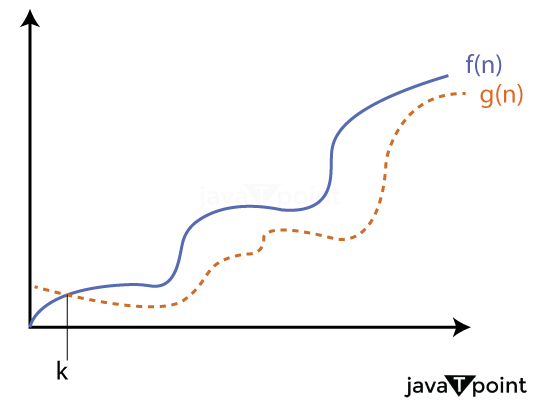
For Example:
f (n) =8n2+2n-3≥8n2-3
=7n2+(n2-3)≥7n2 (g(n))
Thus, k1=7
Hence, the complexity of f (n) can be represented as Ω (g (n)) 3. Theta (θ): The function f (n) = θ (g (n)) [read as "f is the theta of g of n"] if and only if there exists positive constant k1, k2 and k0 such that k1 * g (n) ≤ f(n)≤ k2 g(n)for all n, n≥ n0 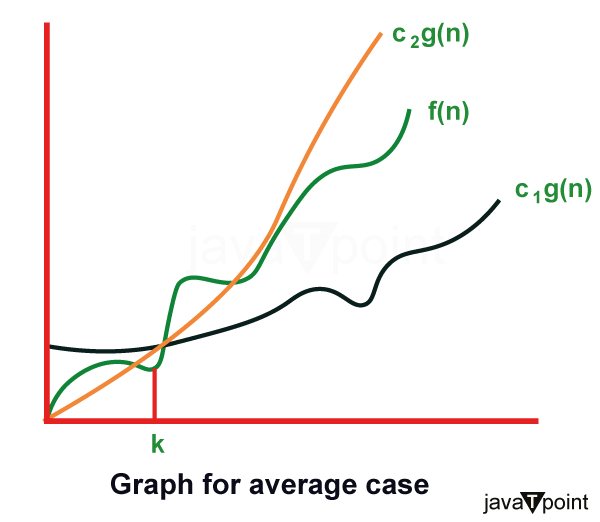
For Example:
3n+2= θ (n) as 3n+2≥3n and 3n+2≤ 4n, for n
k1=3,k2=4, and n0=2
Hence, the complexity of f (n) can be represented as θ (g(n)). The Theta Notation is more precise than both the big-oh and Omega notation. The function f (n) = θ (g (n)) if g(n) is both an upper and lower bound.
Next TopicAnalyzing Algorithm Control Structure
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










