Johnson's Algorithm

The problem is to find the shortest path between every pair of vertices in a given weighted directed graph and weight may be negative. Using Johnson's Algorithm, we can find all pairs shortest path in O (V² log ? V+VE ) time. Johnson's Algorithm uses both Dijkstra's Algorithm and Bellman-Ford Algorithm.

Johnson's Algorithm uses the technique of "reweighting." If all edge weights w in a graph G = (V, E) are nonnegative, we can find the shortest paths between all pairs of vertices by running Dijkstra's Algorithm once from each vertex. If G has negative - weight edges, we compute a new - set of non - negative edge weights that allows us to use the same method. The new set of edges weight w must satisfy two essential properties:

1. For all pair of vertices u, v ∈ V, the shortest path from u to v using weight function w is also the shortest path from u to v using weight function w.
2. For all edges (u, v), the new weight w (u, v) is nonnegative.

Given a weighted, directed graph G = (V, E) with weight function w: E→R and let h: v→R be any function mapping vertices to a real number.

For each edge (u, v) ∈ E define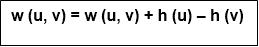

Where h (u) = label of u
h (v) = label of v

JOHNSON (G)
 1. Compute G' where V [G'] = V[G] ∪ {S} and
E [G'] = E [G] ∪ {(s, v): v ∈ V [G] }

 2. If BELLMAN-FORD (G',w, s) = FALSE
    then "input graph contains a negative weight cycle"
  else
    for each vertex v ∈ V [G']
     do h (v) ← δ(s, v)
  Computed by Bellman-Ford algorithm
 for each edge (u, v) ∈ E[G']
   do w (u, v) ← w (u, v) + h (u) - h (v)
 for each edge u ∈ V [G]
 do run DIJKSTRA (G, w, u) to compute
    δ (u, v) for all v ∈ V [G]
  for each vertex v ∈ V [G]
 do duv← δ (u, v) + h (v) - h (u)
Return D.

Example: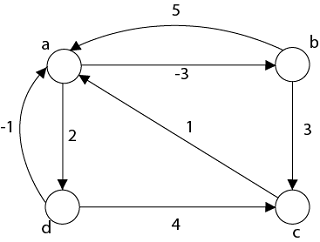

Step1: Take any source vertex's' outside the graph and make distance from's' to every vertex '0'.

Step2: Apply Bellman-Ford Algorithm and calculate minimum weight on each vertex.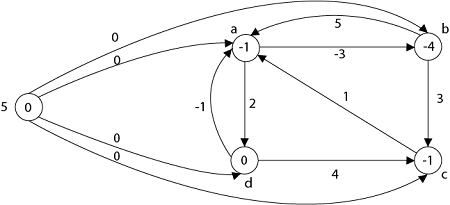

Step3: w (a, b) = w (a, b) + h (a) - h (b)
                        = -3 + (-1) - (-4)
                        = 0

w (b, a) = w (b, a) + h (b) - h (a)
              = 5 + (-4) - (-1)
              = 2
w (b, c) = w (b, c) + h (b) - h (c)
w (b, c) = 3 + (-4) - (-1)
             = 0
w (c, a) = w (c, a) + h (c) - h (a)
w (c, a) = 1 + (-1) - (-1)
             = 1
w (d, c) = w (d, c) + h (d) - h (c)
w (d, c) = 4 + 0 - (-1)
             = 5
w (d, a) = w (d, a) + h (d) - h (a)
w (d, a) = -1 + 0 - (-1)
             = 0
w (a, d) = w (a, d) + h (a) - h (d)
w (a, d) = 2 + (-1) - 0 = 1

Step 4: Now all edge weights are positive and now we can apply Dijkstra's Algorithm on each vertex and make a matrix corresponds to each vertex in a graph

Case 1: 'a' as a source vertex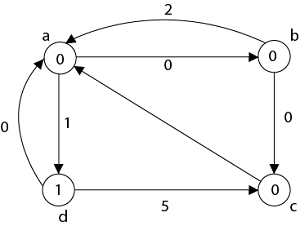

Case 2: 'b' as a source vertex

Case 3: 'c' as a source vertex

Case4:'d' as source vertex

Step5: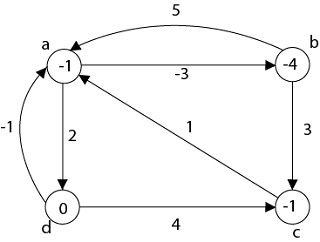

d_uv ← δ (u, v) + h (v) - h (u)
d (a, a) = 0 + (-1) - (-1) = 0
d (a, b) = 0 + (-4) - (-1) = -3
d (a, c) = 0 + (-1) - (-1) = 0
d (a, d) = 1 + (0) - (-1) = 2
d (b, a) = 1 + (-1) - (-4) = 4
d (b, b) = 0 + (-4) - (-4) = 0
d (c, a) = 1 + (-1) - (-1) = 1
d (c, b) = 1 + (-4) - (-1) = -2
d (c, c) = 0
d (c, d) = 2 + (0) - (-1) = 3
d (d, a) = 0 + (-1) - (0) = -1
d (d, b) = 0 + (-4) - (0) = -4
d (d, c) = 0 + (-1) - (0) = -1
d (d, d) = 0