Floyd-Warshall Algorithm

The Floyd-Warshall algorithm is a dynamic programming algorithm used to discover the shortest paths in a weighted graph, which includes negative weight cycles. The algorithm works with the aid of computing the shortest direction between every pair of vertices within the graph, the usage of a matrix of intermediate vertices to keep music of the exceptional-recognized route thus far.

But before we get started, let us briefly understand what Dynamic Programming is.

Understanding Dynamic Programming

Dynamic programming is a technique used in computer science and mathematics to remedy complicated troubles with the aid of breaking them down into smaller subproblems and solving each subproblem as simple as soon as. It is a technique of optimization that can be used to locate the pleasant technique to a hassle with the aid of utilizing the solutions to its subproblems.

The key idea behind dynamic programming is to keep the solutions to the subproblems in memory, so they can be reused later whilst solving larger problems. This reduces the time and area complexity of the set of rules and lets it resolve tons larger and extra complex issues than a brute force approach might.

There are two important styles of dynamic programming:

Memoization
Tabulation

Memoization involves storing the outcomes of every subproblem in a cache, in order that they may be reused later. Tabulation includes building a desk of answers to subproblems in a bottom-up manner, beginning with the smallest subproblems and working as much as the larger ones. Dynamic programming is utilized in an extensive range of packages, including optimization troubles, computational geometry, gadget studying, and natural language processing.

Some well-known examples of problems that may be solved by the usage of dynamic programming consist of the Fibonacci collection, the Knapsack trouble, and the shortest path problem.

History of Floyd-Warshall algorithm:

The Floyd-Warshall set of rules was advanced independently via Robert Floyd and Stephen Warshall in 1962. Robert Floyd turned into a mathematician and computer scientist at IBM's Thomas J. Watson Research Center, whilst Stephen Warshall became a computer scientist at the University of California, Berkeley. The algorithm was originally developed for use inside the field of operations research, where it turned into used to solve the all-pairs shortest direction problem in directed graphs with tremendous or negative side weights. The problem become of outstanding hobby in operations research, as it has many applications in transportation, conversation, and logistics.

Floyd first presented the set of rules in a technical record titled "Algorithm 97: Shortest Path" in 1962. Warshall independently discovered the set of rules quickly afterwards and posted it in his personal technical document, "A Theorem on Boolean Matrices". The algorithm has on account that emerged as a cornerstone of pc technology and is broadly used in lots of regions of studies and enterprise. Its capability to correctly find the shortest paths between all pairs of vertices in a graph, including those with terrible side weights, makes it a treasured tool for solving an extensive range of optimization problems.

Working of Floyd-Warshall Algorithm:

The set of rules works as follows:

Initialize a distance matrix D wherein D[i][j] represents the shortest distance between vertex i and vertex j.
Set the diagonal entries of the matrix to 0, and all other entries to infinity.
For every area (u,v) inside the graph, replace the gap matrix to mirror the weight of the brink: D[u][v] = weight(u,v).
For every vertex okay in the graph, bear in mind all pairs of vertices (i,j) and check if the path from i to j through k is shorter than the current best path. If it is, update the gap matrix: D[i][j] = min(D[i][j], D[i][k] D[k][j]).
After all iterations, the matrix D will contain the shortest course distances between all pairs of vertices.

Example:

Floyd-Warshall is an algorithm used to locate the shortest course between all pairs of vertices in a weighted graph. It works by means of keeping a matrix of distances between each pair of vertices and updating this matrix iteratively till the shortest paths are discovered.

Let's see at an example to illustrate how the Floyd-Warshall algorithm works:

Consider the following weighted graph: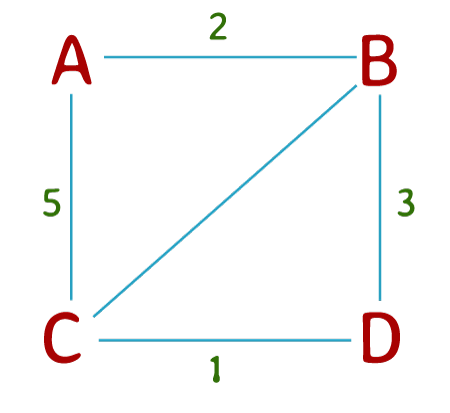

Figure: A Weighted Graph

In this graph, the vertices are represented by letters (A, B, C, D), and the numbers on the edges represent the weights of those edges.

To follow the Floyd-Warshall algorithm to this graph, we start by way of initializing a matrix of distances among every pair of vertices. If two vertices are immediately related by using a side, their distance is the load of that edge. If there may be no direct edge among vertices, their distance is infinite.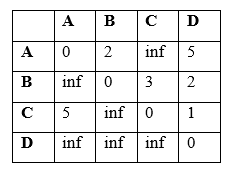

In the first iteration of the set of rules, we keep in mind the possibility of the usage of vertex 1 (A) as an intermediate vertex in paths among all pairs of vertices. If the space from vertex 1 to vertex 2 plus the space from vertex 2 to vertex three is much less than the present-day distance from vertex 1 to vertex three, then we replace the matrix with this new distance. We try this for each possible pair of vertices.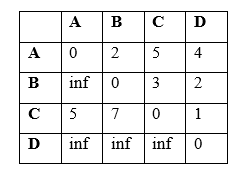

In the second iteration, we recollect the possibility to use of vertex 2 (B) as an intermediate vertex in paths among all pairs of vertices. We replace the matrix in the same manner as earlier before.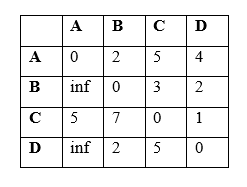

In the third iteration, we consider the possibility of using vertex 3 (C) as an intermediate vertex in paths between all pairs of vertices.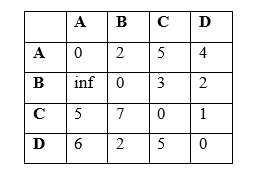

Finally, in the fourth and final iteration, we consider the possibility of using vertex 4 (D) as an intermediate vertex in paths between all pairs of vertices.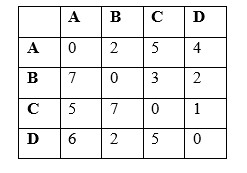

After the fourth iteration, we have got the shortest path between every pair of vertices in the graph. For example, the shortest path from vertex A to vertex D is 4, which is the value in the matrix at row A and column D.

Implementations of Floyd-Warshall Algorithm in Different Programming Languages:

We will now see the implementation of Floyd-Warshall Algorithm in different programming languages like C, C++, Java, and Python.

Code Implementation in C:

The following is the program code written in C for the implementation of Floyd-Warshall Algorithm.

Program Code:

#include <stdio.h>
#define INF 2147483647
 
int n = 4; // size of the adjaceny matrix
 
// O(n^2)
void fillDistanceMatrix(int A[n][n], int D[n][n]) {
   for (int i = 0; i < n; i++) {
       for (int j = 0; j < n; j++) {
           if (i == j)
               D[i][j] = 0;
           else if (A[i][j] == 0)
               D[i][j] = INF;
           else
               D[i][j] = A[i][j];
       }
   }
}
 
// O(n^3)
void floydWarshall(int A[n][n], int D[n][n]) {
   fillDistanceMatrix(A, D);
 
   for (int k = 0; k < n; k++) {
       for (int i = 0; i < n; i++) {
           for (int j = 0; j < n; j++) {
               if (D[i][k] < INF && D[k][j] < INF)
                   if (D[i][k] + D[k][j] < D[i][j])
                       D[i][j] = D[i][k] + D[k][j];
           }
       }
   }
}
int main() {
    int A[4][4] = {{0, 5, INF, 10},
                   {INF, 0, 3, INF},
                   {INF, INF, 0, 1},
                   {INF, INF, INF, 0}};
    int D[4][4];
 
    floydWarshall(A, D);
 
    printf("Shortest distances between all pairs of vertices:\n");
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            if (D[i][j] == INF)
                printf("%7s", "INF");
            else
                printf("%7d", D[i][j]);
        }
        printf("\n");
    }
 
    return 0;
}

Output:

Shortest distances between all pairs of vertices:
      0      5      8      9
    INF      0      3      4
    INF    INF      0      1
    INF    INF    INF      0

Code Implementation in C++:

The following is the program code written in C++ for the implementation of Floyd-Warshall Algorithm.

Program Code:

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
 
#define INF INT_MAX
 
// O(n^2)
vector<vector<int>> createDistanceMatrix(vector<vector<int>> A, int n) {
   vector<vector<int>> D(n, vector<int> (n, 0));
   for (int i = 0; i < n; i++) {
       for (int j = 0; j < n; j++) {
           if (i == j)
               D[i][j] = 0;
           else if (A[i][j] == 0)
               D[i][j] = INF;
           else
               D[i][j] = A[i][j];
       }
   }
   return D;
}
 
// O(n^3)
vector<vector<int>> floydWarshall(vector<vector<int>> A) {
   int n = A.size();
   vector<vector<int>> D = createDistanceMatrix(A, n);
 
   for (int k = 0; k < n; k++) {
       for (int i = 0; i < n; i++) {
           for (int j = 0; j < n; j++) {
               if (D[i][k] < INF && D[k][j] < INF)
                   D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
           }
       }
   }
 
   return D;
}
int main() {
    // Example graph
    vector<vector<int>> A = {{0, 5, INF, 10},
                             {INF, 0, 3, INF},
                             {INF, INF, 0, 1},
                             {INF, INF, INF, 0}};
 
    // Find shortest paths using Floyd-Warshall algorithm
    vector<vector<int>> D = floydWarshall(A);
 
    // Print the resulting distance matrix
    cout << "Shortest distances between all pairs of vertices:" << endl;
    for (int i = 0; i < D.size(); i++) {
        for (int j = 0; j < D.size(); j++) {
            if (D[i][j] == INF)
                cout << setw(5) << "INF";
            else
                cout << setw(5) << D[i][j];
        }
        cout << endl;
    }
 
    return 0;
}

Output:

Shortest distances between all pairs of vertices:
    0    5    8    9
  INF    0    3    4
  INF  INF    0    1
  INF  INF  INF    0

Code Implementation in Java:

The following is the program code written in Java for the implementation of Floyd-Warshall Algorithm.

Program Code:

class FloydWarshall {
   final static int INF = Integer.MAX_VALUE;
 
   public void FloydWarshall() {
 
   }
  
   // O(n^3)
   int[][] floydWarshall(int A[][]) {
       int n = A.length;
       int D[][] = createDistanceMatrix(A, n);
 
       for (int k = 0; k < n; k++) {
           for (int i = 0; i < n; i++) {
               for (int j = 0; j < n; j++) {
                   if (D[i][k] < INF && D[k][j] < INF)
                       D[i][j] = Math.min(D[i][j], D[i][k] + D[k][j]);
               }
           }
       }
  
       return D;
   }
 
   // O(n^2)
   int[][] createDistanceMatrix(int A[][], int n) {
       int D[][] = new int[n][n];
 
       for (int i = 0; i < n; i++) {
           for (int j = 0; j < n; j++) {
               if (i == j)
                   D[i][j] = 0;
               else if (A[i][j] == 0)
                   D[i][j] = INF;
               else
                   D[i][j] = A[i][j];
           }
       }
       return D;
   }
public static void main(String[] args) {
    FloydWarshall fw = new FloydWarshall();
    int[][] adjMatrix = {
        {0, 3, INF, 5},
        {2, 0, INF, 4},
        {INF, 1, 0, INF},
        {INF, INF, 2, 0}
    };
    int[][] shortestPaths = fw.floydWarshall(adjMatrix);
    for (int i = 0; i < shortestPaths.length; i++) {
        for (int j = 0; j < shortestPaths.length; j++) {
            System.out.printf("%d ", shortestPaths[i][j]);
        }
        System.out.println();
    }
}
}

Output:

Code Implementation in Python:

The following is the program code written in Python for the implementation of Floyd-Warshall Algorithm.

Program Code:

INF = float('inf')

# O(n^2)
def create_distance_matrix(A):
    n = len(A)
    D = [[0 if i == j else INF if A[i][j] == 0 else A[i][j] for j in range(n)] for i in range(n)]
    return D

# O(n^3)
def floyd_warshall(A):
    n = len(A)
    D = create_distance_matrix(A)

    for k in range(n):
        for i in range(n):
            for j in range(n):
                if D[i][k] < INF and D[k][j] < INF:
                    D[i][j] = min(D[i][j], D[i][k] + D[k][j])

    return D
adj_matrix = [
    [0, 3, 0, 5],
    [2, 0, 0, 4],
    [0, 1, 0, 0],
    [0, 0, 2, 0]
]
shortest_paths = floyd_warshall(adj_matrix)
for row in shortest_paths:
    print(row)

Output:

[0, 3, 6, 5]
[2, 0, 4, 4]
[inf, 1, 0, inf]
[inf, 4, 2, 0]

Understanding Time and Space Complexities of Floyd-Warshall Algorithm:

     Time complexity - O(n^3)
      Space complexity - O(n^2)

Time complexity - This algorithm has an overall time complexity of O(N^3), in which N is the wide variety of vertices within the graph. It is suitable for dense graphs with poor weight cycles, as it can manage them without getting caught in a limitless loop. However, for sparse graphs, different algorithms like Dijkstra's algorithm or Bellman-Ford algorithms can be extra efficient.

Let's complete our unfinished discussion of why the Bellman-Ford or Dijkstra's shortest path algorithm is not a suitable option for solving the shortest path problem including all pairs of nodes while we are talking about time complexity.

The Bellman-Ford and Dijkstra's shortest path algorithms only calculate the shortest path from one node to all other nodes, and their upper bounds, where nn and mm are the numbers of nodes and edges, respectively, are O(nm) and O(n+mlogn).

Additionally, Dijkstra's shortest path algorithm is ineffective for negative weighted edges.

If the Bellman-Ford algorithm is expanded to include all nodes, the time complexity changes to n*O(nm) = O(n^2*m).

The Floyd Warshall algorithm only considers the number of nodes, hence the maximum number of edges for a directed network can be as high as n*(n-1), meaning that the overall complexity could be as high as O(n^4).

As a result, the Floyd-Warshall algorithm is a better option!

Space Complexity - The algorithm requires a two-dimensional array, normally called a "distance matrix" to store the shortest path distances among every pair of vertices in the graph. The size of the space matrix is decided by way of the variety of vertices inside the graph, and it has a space complexity of O(V^2), wherein V is the range of vertices within the graph.

In addition to the space matrix, the algorithm additionally calls for a two-dimensional array to hold track of the intermediate vertices on the shortest path among any two vertices. This array is normally known as the "path matrix"; and it also has a space complexity of O(V^2).

Therefore, the general space complexity of the Floyd-Warshall set of rules is O(V^2), which means that the quantity of memory required through the algorithm grows quadratically with the variety of vertices inside the graph. This can be a problem for big graphs with many vertices, because the algorithm can fast turn out to be memory-extensive and won't be viable to run on machines with restricted memory.

Some Advantages and Disadvantages of Floyd-Warshall Algorithm:

Let us now discuss some advantages and disadvantages of using Floyd-Warshall Algorithm:

Advantages of the Floyd-Warshall algorithm include:

It can discover the shortest direction between all pairs of vertices in a weighted graph, such as graphs with negative edge weights.
It is an easy and smooth-to-put algorithm, making it accessible to developers of all skill ranges.
It is appropriate for both dense and sparse graphs.
It has a time complexity of O(N^3), that is relatively efficient for most real-international applications.
It can be used to discover negative weight cycles in a graph.

Disadvantages of the Floyd-Warshall set of rules include:

It calls for a matrix of size N^2 to store the intermediate results, which may be prohibitively large for extremely large graphs.
It is not the maximum green set of rules for fixing the all-pairs shortest path hassle in sure types of graphs, inclusive of sparse graphs or graphs with non-bad part weights.
It won't be suitable for real-time packages or packages with strict reminiscence constraints, as it is able to take a long term to compute the shortest paths in very huge graphs.
It can be less intuitive than different algorithms, which include Dijkstra's algorithm, or the Bellman-Ford set of rules, making it more difficult to understand for some builders.

Applications of Floyd Warshall Algorithm:

The Floyd-Warshall algorithm is a dynamic programming algorithm used for finding the shortest course among all pairs of vertices in a weighted graph. Here are some of the programs of the Floyd-Warshall algorithm:

Routing Algorithms: The Floyd-Warshall algorithm is broadly utilized in routing algorithms, along with within the OSPF (Open Shortest Path First) protocol utilized in Internet routing. It can help decide the shortest route among two nodes in a network and is useful in locating the least congested path.
Airline Networks: The Floyd-Warshall set of rules can also be utilized in airline networks to locate the shortest path between two cities with the lowest cost. It can assist airways plan their routes and limit fuel charges.
Traffic Networks: The algorithm is used to find the shortest path between points in a visitors' network. It can help reduce congestion and improve the go with the flow of visitors in city areas.
Computer Networks: The Floyd-Warshall algorithm is likewise utilized in laptop networks to decide the shortest course between hosts in a network. It can assist in minimizing community latency and improve community overall performance.
Game Development: The set of rules may be used in game development to find the shortest direction among two items in a sport world. It is beneficial in games in which the participant desires to navigate through complex surroundings, together with a maze or a metropolis.

These are only some of the numerous applications of the Floyd-Warshall algorithm. It is a powerful algorithm that can be applied in an extensive variety of fields to remedy a whole lot of troubles.

Next TopicCharacteristics of an Algorithm

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

Javatpoint Services

JavaTpoint offers too many high quality services. Mail us on h[email protected], to get more information about given services.

Website Designing
Website Development
Java Development
PHP Development
WordPress
Graphic Designing
Logo
Digital Marketing
On Page and Off Page SEO
PPC
Content Development
Corporate Training
Classroom and Online Training
Data Entry

Training For College Campus

JavaTpoint offers college campus training on Core Java, Advance Java, .Net, Android, Hadoop, PHP, Web Technology and Python. Please mail your requirement at [email protected].
Duration: 1 week to 2 week

^{Like/Subscribe us for latest updates or newsletter}

DAA Tutorial

Asymptotic Analysis

Recurrence

Analysis of Sorting

Divide and Conquer

Sorting

Lower bound Theory

Sorting in Linear Time

Hashing

Binary Search Trees

Red Black Tree

Dynamic Programming

Greedy Algorithm

Backtracking

MST

Shortest Path

All-Pairs Shortest Paths

Maximum Flow

Sorting Networks

Complexity Theory

Approximation Algo

String Matching

Misc

Interview Questions

Floyd-Warshall Algorithm

Understanding Dynamic Programming

History of Floyd-Warshall algorithm:

Working of Floyd-Warshall Algorithm:

Example:

Implementations of Floyd-Warshall Algorithm in Different Programming Languages:

Code Implementation in C:

Code Implementation in C++:

Code Implementation in Java:

Code Implementation in Python:

Understanding Time and Space Complexities of Floyd-Warshall Algorithm:

Some Advantages and Disadvantages of Floyd-Warshall Algorithm:

Advantages of the Floyd-Warshall algorithm include:

Disadvantages of the Floyd-Warshall set of rules include:

Applications of Floyd Warshall Algorithm:

Feedback

Help Others, Please Share

Learn Latest Tutorials

Preparation

Trending Technologies

B.Tech / MCA

Javatpoint Services

Training For College Campus