Minimum Spanning Tree

Before knowing about the minimum spanning tree, we should know about the spanning tree.

To understand the concept of spanning tree, consider the below graph: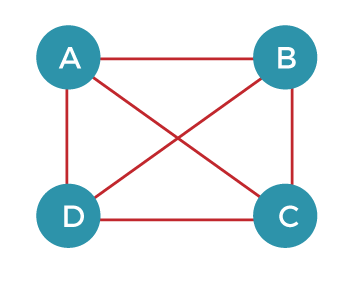

The above graph can be represented as G(V, E), where 'V' is the number of vertices, and 'E' is the number of edges. The spanning tree of the above graph would be represented as G`(V`, E`). In this case, V` = V means that the number of vertices in the spanning tree would be the same as the number of vertices in the graph, but the number of edges would be different. The number of edges in the spanning tree is the subset of the number of edges in the original graph. Therefore, the number of edges can be written as:

E` € E

It can also be written as:

E` = |V| - 1

Two conditions exist in the spanning tree, which is as follows:

• The number of vertices in the spanning tree would be the same as the number of vertices in the original graph.
  V` = V
• The number of edges in the spanning tree would be equal to the number of edges minus 1.
  E` = |V| - 1
• The spanning tree should not contain any cycle.
• The spanning tree should not be disconnected.

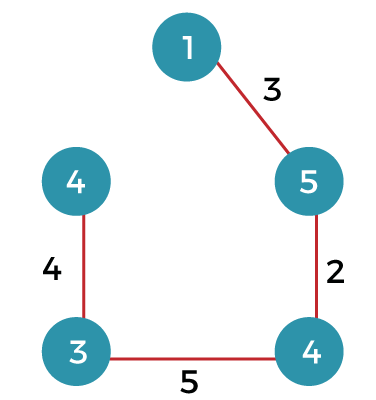
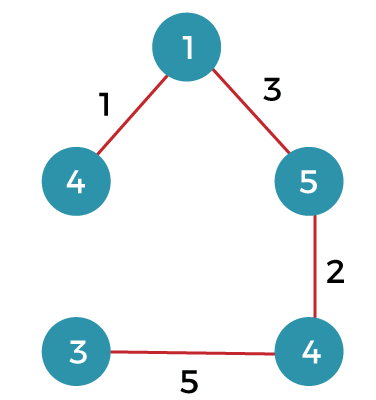
Note: A graph can have more than one spanning tree.

Consider the below graph:

The above graph contains 5 vertices. As we know, the vertices in the spanning tree would be the same as the graph; therefore, V` is equal 5. The number of edges in the spanning tree would be equal to (5 - 1), i.e., 4. The following are the possible spanning trees: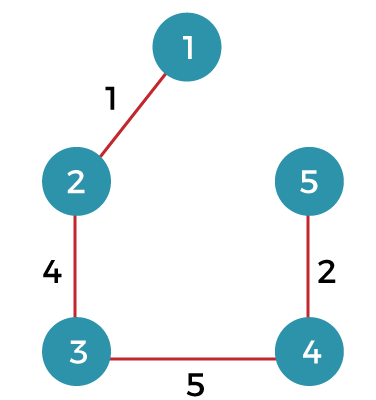

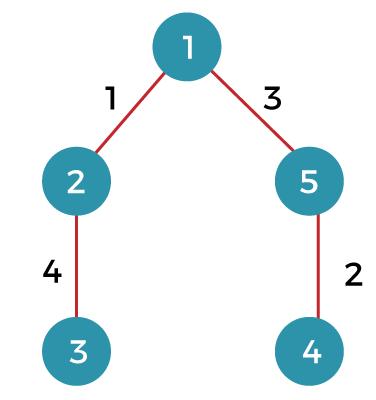
What is a minimum spanning tree?

The minimum spanning tree is a spanning tree whose sum of the edges is minimum. Consider the below graph that contains the edge weight:

The following are the spanning trees that we can make from the above graph.

• The first spanning tree is a tree in which we have removed the edge between the vertices 1 and 5 shown as below:
  The sum of the edges of the above tree is (1 + 4 + 5 + 2): 12
• The second spanning tree is a tree in which we have removed the edge between the vertices 1 and 2 shown as below:
  The sum of the edges of the above tree is (3 + 2 + 5 + 4) : 14
• The third spanning tree is a tree in which we have removed the edge between the vertices 2 and 3 shown as below:
  The sum of the edges of the above tree is (1 + 3 + 2 + 5) : 11
• The fourth spanning tree is a tree in which we have removed the edge between the vertices 3 and 4 shown as below:
  The sum of the edges of the above tree is (1 + 3 + 2 + 4) : 10. The edge cost 10 is minimum so it is a minimum spanning tree.

General properties of minimum spanning tree:

• If we remove any edge from the spanning tree, then it becomes disconnected. Therefore, we cannot remove any edge from the spanning tree.
• If we add an edge to the spanning tree then it creates a loop. Therefore, we cannot add any edge to the spanning tree.
• In a graph, each edge has a distinct weight, then there exists only a single and unique minimum spanning tree. If the edge weight is not distinct, then there can be more than one minimum spanning tree.
• A complete undirected graph can have an n^n-2 number of spanning trees.
• Every connected and undirected graph contains atleast one spanning tree.
• The disconnected graph does not have any spanning tree.
• In a complete graph, we can remove maximum (e-n+1) edges to construct a spanning tree.

Let's understand the last property through an example.

Consider the complete graph which is given below: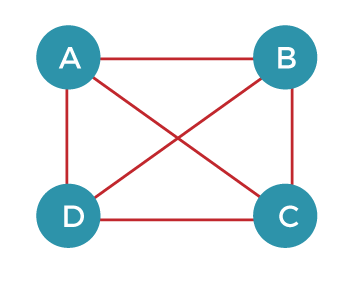

The number of spanning trees that can be made from the above complete graph equals to n^n-2 = 4^4-2 = 16.

Therefore, 16 spanning trees can be created from the above graph.

The maximum number of edges that can be removed to construct a spanning tree equals to e-n+1 = 6 - 4 + 1 = 3.