String Matching with Finite AutomataThe string-matching automaton is a very useful tool which is used in string matching algorithm. It examines every character in the text exactly once and reports all the valid shifts in O (n) time. The goal of string matching is to find the location of specific text pattern within the larger body of text (a sentence, a paragraph, a book, etc.) Finite Automata:A finite automaton M is a 5-tuple (Q, q0,A,∑δ), where
The finite automaton starts in state q0 and reads the characters of its input string one at a time. If the automaton is in state q and reads input character a, it moves from state q to state δ (q, a). Whenever its current state q is a member of A, the machine M has accepted the string read so far. An input that is not allowed is rejected. A finite automaton M induces a function ∅ called the called the final-state function, from ∑* to Q such that ∅(w) is the state M ends up in after scanning the string w. Thus, M accepts a string w if and only if ∅(w) ∈ A. The function f is defined as ∅ (∈)=q0 ∅ (wa) = δ ((∅ (w), a) for w ∈ ∑*,a∈ ∑) FINITE- AUTOMATON-MATCHER (T,δ, m), 1. n ← length [T] 2. q ← 0 3. for i ← 1 to n 4. do q ← δ (q, T[i]) 5. If q =m 6. then s←i-m 7. print "Pattern occurs with shift s" s The primary loop structure of FINITE- AUTOMATON-MATCHER implies that its running time on a text string of length n is O (n). Computing the Transition Function: The following procedure computes the transition function δ from given pattern P [1......m] COMPUTE-TRANSITION-FUNCTION (P, ∑) 1. m ← length [P] 2. for q ← 0 to m 3. do for each character a ∈ ∑* 4. do k ← min (m+1, q+2) 5. repeat k←k-1 6. Until 7. δ(q,a)←k 8. Return δ Example: Suppose a finite automaton which accepts even number of a's where ∑ = {a, b, c} 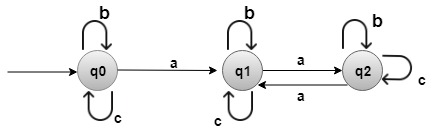
Solution: q0 is the initial state. 
Next TopicKnuth-Morris-Pratt Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









