Recurrence RelationA recurrence is an equation or inequality that describes a function in terms of its values on smaller inputs. To solve a Recurrence Relation means to obtain a function defined on the natural numbers that satisfy the recurrence. For Example, the Worst Case Running Time T(n) of the MERGE SORT Procedures is described by the recurrence. T (n) = θ (1) if n=1 2T There are four methods for solving Recurrence: 1. Substitution Method:The Substitution Method Consists of two main steps:
For Example1 Solve the equation by Substitution Method. T (n) = T We have to show that it is asymptotically bound by O (log n). Solution: For T (n) = O (log n) We have to show that for some constant c Put this in given Recurrence Equation. T (n) ≤c log Example2 Consider the Recurrence T (n) = 2T Find an Asymptotic bound on T. Solution: We guess the solution is O (n (logn)).Thus for constant 'c'. T (n) ≤c n logn Put this in given Recurrence Equation. Now, T (n) ≤2c 2. Iteration MethodsIt means to expand the recurrence and express it as a summation of terms of n and initial condition. Example1: Consider the Recurrence Solution:
T (n) = 2T (n-1)
= 2[2T (n-2)] = 22T (n-2)
= 4[2T (n-3)] = 23T (n-3)
= 8[2T (n-4)] = 24T (n-4) (Eq.1)
Repeat the procedure for i times
T (n) = 2i T (n-i)
Put n-i=1 or i= n-1 in (Eq.1)
T (n) = 2n-1 T (1)
= 2n-1 .1 {T (1) =1 .....given}
= 2n-1
Example2: Consider the Recurrence Solution:
T (n) = T (n-1) +1
= (T (n-2) +1) +1 = (T (n-3) +1) +1+1
= T (n-4) +4 = T (n-5) +1+4
= T (n-5) +5= T (n-k) + k
Where k = n-1
T (n-k) = T (1) = θ (1)
T (n) = θ (1) + (n-1) = 1+n-1=n= θ (n).
Next TopicRecursion Tree Method
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





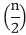 + θ (n) if n>1
+ θ (n) if n>1





