Complexity of AlgorithmThe term algorithm complexity measures how many steps are required by the algorithm to solve the given problem. It evaluates the order of count of operations executed by an algorithm as a function of input data size. To assess the complexity, the order (approximation) of the count of operation is always considered instead of counting the exact steps. O(f) notation represents the complexity of an algorithm, which is also termed as an Asymptotic notation or "Big O" notation. Here the f corresponds to the function whose size is the same as that of the input data. The complexity of the asymptotic computation O(f) determines in which order the resources such as CPU time, memory, etc. are consumed by the algorithm that is articulated as a function of the size of the input data. The complexity can be found in any form such as constant, logarithmic, linear, n*log(n), quadratic, cubic, exponential, etc. It is nothing but the order of constant, logarithmic, linear and so on, the number of steps encountered for the completion of a particular algorithm. To make it even more precise, we often call the complexity of an algorithm as "running time". Typical Complexities of an Algorithm
Since the constants do not hold a significant effect on the order of count of operation, so it is better to ignore them. Thus, to consider an algorithm to be linear and equally efficient, it must undergo N, N/2 or 3*N count of operation, respectively, on the same number of elements to solve a particular problem. How to approximate the time taken by the Algorithm?So, to find it out, we shall first understand the types of the algorithm we have. There are two types of algorithms:
However, it is worth noting that any program that is written in iteration could be written as recursion. Likewise, a recursive program can be converted to iteration, making both of these algorithms equivalent to each other. But to analyze the iterative program, we have to count the number of times the loop is going to execute, whereas in the recursive program, we use recursive equations, i.e., we write a function of F(n) in terms of F(n/2). Suppose the program is neither iterative nor recursive. In that case, it can be concluded that there is no dependency of the running time on the input data size, i.e., whatever is the input size, the running time is going to be a constant value. Thus, for such programs, the complexity will be O(1). For Iterative ProgramsConsider the following programs that are written in simple English and does not correspond to any syntax. Example1: In the first example, we have an integer i and a for loop running from i equals 1 to n. Now the question arises, how many times does the name get printed? Since i equals 1 to n, so the above program will print Edward, n number of times. Thus, the complexity will be O(n). Example2: In this case, firstly, the outer loop will run n times, such that for each time, the inner loop will also run n times. Thus, the time complexity will be O(n2). Example3: As we can see from the above example, we have two variables; i, S and then we have while S<=n, which means S will start at 1, and the entire loop will stop whenever S value reaches a point where S becomes greater than n. Here i is incrementing in steps of one, and S will increment by the value of i, i.e., the increment in i is linear. However, the increment in S depends on the i. Initially; i=1, S=1 After 1st iteration; i=2, S=3 After 2nd iteration; i=3, S=6 After 3rd iteration; i=4, S=10 … and so on. Since we don't know the value of n, so let's suppose it to be k. Now, if we notice the value of S in the above case is increasing; for i=1, S=1; i=2, S=3; i=3, S=6; i=4, S=10; … Thus, it is nothing but a series of the sum of first n natural numbers, i.e., by the time i reaches k, the value of S will be k(k+1)/2. To stop the loop, For Recursive ProgramConsider the following recursive programs. Example1: Solution; Here we will see the simple Back Substitution method to solve the above problem. T(n) = 1 + T(n-1) …Eqn. (1) Step1: Substitute n-1 at the place of n in Eqn. (1) T(n-1) = 1 + T(n-2) ...Eqn. (2) Step2: Substitute n-2 at the place of n in Eqn. (1) T(n-2) = 1 + T(n-3) …Eqn. (3) Step3: Substitute Eqn. (2) in Eqn. (1) T(n)= 1 + 1+ T(n-2) = 2 + T(n-2) …Eqn. (4) Step4: Substitute eqn. (3) in Eqn. (4) T(n) = 2 + 1 + T(n-3) = 3 + T(n-3) = …... = k + T(n-k) …Eqn. (5) Now, according to Eqn. (1), i.e. T(n) = 1 + T(n-1), the algorithm will run until n>1. Basically, n will start from a very large number, and it will decrease gradually. So, when T(n) = 1, the algorithm eventually stops, and such a terminating condition is called anchor condition, base condition or stopping condition. Thus, for k = n-1, the T(n) will become. Step5: Substitute k = n-1 in eqn. (5) T(n) = (n-1) + T(n-(n-1)) = (n-1) + T(1) = n-1+1 Hence, T(n) = n or O(n).
Next TopicAlgorithm Design Techniques
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




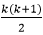 has to be greater than n, and when we solve this equation, we will get
has to be greater than n, and when we solve this equation, we will get 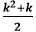 > n. Hence, it can be concluded that we get a complexity of O(√
> n. Hence, it can be concluded that we get a complexity of O(√




