Negative Weight Edges

It is a weighted graph in which the total weight of an edge is negative. If a graph has a negative edge, then it produces a chain. After executing the chain if the output is negative then it will give - ∞ weight and condition get discarded. If weight is less than negative and - ∞ then we can't have the shortest path in it.

Briefly, if the output is -ve, then both condition get discarded.

1. - ∞
2. Not less than 0.

And we cannot have the shortest Path.

Example: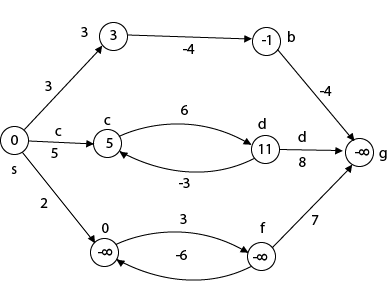

Suppose we want to calculate a path from s→c. So We have 2 paths /weight

Suppose we want to calculate a path from s→e. So we have two paths again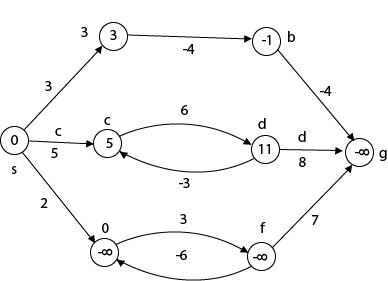

This figure illustrates the effects of negative weights and negative weight cycle on the shortest path weights.

Because there is only one path from "s to a" (the path <s, a>), δ (s, a) = w (s, a) = 3.

Furthermore, there is only one path from "s to b", so δ (s, b) = w (s, a) + w (a, b) = 3 + (-4) = - 1.

There are infinite many path from "s to c" : <s, c> : <s, c, d, c>, <s, c, d, c, d, c> and so on. Because the cycle <c, d, c> has weight δ (c, d) = w (c, d) + w (d, c) = 6 + (-3) = 3, which is greater than 0, the shortest path from s to c is <s, c> with weight δ (s, c) = 5.

Similarly, the shortest path from "s to d" is <s, c, d> with weight δ (s, d) = w (s, c) + w (s, d) = 11.

Analogously, there are infinite many paths from s to e: <s, e>, <s, e, f, e>, <s, e, f, e, f, e> and so on. Since the cycle <e, f, e> has weight δ (e, f) = w (e, f) + w (f, e) = 3 + (-6) = -3. So - 3 < 0, however there is no shortest path from s to e. B8y traversing the negative weight cycle <e, f, e>. This means path from s to e has arbitrary large negative weights and so δ (s, e) = - ∞.

Similarly δ (s, f) = - ∞ because g is reachable from f, we can also find a path with arbitrary large negative weight from s to g and δ (s, g) = - ∞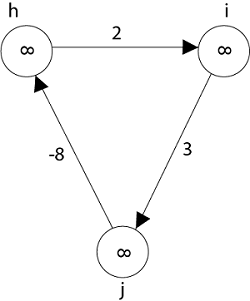

Vertices h, i, g also from negative weight cycle. They are also not reachable from the source node, so distance from the source is - ∞ to three of nodes (h, i, j).