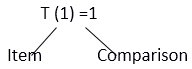Binary Search1. In Binary Search technique, we search an element in a sorted array by recursively dividing the interval in half. 2. Firstly, we take the whole array as an interval. 3. If the Pivot Element (the item to be searched) is less than the item in the middle of the interval, We discard the second half of the list and recursively repeat the process for the first half of the list by calculating the new middle and last element. 4. If the Pivot Element (the item to be searched) is greater than the item in the middle of the interval, we discard the first half of the list and work recursively on the second half by calculating the new beginning and middle element. 5. Repeatedly, check until the value is found or interval is empty. Analysis:
Case 1: item = A[mid], then LOC = mid, but it the best case and T (n) = 1 Case 2: item ≠A [mid], then we will split the array into two equal parts of size And again find the midpoint of the half-sorted array and compare with search element. Repeat the same process until a search element is found. T (n) = {Time to compare the search element with mid element, then with half of the selected half part of array}
At least there will be only one term left that's why that term will compare out, and only one comparison be done that's why Is the last term of the equation and it will be equal to 1
Next TopicMerge Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





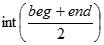
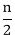 .
.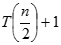 ...... (Equation 1)
...... (Equation 1)