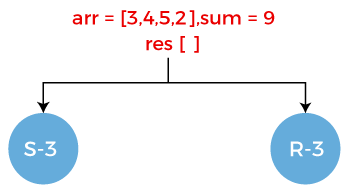Subset Sum Problem
It is one of the most important problems in complexity theory. The problem is given an A set of integers a1, a2,…., an upto n integers. The question arises that is there a non-empty subset such that the sum of the subset is given as M integer?. For example, the set is given as [5, 2, 1, 3, 9], and the sum of the subset is 9; the answer is YES as the sum of the subset [5, 3, 1] is equal to 9. This is an NP-complete problem again. It is the special case of knapsack
Let's understand this problem through an example.
problem.
We have a set of 5 integers given below:
N = 4, -2, 2, 3, 1
We want to find out the subset whose sum is equal to 5. There are many solutions to this problem.
The naïve approach, i.e., brute-force search generates all the possible subsets of the original array, i.e., there are 2n possible states. Here the running time complexity would be exponential. Then, we consider all these subsets in O(N) linear running time and checks whether the sum of the items is M or not.
The dynamic programming has pseudo-polynomial running time.
Statement: Given a set of positive integers, and a value sum, determine that the sum of the subset of a given set is equal to the given sum.
Or
Given an array of integers and a sum, the task is to have all subsets of given array with sum equal to the given sum.
There are two ways of solving the subset problem:
- Recursion
- Dynamic programming
Method 1: Recursion
Before knowing about the recursive approach, we should know about two things in a subset which are given below:
- Include: Here include means that we are selecting the element from the array.
- Exclude: Here, exclude means that we are rejecting the element from the array.
To implement the recursive approach, we consider the following two cases:
- Now we consider the first element and now the required sum is equal to the difference between the target sum and value of first element. The number of elements is equal to the difference between the total elements and 1.
- Leave the 'first' element and now the required sum = target sum. The number of elements is equal to the difference between the total elements and 1.
Let's understand that how can we solve the problem using recursion. Consider the array which is given below:
arr = [3, 4, 5, 2]
sum = 9
result = []
In the above example, we have taken an array, and the empty array named result that stores all the values whose resultant sum is equal to 9.
First element in an array is 3. There are two scenarios:
- First scenario is select. The sum is equal to the target sum - value of first element, i.e., 9 - 3 = 6 and the first element, i.e., 3 gets stored in the result array, i.e., result[].
- Second scenario is reject. The array arr contains the elements 4, 5, 2, i.e., arr = [4, 5, 2] and sum would be same as 9 as we are rejecting the element 3. The result[] array would remain empty.
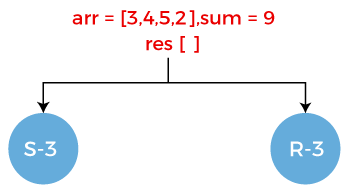
Now we perform the same select and reject operation on element 4 as it is the first element of the array now.
- Select the element 4 from the array. Since we are selecting 4 from the array so array arr would contain the elements 5, 2, i.e., arr = [5, 2]. The sum is equal to the 6-4 = 2 and the element 4 gets stored in the result arr. The result[] = {3, 4}.
- Reject the element 4 from the array. Since we are rejecting the 4 from the array so array arr would contain the elements 5, 2, i.e., arr = [5, 2]. The sum would remain same as 6 and the result array would be same as previous, i.e., {3}.
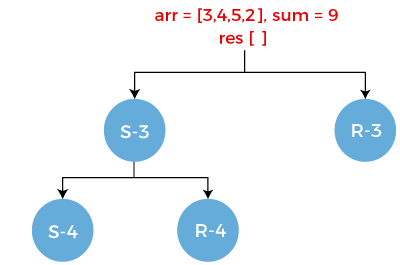
Now we perform the select and reject operation on element 5.
- Select the element 5 from the array. Since we are selecting 5 from the array so array arr would contain the elements 2, i.e., arr = [2]. The sum is equal to the 2 - 5 equals to -3 and the element 5 gets stored in the result arr. The result[] = {3, 4, 5}.
- Reject the element 5 from the array. Since we are rejecting 5 from the array so array arr would contain the element 2, i.e., arr = [2]. The sum would remain same as previous, i.e., 6 and the result array would be same as previous, i.e., {3, 4}.
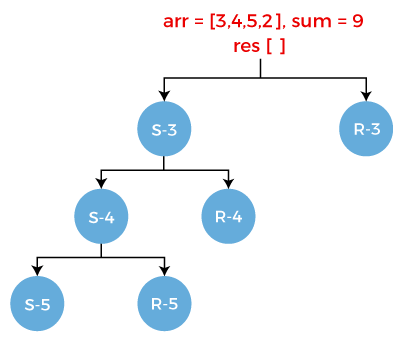
If we observe S-5, we can see that the sum is negative that returns false. It means that there is no further subset available in the set.
Consider R-5. It also has two scenarios:
- Select the element 2 from the array. Once the element 2 gets selected, the array becomes empty, i.e., arr[] = " ". The sum would be 2-2 equals to 0 and the element 2 gets stored in the result array. The result[] = [3, 4, 2].
- Reject the element 2 from the array. Once the element 2 gets rejected, the array becomes empty, i.e., arr[] = " ". The sum would be same as previous, i.e., 2 and the result array would also be same as previous, i.e., [3, 4].
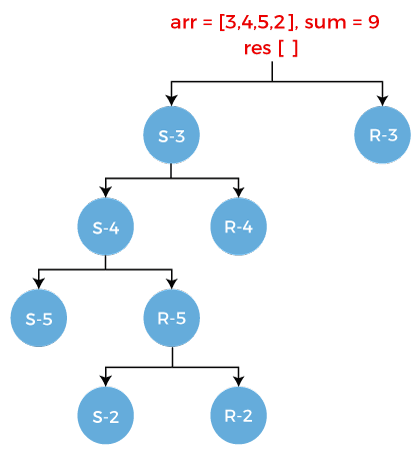
Consider R-4. It has two scenarios:
- Select the element 5 from the array. Since we are selecting 5 from the array so array arr would contain the elements 2, i.e., arr = [2]. The sum would be 6-5 equals to 1 and the element 5 gets stored in the result array. The result[] = [3, 5].
- Reject the element 5 from the array. Since we are rejecting 5 from the array so array arr would contain the element 2, i.e., arr = [2]. The sum would remain same as previous, i.e., 6 and the result array would be same as previous, i.e., {3}.
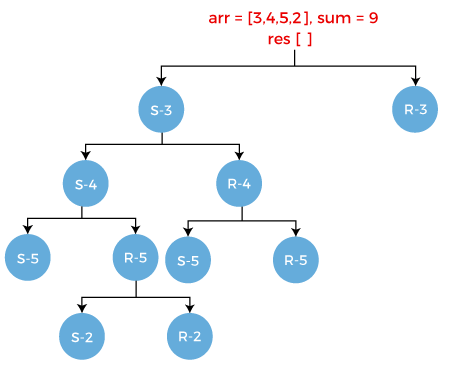
Consider S-5. It has two scenarios:
- Select the element 2 from the array. Since we are selecting 2 from the array so array arr would be empty, i.e., arr = " ". The sum would be 1-2 equals to -1 and the element 2 gets stored in the result array. The result[] = [3, 5, 2].
- Reject the element 2 from the array. Since we are rejecting 2 from the array so array arr would become empty. The sum would remain same as previous, i.e., 1 and the result array would be same as previous, i.e., {3, 5}.
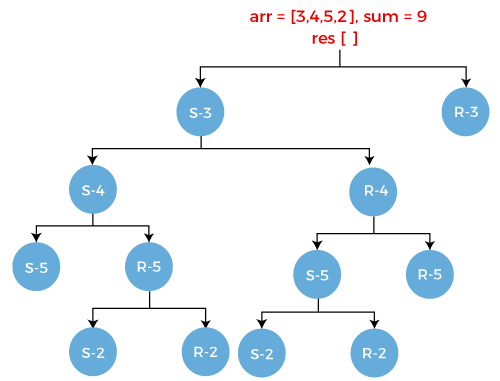
Consider R-5. It has two scenarios:
- Select the element 2 from the array. Since we are selecting 2 from the array so array arr would be empty, i.e., arr = " ". The sum would be 6-2 equals to 4 and the element 2 gets stored in the result array. The result[] = [3, 2].
- Reject the element 2 from the array. Since we are rejecting 2 from the array so array arr would become empty. The sum would remain same as previous, i.e., 6 and the result array would be same as previous, i.e., {3}.
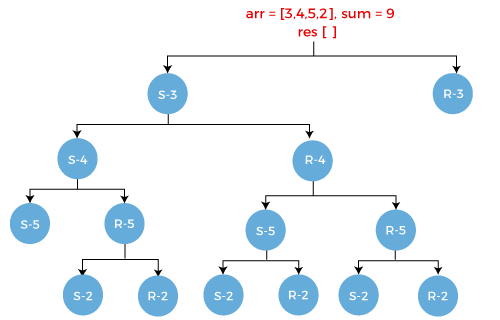
Similarly, we get the reject case, i.e., R-3 as shown as below:
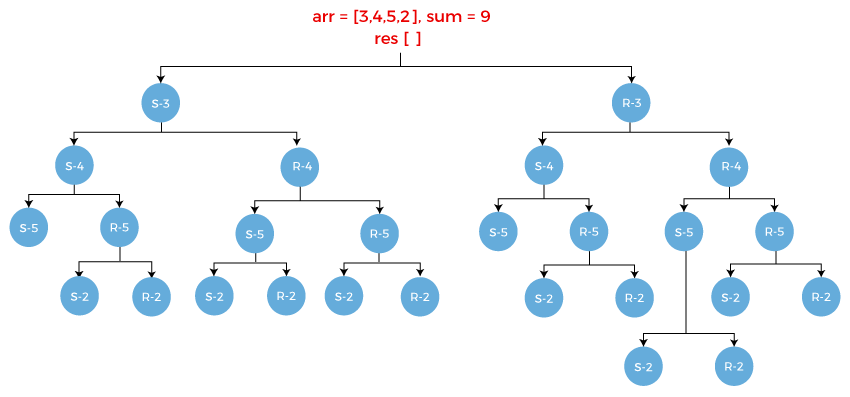
Following are the base conditions:
When we apply the base conditions on the above tree, then we will find two subsets given below:
S1 = {3, 4, 2}
S2 = {4, 5}
Implementation
Method 2: Dynamic Programming
Let A be an array or set which contains 'n' non-negative integers. Find a subset 'x' of set 'A' such that the sum of all the elements of x is equal to w where x is another input (sum).
For example:
A = {1, 2, 5, 9, 4}
Sum(w) = 18
Now we have to find out the subset from the given set whose sum is equal to 18. Here we will use the dynamic programming approach to solve the subset sum problem.
Example:
A = [2, 3, 5, 7, 10]
Sum(w) = 14
First, we create a table. The column contains the values from 0 to 14 while row contains the elements of the given set shown as below:
In the below table:
i: It represents the rows. Rows represents the elements.
j: It represents the columns. Columns represent the sum.
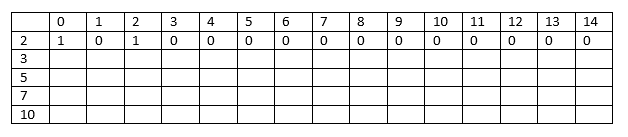
Consider the element 2. We will use 1 as a true value and 0 as a false value. The value 1 comes under 0 and 2 columns shown as below:
Here i=1, a[i] =2
Note: The rule for filling each column is given below:
Required sum = j - element
A[i][j] = A[i-1][required sum]
When j= 1
Required sum = 1 - 2 = -1; Since the sum is negative so put 0 under the column 1 as shown in the above table.
When j= 2
Required sum = 2 - 2 = 0; Since the value of sum is zero so we put 1 under the column 2 as shown in the above table.
We put 0 under the columns whose sum is greater than 2 as we cannot make sum more than 2 from the element 2.
Consider the element 3.
Here i = 2, a[i] = 3
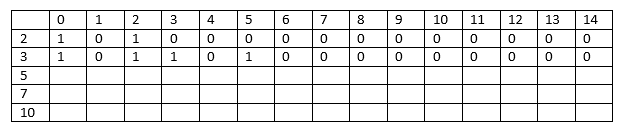
The columns whose sum is less than 3 will have the same values as the previous columns.
When j = 3, sum[j] = 3
Required sum = 3 -3 = 0; since the sum is zero so we put 1 under the column 3 as shown in the above table.
When j = 4; sum[j] = 4
Required sum = 4 - 3 = 1; Since the sum is 1 so we move to the previous row, i.e., i=1 and j=1. The value at a[1][1] is 0 so we put 0 at a[2][4].
When j = 5, sum[j] = 5
Required sum = 5 -3 = 2; The value of sum is 2 so the value at a[1][2] equals to 1. Therefore, the value at a[2][5] would be 1.
When j = 6, sum[j] = 6
Required sum = 6 -3 = 3; The value of sum is 3 so the value at a[1][3] equals to 0. Therefore, the value at a[2][6] would be 0.
When j = 7, sum[7] = 7
Required sum = 7 - 3 = 4; The value of sum is 4 so the value at a[1][4] equals to 0. Therefore, the value at a[2][7] would be 0.
In this way, we get the value 0 from the columns 8 to 14.
Consider the element 5.
Here i=3, a[i] = 5
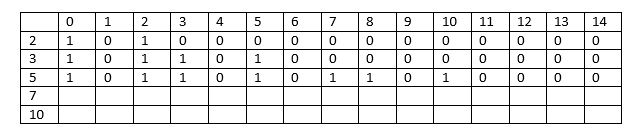
The columns whose sum is less than 5 will have the same values as the previous columns.
When j =5, sum[j] = 5
Required sum = 5-5 = 0; Since the value of sum is 0; therefore, the value at a[2][5] equals to 1.
When j = 6, sum[j] = 6
Required sum = 6-5 = 1; the value of sum is 1 so the value at a[2][1] equals to 0; therefore, the value at a[3][6] equals to 0.
When j=7, sum[j] = 7
Required sum = 7-5 = 2; the value of sum is 2 so the value at a[2][2] equals to 1; therefore, the value at a[3][7] equals to 1.
When j=8, sum[j] = 8
Required sum = 8-5 = 3; the value of sum is 3 so the value at a[2][3] equals to 1; therefore, the value at a[3][8] equals to 1.
When j=9, sum[j] =9
Required sum= 9-5 = 4; the value of sum is 4 so the value at a[2][4] equals to 0; therefore the value at a[3][9] equals to 0.
In this way, we get the values from the columns 10 to 14.
Consider the element 7.
Here i=4, a[i] =7
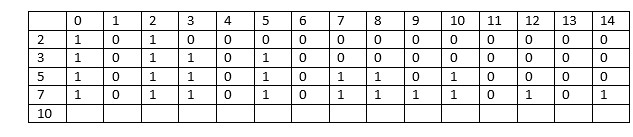
The columns whose sum is less than 7 will have the same values as the previous columns.
When j=9, sum[j] = 9
Required sum = 9 - 7 = 2; the value of sum is 2 so the value at a[3][2] equals to 1; therefore the value at a[4][9] equals to 1.
When j=10, sum[j] = 10
Required sum = 10 - 7= 3; the value of sum is 3 so the value at a[3][3] equals to 1; therefore, the value at a[4][10] equals to 1.
When j=11, sum[j] =11
Required sum = 11-7 = 4; the value of sum is 4 so the value at a[3][4] equals to 0; therefore, the value at a[4][11] equals to 0.
When j=12, sum[j] = 12
Required sum = 12-7 = 5; the value of sum is 5 so the value at a[3][5] equals to 1; therefore, the value at a[4][12] equals to 1.
When j=13, sum[j] =13
Required sum= 13 - 7 = 6; the value of sum is 6 so the value at a[3][6] equals to 0; therefore, the value at a[4][13] equals to 0.
When j=14, sum[j] = 14
Required sum = 14 - 7 = 7; the value of sum is 7 so the value at a[3][7] equals to 1; therefore, the value at a[4][14] equals to 1.
Consider the element 10
Here i=5, a[i] = 10
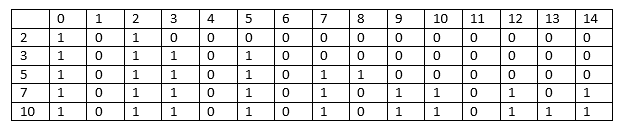
The columns whose sum is less than 10 will have the same values as the previous columns.
When j = 10, sum[j] = 10
Required sum = 10 - 10 = 0; the value of sum is 0 so the value at a[4][0] equals to 1; therefore, the value at a[5][10] equals to 1.
When j = 11, sum[j] = 11
Required sum = 11 - 10 = 1; the value of sum is 1 so the value at a[4][1] equals to 0; therefore, the value at a[5][11] equals to 0.
When j=12, sum[j] = 12
Required sum = 12-10 = 2; the value of sum is 2 so the value at a[4][2] equals to 1; therefore, the value at a[5][12] equals to 1.
When j=13, sum[j] = 13
Required sum = 13 - 10 = 3; the value of sum is 3 so the value at a[4][3] equals to 1; therefore, the value at a[5][13] equals to 1.
To determine whether the above given problem contains the subset or not, we need to check the last row and the last column. If the value is 1 which means that there would exist atleast one subset.
|







 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now