Single Source Shortest Path in a directed Acyclic Graphs

By relaxing the edges of a weighted DAG (Directed Acyclic Graph) G = (V, E) according to a topological sort of its vertices, we can figure out shortest paths from a single source in ∅(V+E) time. Shortest paths are always well described in a dag, since even if there are negative-weight edges, no negative-weight cycles can exist.

DAG - SHORTEST - PATHS (G, w, s)
 1. Topologically sort the vertices of G.
 2. INITIALIZE - SINGLE- SOURCE (G, s)
 3. for each vertex u taken in topologically sorted order
 4. do for each vertex v ∈ Adj [u]
 5. do RELAX (u, v, w) 

The running time of this data is determined by line 1 and by the for loop of lines 3 - 5. The topological sort can be implemented in ∅ (V + E) time. In the for loop of lines 3 - 5, as in Dijkstra's algorithm, there is one repetition per vertex. For each vertex, the edges that leave the vertex are each examined exactly once. Unlike Dijkstra's algorithm, we use only O (1) time per edge. The running time is thus ∅ (V + E), which is linear in the size of an adjacency list depiction of the graph.

Example: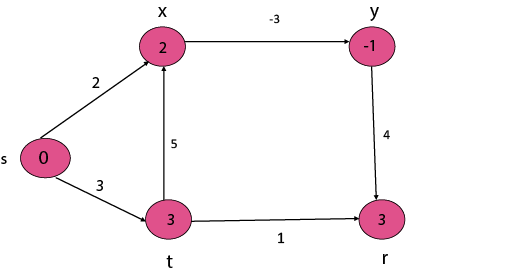

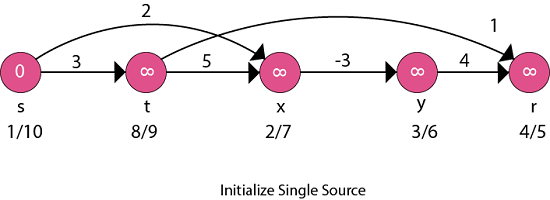
Step1: To topologically sort vertices apply DFS (Depth First Search) and then arrange vertices in linear order by decreasing order of finish time.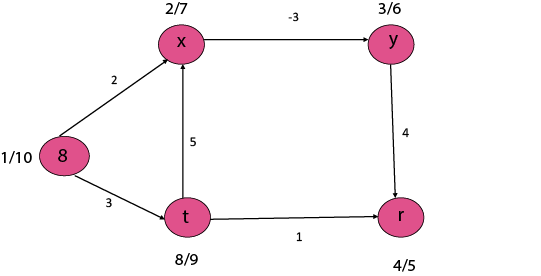

Now, take each vertex in topologically sorted order and relax each edge.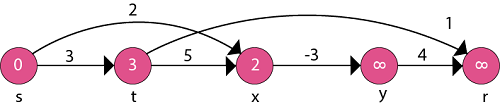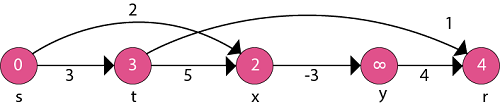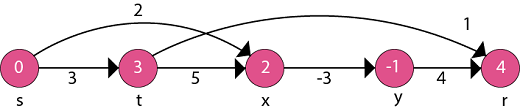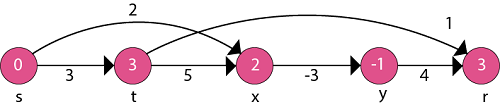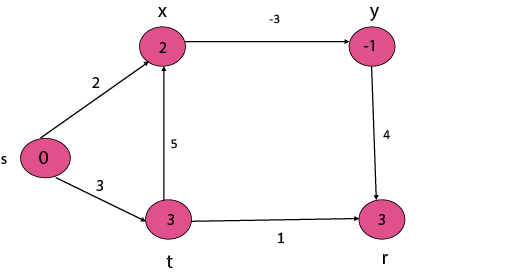

Thus the Shortest Path is: