CIRCUIT SATAccording to given decision-based NP problem, you can design the CIRCUIT and verify a given mentioned output also within the P time. The CIRCUIT is provided below:- 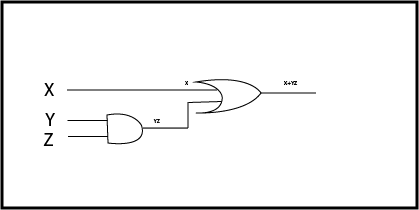
Note:- You can design a circuit and verified the mentioned output within Polynomial time but remember you can never predict the number of gates which produces the high output against the set of inputs/high inputs within a polynomial time. So you verified the production and conversion had been done within polynomial time. So you are in NPC.SAT (Satisfiability):-A Boolean function is said to be SAT if the output for the given value of the input is true/high/1 F=X+YZ (Created a Boolean function by CIRCUIT SAT) These points you have to be performed for NPC
Proof of NPC: - Reduction has been successfully made within the polynomial time from CIRCUIT SAT TO SAT. Output has also been verified within the polynomial time as you did in the above conversation. So concluded that SAT ϵ NPC.
Next Topic3-CNF Satisfiability
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










