Huffman Codes

• (i) Data can be encoded efficiently using Huffman Codes.
• (ii) It is a widely used and beneficial technique for compressing data.
• (iii) Huffman's greedy algorithm uses a table of the frequencies of occurrences of each character to build up an optimal way of representing each character as a binary string.

Suppose we have 10⁵ characters in a data file. Normal Storage: 8 bits per character (ASCII) - 8 x 10⁵ bits in a file. But we want to compress the file and save it compactly. Suppose only six characters appear in the file:

How can we represent the data in a Compact way?

(i) Fixed length Code: Each letter represented by an equal number of bits. With a fixed length code, at least 3 bits per character:

For example:

a			000

b			001

c			010

d			011

e			100

f			101

For a file with 10⁵ characters, we need 3 x 10⁵ bits.

(ii) A variable-length code: It can do considerably better than a fixed-length code, by giving many characters short code words and infrequent character long codewords.

For example:

  a       0

  b      101

  c      100

  d      111

  e      1101

  f      1100
Number of bits = (45 x 1 + 13 x 3 + 12 x 3 + 16 x 3 + 9 x 4 + 5 x 4) x 1000
= 2.24 x 105bits

Thus, 224,000 bits to represent the file, a saving of approximately 25%.This is an optimal character code for this file.

Prefix Codes:

The prefixes of an encoding of one character must not be equal to complete encoding of another character, e.g., 1100 and 11001 are not valid codes because 1100 is a prefix of some other code word is called prefix codes.

Prefix codes are desirable because they clarify encoding and decoding. Encoding is always simple for any binary character code; we concatenate the code words describing each character of the file. Decoding is also quite comfortable with a prefix code. Since no codeword is a prefix of any other, the codeword that starts with an encoded data is unambiguous.

Greedy Algorithm for constructing a Huffman Code:

Huffman invented a greedy algorithm that creates an optimal prefix code called a Huffman Code.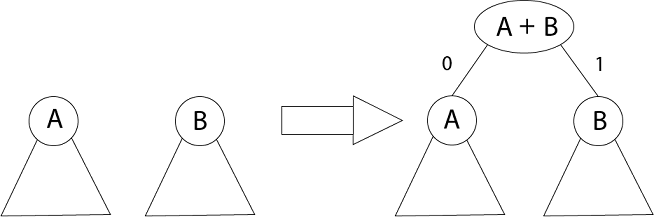

The algorithm builds the tree T analogous to the optimal code in a bottom-up manner. It starts with a set of |C| leaves (C is the number of characters) and performs |C| - 1 'merging' operations to create the final tree. In the Huffman algorithm 'n' denotes the quantity of a set of characters, z indicates the parent node, and x & y are the left & right child of z respectively.