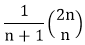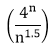Matrix Chain MultiplicationIt is a Method under Dynamic Programming in which previous output is taken as input for next. Here, Chain means one matrix's column is equal to the second matrix's row [always]. In general: If A = ⌊aij⌋ is a p x q matrix B = ⌊bij⌋ is a q x r matrix C = ⌊cij⌋ is a p x r matrix Then 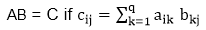
Given following matrices {A1,A2,A3,...An} and we have to perform the matrix multiplication, which can be accomplished by a series of matrix multiplications A1 xA2 x,A3 x.....x An Matrix Multiplication operation is associative in nature rather commutative. By this, we mean that we have to follow the above matrix order for multiplication but we are free to parenthesize the above multiplication depending upon our need. In general, for 1≤ i≤ p and 1≤ j ≤ r 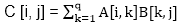
It can be observed that the total entries in matrix 'C' is 'pr' as the matrix is of dimension p x r Also each entry takes O (q) times to compute, thus the total time to compute all possible entries for the matrix 'C' which is a multiplication of 'A' and 'B' is proportional to the product of the dimension p q r. It is also noticed that we can save the number of operations by reordering the parenthesis. Example1: Let us have 3 matrices, A1,A2,A3 of order (10 x 100), (100 x 5) and (5 x 50) respectively. Three Matrices can be multiplied in two ways:
No of Scalar multiplication in Case 1 will be: No of Scalar multiplication in Case 2 will be: To find the best possible way to calculate the product, we could simply parenthesis the expression in every possible fashion and count each time how many scalar multiplication are required. Matrix Chain Multiplication Problem can be stated as "find the optimal parenthesization of a chain of matrices to be multiplied such that the number of scalar multiplication is minimized". Number of ways for parenthesizing the matrices: There are very large numbers of ways of parenthesizing these matrices. If there are n items, there are (n-1) ways in which the outer most pair of parenthesis can place. (A1) (A2,A3,A4,................An) Or (A1,A2) (A3,A4 .................An) Or (A1,A2,A3) (A4 ...............An) ........................ It can be observed that after splitting the kth matrices, we are left with two parenthesized sequence of matrices: one consist 'k' matrices and another consist 'n-k' matrices. Now there are 'L' ways of parenthesizing the left sublist and 'R' ways of parenthesizing the right sublist then the Total will be L.R: 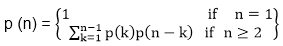
Also p (n) = c (n-1) where c (n) is the nth Catalon number c (n) = On applying Stirling's formula we have c (n) = Ω Which shows that 4n grows faster, as it is an exponential function, then n1.5. Development of Dynamic Programming Algorithm
Dynamic Programming ApproachLet Ai,j be the result of multiplying matrices i through j. It can be seen that the dimension of Ai,j is pi-1 x pj matrix. Dynamic Programming solution involves breaking up the problems into subproblems whose solution can be combined to solve the global problem. At the greatest level of parenthesization, we multiply two matrices A1.....n=A1....k x Ak+1....n) Thus we are left with two questions:
One possible answer to the first question for finding the best value of 'k' is to check all possible choices of 'k' and consider the best among them. But that it can be observed that checking all possibilities will lead to an exponential number of total possibilities. It can also be noticed that there exists only O (n2 ) different sequence of matrices, in this way do not reach the exponential growth. Step1: Structure of an optimal parenthesization: Our first step in the dynamic paradigm is to find the optimal substructure and then use it to construct an optimal solution to the problem from an optimal solution to subproblems. Let Ai....j where i≤ j denotes the matrix that results from evaluating the product Ai Ai+1....Aj. If i < j then any parenthesization of the product Ai Ai+1 ......Aj must split that the product between Ak and Ak+1 for some integer k in the range i ≤ k ≤ j. That is for some value of k, we first compute the matrices Ai.....k & Ak+1....j and then multiply them together to produce the final product Ai....j. The cost of computing Ai....k plus the cost of computing Ak+1....j plus the cost of multiplying them together is the cost of parenthesization. Step 2: A Recursive Solution: Let m [i, j] be the minimum number of scalar multiplication needed to compute the matrixAi....j. If i=j the chain consist of just one matrix Ai....i=Ai so no scalar multiplication are necessary to compute the product. Thus m [i, j] = 0 for i= 1, 2, 3....n. If i<j we assume that to optimally parenthesize the product we split it between Ak and Ak+1 where i≤ k ≤j. Then m [i,j] equals the minimum cost for computing the subproducts Ai....k and Ak+1....j+ cost of multiplying them together. We know Ai has dimension pi-1 x pi, so computing the product Ai....k and Ak+1....jtakes pi-1 pk pj scalar multiplication, we obtain m [i,j] = m [i, k] + m [k + 1, j] + pi-1 pk pj There are only (j-1) possible values for 'k' namely k = i, i+1.....j-1. Since the optimal parenthesization must use one of these values for 'k' we need only check them all to find the best. So the minimum cost of parenthesizing the product Ai Ai+1......Aj becomes 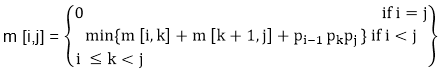
To construct an optimal solution, let us define s [i,j] to be the value of 'k' at which we can split the product Ai Ai+1 .....Aj To obtain an optimal parenthesization i.e. s [i, j] = k such that m [i,j] = m [i, k] + m [k + 1, j] + pi-1 pk pj
Next TopicMatrix Chain Multiplication Example
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share