Sliding Window Algorithm

You will undoubtedly encounter several algorithms if you study computer science. The sliding window algorithm is a technique that finds application in data transfer and computer networks, among other areas. It is utilized for flow control in the TCP (Transmission Control Protocol). In addition, this method may be used to construct a variety of competitive issues. Thus, it would be best to comprehend this algorithm to ace the interview with your desired employer. The sliding window algorithm and its implementation in three distinct programming languages are covered in this article.

A method for lowering algorithm complexity is the sliding window algorithm. It is employed in such a way that fewer loops are required, which optimizes the program. In this method, the outcome of the previous step is used to calculate the outcome of the following.

The window-sliding approach aims to replace nested loops with a single loop and minimize the number of time-consuming computations.

Scope

A description of the Sliding Window Algorithm and an example of its use are provided in this article. Steps to fix sliding window issues are also included in the post.

The Sliding Window method is illustrated multiple times in this article.

Sliding Window Algorithm: What is it?

Think about a lengthy chain that is connected. Consider applying oil to the entire chain with your hands rather than pouring it from above.

One method for doing this is to pick up some oil, apply it to a piece of the chain, pick up some more oil, apply it to the area after that where oil hasn't yet been applied, and so on until the entire chain is lubricated.

You may also achieve this by dipping a cloth in oil and using it to grasp the chain at one end. Instead of repeatedly redipping the material, slip it with one hand onto the next portion, then the next, until you reach the other end.

The second method is called the "Sliding Window Technique," and the part that slides from one end to the other is called the "Sliding Window."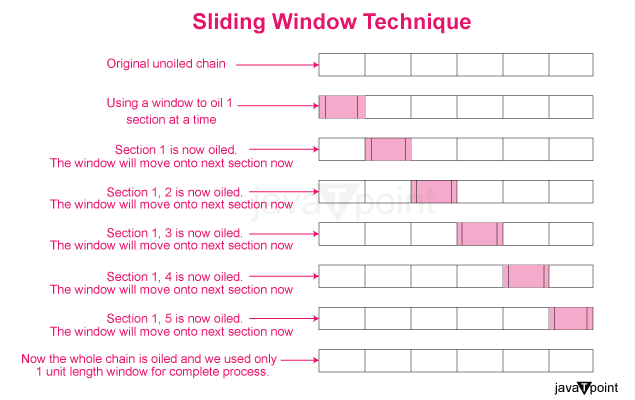

With this technique, we may quickly calculate items with a defined computation window and obtain the results more efficiently than the nested loops (naive approach). This algorithm's primary objective is to utilize the result from one window to calculate the result from the following window.

Let's say a group of 12 friends decides to hold a party together, but the main question is who will throw the treat. After much deliberation, they decided that since they were seated at a round table, the group of three people whose ages were the highest among groups of the same size would be responsible for paying the bill.

The naïve technique would be to consider each individual and loop over the following three people's ages to locate that group, but it would take O(12*3) units of time. The sliding window method allows us to shrink this issue from O(12*3) to O(12). We'll see how to utilize the sliding Window method to resolve this issue in the following section.

A requirement for using the sliding window method

In a unique situation, when the size of the computing window is fixed throughout the whole nested loop, it is possible to employ the sliding window approach. The temporal complexity may only be lowered after that.

Sliding Window Technique: How Do I Use It?

The following examples show how the sliding window approach is generally used:

Determine the necessary window size.
From the beginning of the data structure, compute the result for the first window.
Then, move the window by 1 using a loop and continue calculating the outcome window by window.

In the previously given example, we may apply the sliding window approach.

We'll start by adding the total ages of the three members, then we'll keep adding the next one and deducting the last one to obtain the total ages of the three people after each step, which we can then compare. Here, the window size is 3, and we move the window to compute the age sum of the following group. This is a complete sliding window algorithm with an O(12) unit time complexity. The section of this approach that slides each time is the sliding window, which may be used to solve most sliding window issues.

Let's say that the age range of the pupils is [21, 23, 24, 22, 21, 26, 23, 22, 21, 24, 20]

And the various windows of the three persons who are seated next to one another are [21,23,24], [23,24,22], [24,22,22], [22,22,21], [22,21,26], [21,26,23], [26,23,22], [23,22,21], [22,21,24], and [21,24,20].

Here, the sums are each calculated using the sliding window method; let's look at our strategy.

The first three add up to 21+23+24 = 68, the next three add up to 68-21+22 = 69, 69-23+22 = 68, and so on until the final one. The needed response may be discovered by comparing the amounts calculated at each stage.

Simple Solutions for Sliding Window Issues

The following are the steps for applying the sliding window technique:

Determine the window size inside which the algorithm must run.
Determine the first window's outcome as we would in a naïve method.
Keep the cursor in the starting location.
Next, execute a loop while advancing the window one step at a time and moving the cursor one at a time, and record the outcomes for each window.

Let's explore how these procedures may be used to fix sliding window issues. Consider the situation where we must determine the highest sum of m items in an array of integers arr with n elements.

Example:

If n = 5 and arr[5] = 10, 20, 10, 30, 5, the answer would be 60 (20 + 10 + 30).
If n = 7 and arr[7] = 2, 10, 17, 1, 9, 13, 4, and m = 4, the answer is 40 (17+1+9+13).

The simple solution to this problem is to execute a loop for each element, followed by another nested loop to compute the total of the following m items, retaining the maximum at each stage.

The Sliding Window Technique is used to develop an optimized approach:

How can we calculate the outcome using the sliding window method?

We compute the sum of the array's first m items and save the result in a variable called running_sum.
After that, we'll move the window, execute a loop linearly on the array until the end, and maintain track of the maximum_sum by comparing it to the running_sum each time.
We add the next element, remove the first element, and raise the first pointer as we obtain the total of m items for a window each time.
Every time, this will provide us with maximum_sum.

Issue Statement

Before continuing with the problem's method, let's first grasp it. Finding the most considerable sum of K consecutive elements, given an array of size N, is the problem's stated challenge. Need help understanding it? Fear not; we shall comprehend this by using an illustration.

Assume we are given the following array and told to discover the three consecutive integers that add up to the most fantastic sum. K in this situation thus equals 3.

arr = [16, 12, 9, 19, 11, 8]

The following blocks in the supplied array have three consecutive entries: [16, 12, 9], [12, 9, 19], [9, 19, 11], and [19, 11, 8]. Now that we have calculated the total of each block, it is as follows: 37, 40, 39, and 38. The highest total among all of these estimated amounts is forty. As a result, 40 is our output.

Naive strategy

There is a straightforward but ineffective solution to this issue. You might be asking why we're discussing this strategy if it needs to be more effective. One must understand the value of a sound strategy, right? Additionally, by comprehending this strategy, we may build on our expertise to create the sliding window method, a more effective algorithm.

With this method, we start with the first index and keep adding until we get to the kth element. We repeat the operation for all conceivable sets of k successive blocks or groups of k items. This method uses a nested for loop; the outer for loop starts with the first element in the k-element block and runs until it reaches the kth element.

Because this method uses two nested loops, its complexity is O(N*K). Where k is the number of consecutive subentries to be considered, and n is the size of the array provided to us. Can't trust it when we tell you that this work can be completed quickly? Check it out for yourself here.

Sliding Window Technique

Let's use an analogy to assist us in comprehending this strategy. Consider a pane fixed inside a window with length n and length k. Currently, the pane is 0 units, or far left, from the center. Combine the n-element array arr[] in the window with the k-element current sum in the pane. If we exert force on the window, it will advance a unit distance. The pane will cover the following k elements.

The last element of the current block is added, and the first element of the preceding block is subtracted to get the current total at each step. I'm done now! The entire sliding window algorithm looks like this. Easy, huh? Let's now examine this approach's algorithm.

Window Sliding Algorithm

The steps for using the sliding window algorithm are as follows:

Compute the sum of the first K elements and store it in the current variable. Save it in the variable maximum sum because it is the initial sum, hence the current maximum.
Given that the window size is K, we reposition the window to the right and compute the window's item total.
If the current exceeds the maximum sum, step 3 updates the maximum, and step 2 is repeated.

Example

Now that we have an example let's further grasp the method. The starting value of the maximum sum variable is 0, and the procedure is then started. In this instance, k is also assumed to be 3.

Finding the total of the first three consecutive integers, or the numbers from index 0 to 2, is where we start. This first window's sum, which is 37, is kept in the current variable. Since the current now exceeds the maximumSum, the maximumSum variable's value is modified to record 37.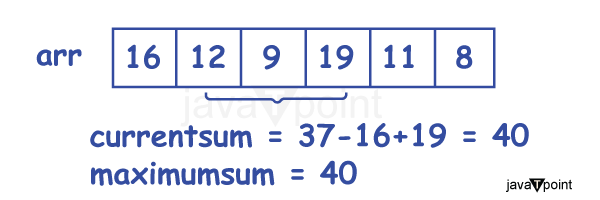

The following three digits are covered by sliding the window a unit distance. By taking 16 out of the current and adding 19 to it, the total of the new current window is calculated. 40 is the current value of the current. Since the most recent current value exceeds the maximumSum when compared, 40 will be stored in the maximumSum variable.

The next 3 digits are covered by shifting the window once more. When 12 is subtracted from the current sum and 11 is added, the result is 39, which is the sum for this window. Because this amount is smaller than maximumSum, maximumSum's value stays the same.

A new window now covers the last three numbers. At this point, the total is determined to equal 38. This variable's value is unaffected since it is lower than maximumSum's (40) value. Now that all three consecutive number combinations have been considered, their sums have all been determined. Finally, the maximum sum, represented by the number 40, is returned.

Sliding Window Algorithm in Python

def maxSum(arr, k):
	# length of the array
	n = len(arr)

	# length of the array must be greater
        # window size
	if n < k:
		print("Invalid")
		return -1

	# sum of first k elements
	window_sum = sum(arr[:k])
	max_sum = window_sum

	# remove the  first element of previous
	# window and add the last element of
	# The current window to calculate the 
    # The sum of remaining windows by
	for i in range(n - k):
		window_sum = window_sum - arr[i] + arr[i + k]
		max_sum = max(window_sum, max_sum)

	return max_sum


arr = [16, 12, 9, 19, 11, 8]
k = 3
print(maxSum(arr, k))

Output:

Sliding Window Algorithm in C++

#include 
using namespace std;

// Returns maximum sum in a subarray of size k.
int maxSum(int arr[], int n, int k) {
    // n must be greater
    if (n < k) {
        cout << "Invalid";
        return -1;
    }

    //sum of the first window of size k
    int window_sum = 0;
    for (int i = 0; i < k; i++)
        window_sum += arr[i];

    // Compute sums of remaining windows by
    // removing the first element of previous
    // window and adding the last element of
    // current window.
    int max_sum = window_sum;
    for (int i = k; i < n; i++) {
        window_sum += (arr[i] - arr[i - k]);
        max_sum = max(max_sum, window_sum);
    }
    return max_sum;
}

int main(){
    int n = 5 , k = 3;;
    int arr[] = { 16,12,9,19,11,8};
    cout << maxSum(arr, n, k);
    return 0;
}

Output:

Sliding Window Algorithm in Java

public class sliding window {

    static int maxSum(int[] arr,int k){
        //length of the array
        int n=arr.length;

        //length of array(n) must be greater than window size(k)
        if(n<k){
            System.out.println("Invalid");
            return -1;
        }

        //sum of first k(window size) elements
        int window_sum=0;
        for(int i=0;i<k;i++) window_sum+=arr[i];

        int max_sum=window_sum;

        //Calculating sums of remaining windows by
        //removing the first element of the previous window
        //and adding the last element of the current window
        //this way, our window moves forward.

        //Also updating the maximum sum to the current window sum
        //If the current window sum is greater
        // than the existing maximum sum.
        for(int i=k;i<n;i++){
            window_sum+=(arr[i]-arr[i-k]);
            max_sum=Math.max(window_sum,max_sum);
        }

        return max_sum;
    }

    public static void main(String[] args) {
        //window size
        int k=3;
        int[] arr={16, 12, 9, 19, 11, 8};
        System.out.println(maxSum(arr,k));
    }


}

Output:

Complicated timing

Given that we use a single loop to compute the most considerable sum in the technique mentioned earlier, the time complexity of the code is O(N).

Conclusion

For competitive coding, the sliding window algorithm is an important subject. Many issues may be resolved by making a few little adjustments to the algorithm. In this essay, we first recognize the issue statement before recognizing the simplistic solution. Finally, we learned a more effective method and its C++, Java, and Python source code. Our professionals are available around the clock to assist you with any code problems you could have.

The Sliding Window Algorithm is heavily utilized, with the window size used for any problem-solving or algorithm analysis remaining constant throughout the program. The naïve method may then be optimized using the Sliding Window Technique, and the complexity can be decreased.
This sliding window algorithm's time complexity, where N is the number of items present, is O(N).
It must always be used when the window's size is fixed.
Depending on our preferences and the task requirements, we may implement this algorithm in various ways, such as iterating from right to left or left to right.

Next TopicDifference Between Algorithms and Flowcharts

← prev next →