Traveling Salesperson problem using branch and boundGiven the vertices, the problem here is that we have to travel each vertex exactly once and reach back to the starting point. Consider the below graph: 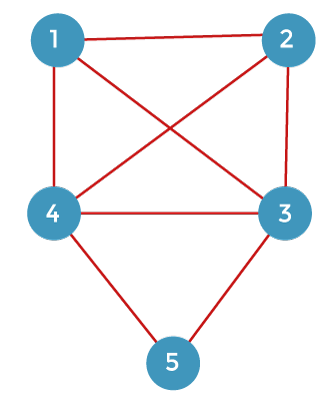
As we can observe in the above graph that there are 5 vertices given in the graph. We have to find the shortest path that goes through all the vertices once and returns back to the starting vertex. We mainly consider the starting vertex as 1, then traverse through the vertices 2, 3, 4, and 5, and finally return to vertex 1. The adjacent matrix of the problem is given below: 
Now we look at how this problem can be solved using the branch n bound. Let's first understand the approach then we solve the above problem. The graph is given below, which has four vertices: 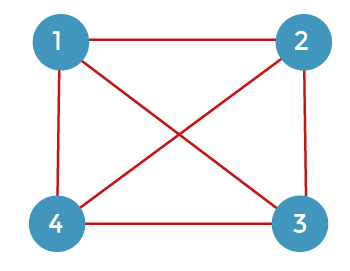
Suppose we start travelling from vertex 1 and return back to vertex 1. There are various ways to travel through all the vertices and returns to vertex 1. We require some tools that can be used to minimize the overall cost. To solve this problem, we make a state space tree. From the starting vertex 1, we can go to either vertices 2, 3, or 4, as shown in the below diagram. 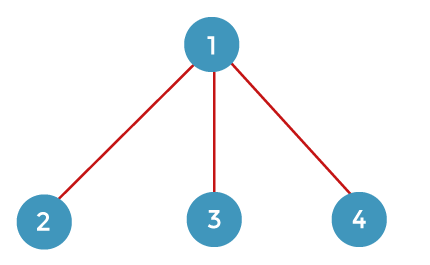
From vertex 2, we can go either to vertex 3 or 4. If we consider vertex 3, we move to the remaining vertex, i.e., 4. If we consider the vertex 4 shown in the below diagram: 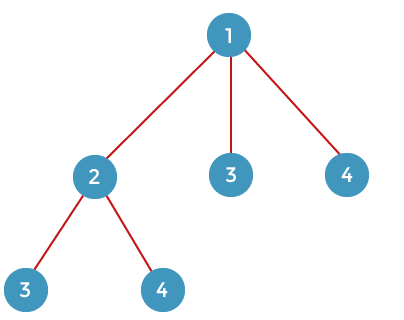
From vertex 3, we can go to the remaining vertices, i.e., 2 or 4. If we consider the vertex 2, then we move to remaining vertex 4, and if we consider the vertex 4 then we move to the remaining vertex, i.e., 3 shown in the below diagram: 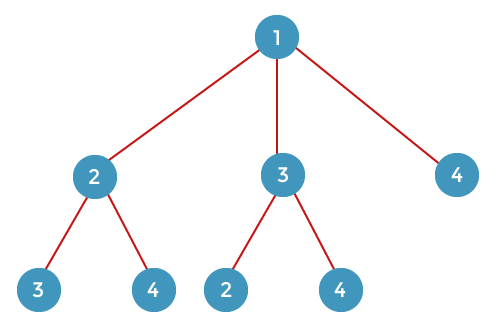
From vertex 4, we can go to the remaining vertices, i.e., 2 or 3. If we consider vertex 2, then we move to the remaining vertex, i.e., 3, and if we consider the vertex 3, then we move to the remaining vertex, i.e., 2 shown in the below diagram: 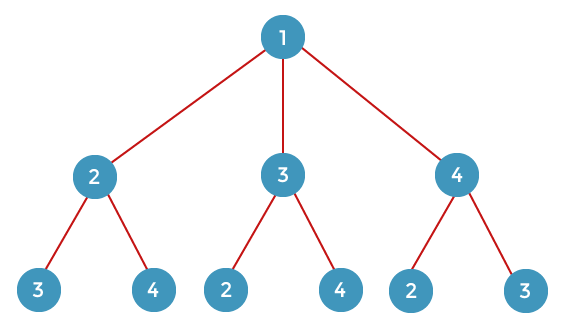
The above is the complete state space tree. The state space tree shows all the possibilities. Backtracking and branch n bound both use the state space tree, but their approach to solve the problem is different. Branch n bound is a better approach than backtracking as it is more efficient. In order to solve the problem using branch n bound, we use a level order. First, we will observe in which order, the nodes are generated. While creating the node, we will calculate the cost of the node simultaneously. If we find the cost of any node greater than the upper bound, we will remove that node. So, in this case, we will generate only useful nodes but not all the nodes. Let's consider the above problem. 

As we can observe in the above adjacent matrix that 10 is the minimum value in the first row, 2 is the minimum value in the second row, 2 is the minimum value in the third row, 3 is the minimum value in the third row, 3 is the minimum value in the fourth row, and 4 is the minimum value in the fifth row. Now, we will reduce the matrix. We will subtract the minimum value with all the elements of a row. First, we evaluate the first row. Let's assume two variables, i.e., i and j, where 'i' represents the rows, and 'j' represents the columns. When i = 0, j =0 M[0][0] = ∞-10= ∞ When i = 0, j = 1 M[0][1] = 20 - 10 = 10 When i = 0, j = 2 M[0][2] = 30 - 10 = 20 When i = 0, j = 3 M[0][3] = 10 - 10 = 0 When i = 0, j = 4 M[0][4] = 11 - 10 = 1 The matrix is shown below after the evaluation of the first row: 
Consider the second row. When i = 1, j =0 M[1][0] = 15-2= 13 When i = 1, j = 1 M[1][1] = ∞ - 2= ∞ When i = 1, j = 2 M[1][2] = 16 - 2 = 14 When i = 1, j = 3 M[1][3] = 4 - 2 = 2 When i = 1, j = 4 M[1][4] = 2 - 2 = 0 The matrix is shown below after the evaluation of the second row: 
Consider the third row: When i = 2, j =0 M[2][0] = 3-2= 1 When i = 2, j = 1 M[2][1] = 5 - 2= 3 When i = 2, j = 2 M[2][2] = ∞ - 2 = ∞ When i = 2, j = 3 M[2][3] = 2 - 2 = 0 When i = 2, j = 4 M[2][4] = 4 - 2 = 2 The matrix is shown below after the evaluation of the third row: Consider the fourth row: When i = 3, j =0 M[3][0] = 19-3= 16 When i = 3, j = 1 M[3][1] = 6 - 3= 3 When i = 3, j = 2 M[3][2] = 18 - 3 = 15 When i = 3, j = 3 M[3][3] = ∞ - 3 = ∞ When i = 3, j = 4 M[3][4] = 3 - 3 = 0 The matrix is shown below after the evaluation of the fourth row: 
Consider the fifth row: When i = 4, j =0 M[4][0] = 16-4= 12 When i = 4, j = 1 M[4][1] = 4 - 4= 0 When i = 4, j = 2 M[4][2] = 7 - 4 = 3 When i = 4, j = 3 M[4][3] = 16 - 4 = 12 When i = 4, j = 4 M[4][4] = ∞ - 4 = ∞ The matrix is shown below after the evaluation of the fifth row: 
The above matrix is the reduced matrix with respect to the rows. Now we reduce the matrix with respect to the columns. Before reducing the matrix, we first find the minimum value of all the columns. The minimum value of first column is 1, the minimum value of the second column is 0, the minimum value of the third column is 3, the minimum value of the fourth column is 0, and the minimum value of the fifth column is 0, as shown in the below matrix: Now we reduce the matrix. Consider the first column. When i = 0, j =0 M[0][0] = ∞-1= ∞ When i = 1, j = 0 M[1][0] = 13 - 1= 12 When i = 2, j = 0 M[2][0] = 1 - 1 = 0 When i = 3, j = 0 M[3][0] = 16 - 1 = 15 When i = 4, j = 0 M[4][0] = 12 - 1 = 11 The matrix is shown below after the evaluation of the first column: 
Since the minimum value of the first and the third columns is non-zero, we will evaluate only first and third columns. We have evaluated the first column. Now we will evaluate the third column. Consider the third column. When i = 0, j =2 M[0][2] = 20-3= 17 When i = 1, j = 2 M[1][2] = 13 - 1= 12 When i = 2, j = 2 M[2][2] = 1 - 1 = 0 When i = 3, j = 2 M[3][2] = 16 - 1 = 15 When i = 4, j = 2 M[4][2] = 12 - 1 = 11 The matrix is shown below after the evaluation of the third column: 
The above is the reduced matrix. The minimum value of rows is 21, and the columns is 4. Therefore, the total minimum value is (21 + 4) equals to 25. Let's understand that how to solve this problem using branch and bound with the help of a state-space tree. To make a state-space tree, first, we consider node 1. From node 1, we can go either to nodes 2, 3, 4, or 5 as shown in the below image. The cost of node 1 would be the cost which we achieved in the above-reduced matrix, i.e.., 25. Here, we will also maintain the upper bound. Initially, the upper bound would-be infinity. 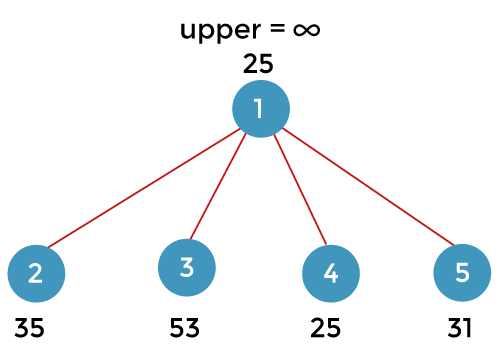
Now, consider node 2. It means that we are moving from node 1 to node 2. Make the first row and second column as infinity shown in the below matrix: Once we move from node 1 to node 2, we cannot move back to node 1. Therefore, we have to make 2 to 1 as infinity shown in the below matrix: 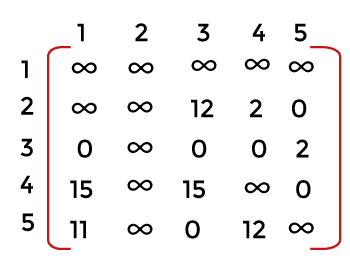
Since each row and column contains atleast one zero value; therefore, we can say that above matrix has been reduced. The cost of reduction of node 2 is c(1, 2) + r + r` = 10 + 25 + 0 = 35. Now we will find the minimum value of each column of the new reduced matrix. The minimum value of the first column is 11 and the minimum value of other three columns is 0. Now, consider the node 3. It means that we are moving from the node 1 to node 3. Make the first row and third column as infinity shown in the below matrix: 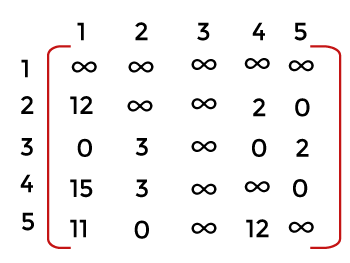
Once we move from the node 1 to node 3, we cannot move back to the node 1. Therefore, we have to make 3 to 1 as infinity shown in the below matrix: Since each row and column contains atleast one zero value; therefore, we can say that above matrix has been reduced. The cost of reduction of node 3 is c(1, 3) + r + r` = 17 + 25 + 11= 53. Now, consider the node 4. It means that we are moving from the node 1 to node 4. Make the first row and forth column as infinity shown in the below matrix: 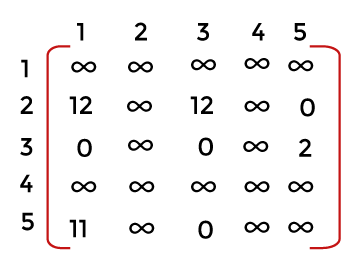
Once we move from the node 1 to node 4, we cannot move back to the node 1. Therefore, we have to make 4 to 1 as infinity shown in the below matrix: Since each row and column contains atleast one zero value; therefore, we can say that above matrix has been reduced. The cost of reduction of node 4 is c(1, 4) + r + r` = 0 + 25 + 0 = 25. Now, consider the node 5. It means that we are moving from the node 1 to node 5. Make the first row and fifth column as infinity shown in the below matrix: Once we move from the node 1 to node 5, we cannot move back to the node 1. Therefore, we have to make 5 to 1 as infinity shown in the below matrix: Since each row and column contains atleast one zero value; therefore, we can say that above matrix has been reduced. In this case, second and third rows are non-zero. Therefore, we have to first find the minimum values of both the rows. The minimum value of second row is 2; therefore, we subtract 2 from all the elements of the second row. The elements of second row would be: A[1][0] = 12-2 = 10 A[1][1] = ∞ A[1][2] = 11 - 2 = 9 A[1][3] = 2 - 2 = 0 A[1][4] = ∞ - 2 = ∞ As we can observe now that the second row contains one zero value. The cost of reduction of node 5 is c(1, 5) + r + r` = 1 + 25 + 5 = 31 Since the node 4 has the minimum cost, i.e., 25. So we will explore the node 4 first. From the vertex 4, we can go either to the vertex 2, 3 or 5 as shown in the below image: Now we have to calculate the cost of the path from the vertex 4 to 2, vertex 4 to 3, and vertex 4 to 5. Here, we will use the matrix of node 4 to find the cost of all the nodes. First, we consider the path from the vertex 4 to the vertex 2. We make fourth row as ∞ and second column as ∞. Since we cannot move back from 2 to 1, so 1 to 2 is also infinity as shown in the below matrix: Since all the rows and columns have atleast one zero value. Therefore, we can say that this matrix is already reduced. So, there would be no reduction cost. The cost of reduction of node 2 is c(4, 2) + r + r` = 3 + 25 + 0 = 28 Now we have to calculate the cost of the path from the vertex 4 to the vertex 3. We make fourth row and third column as infinity as shown in the below matrix. Since we cannot move from the vertex 3 to 1, so we make 3 to 1 as infinity shown in the below matrix: Now we will check whether each row and column contain atleast one zero value or not. First, we observe all the rows. Since the third row does not have a zero value, so we first find the minimum value of the third row. The minimum value of the third row is 2, so we subtract 2 from all the elements of the third row. The elements of third row would be: A[2][0] = ∞ - 2 = ∞ A[2][1] = 3 - 2 = 1 A[2][2] = ∞ - 2 = ∞ A[2][3] = ∞ - 2 = ∞ A[2][4] = 2 - 2 = 0 As we can observe now that the third row contains one zero value. The first column does not contain the zero value. The minimum value of the first column is 11. We subtract 11 from all the elements of the first column. The elements of first column would be: A[0][0] = ∞ - 11 = ∞ A[1][0] = 12 - 11 = 1 A[2][0] = ∞ - 11= ∞ A[3][0] = ∞ - 11= ∞ A[4][0] = 11 - 11 = 0 As we can observe now that the first column contains one zero value. The total minimum cost is 11 +2 equals to 13. The cost of reduction of node 3 is c(4, 3) + r + r` = 12 + 25 + 13 = 50. Now we will calculate the cost of the path from the vertex 4 to 5. We make fourth row and fifth column as infinity. Since we cannot move back from the node 5 to 1, so we also make 1 to 5 as infinity shown in the below matrix: Now we will check whether each row and column contain atleast one zero value or not. First, we observe all the rows. The second row does not contain the zero value, so we find the minimum value of the second row. The minimum value is 11 so we subtract 11 from all the elements of the second row. The elements of second row would be: A[1][0] = 12 - 11 = 1 A[1][1] = ∞ - 11 = ∞ A[1][2] = 11 - 11 = 0 A[1][3] = ∞ - 11 = ∞ A[1][4] = ∞ - 11 = ∞ As we can observe now that the second row contains one zero value. The cost of reduction of node 5 is c(4, 5) + r + r` = 0 + 25 + 11 = 36. Now we will compare the cost of all the leaf nodes. The node with a cost 28 is minimum so we will explore this node. The node with a cost 28 can be further expanded to the nodes 3 and 5 as shown in the below figure: Now we have to calculate the cost of both the nodes, i.e., 3 and 5. First we consider the path from node 2 to node 3. Consider the matrix of node 2 which is shown below: We make second row and third column as infinity. Also, we cannot move back from the node 3 to node 1 so we make 3 to 1 as infinity as shown in the below matrix: 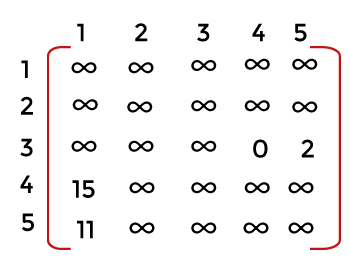
Now we will check whether any row contains zero value or not. Since third row does not contain any zero value so we will find the minimum value of the third row. The minimum value of the third row is 2 so we subtract 2 from all the elements of the third row. The elements of third row would be: A[2][0] = ∞ - 2 = ∞ A[2][1] = ∞ - 2 = ∞ A[2][2] = ∞ - 2 = ∞ A[2][3] = ∞ - 2 = ∞ A[2][4] = 2 - 2 = 0 Since fifth row does not contain any zero value so we will find the minimum value of the fifth row. The minimum value of the fifth row is 11 so we subtract 11 from all the elements of the fifth row. A[4][0] = 11 - 11 = 0 A[4][1] = ∞ - 11 = ∞ A[4][2] = ∞ - 11 = ∞ A[4][3] = ∞ - 11 = ∞ A[4][4] = ∞ - 11 = ∞ The total minimum cost is (11 + 2) equals to 13. The cost of reduction of node 3 is c(2, 3) + r + r` = 11 + 28 + 13 = 52. Consider the path from node 2 to node 5. Make the fourth row and third column as infinity. Since we cannot move back from the node 5 to node 1 so make 1 to 5 also as infinity as shown in the below matrix: Now we will check whether any row contains zero value or not. Since every row and column contains a zero value; therefore, the above matrix is the reduced matrix. The cost of reduction of node 5 is c(2, 5) + r + r` = 0 + 28 + 0 = 28 Now we will find out the leaf node with a minimum cost. The node 5 with a cost 28 is minimum so we select node 5 for the further exploration. The node 5 can be further expanded to the node 3 as shown in the below figure: Here, we will use the matrix of node 5 having cost 28 as shown below: Consider the path from node 5 to node 3. Make the fifth row and third column as infinity. Since we cannot move back from the node 3 to node 1 so make 1 to 5 also as infinity as shown in the below matrix: Now we will check whether any row contains zero value or not. Since every row and column contains a zero value; therefore, the above matrix is the reduced matrix. The cost of reduction of node 3 is c(5, 3) + r + r` = 0 + 28 + 0 = 28. Finally, we traverse all the nodes. The upper value is updated from infinity to 28. We will check whether any leaf node has a value less than 28. Since no leaf node contains the value less than 28 so we discard all the leaf nodes from the tree as shown below: The path of the tour would be 1->4->2->5->3.
Next Topic#
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










