Regular Expression Matching

Regular Expression Matching is also one of the classic dynamic programming problems.

Suppose a string S is given and a regular expression R, write a function to check whether a string S matches a regular expression R. Assume that S contains only letters and numbers.

A regular expression consists of:

• Letters A-Z
• Numbers 0-9
• '*': Matches 0 or more characters
• '.': Matches one character

Let's understand through an example.

Consider a string:

S = "ABBBAC"

Consider a regular expression as:

R = ".*A*"

Now we will compare the string with a regular expression given above.

In the Regular expression,

The first character is a '.' character. The '.' Character means that it should be with any one character. It is matched with 'A' character.

The second character is a '*' character. The '*' character means that it should be matched with either 0 or more characters, so it is matched with 3 'B' characters from the string.

The third character is a 'A'. The 'A' character with an 'A' from the string S.

The fourth character is a '*' character, and it is matched with an 'C' character from the string.

Therefore, all the characters of the regular expression are matched with a String S. It returns a true value.

Let's take another example.

Consider the below string.

S = "GREATS"

R = "G*T*E"

Now we have to compare string and regular expression R.

The first character 'G' in regular expression R is matched with the first character of string 'G'.

The second character in the regular expression '*' is matched with "REA" in the string.

The third character 'T' in the regular expression is matched 'T' in the string.

The fourth character '*' is matched with an 'S' character.

The fifth character, i.e., 'E' does not match with any character in the string.

Therefore, we can say that the regular expression does not match with a string which is given above, so it returns a False value.

Now let's see the step-by-step approach to solve this problem.

First, we will define the state of the system.

Parameters

We will use the two indices, i.e., i and j where,

i: It is the last index of the substring S.

j: It is the last index of the substring R.

Cost function

We will define a function matches(i, j, S, R); this function returns true if substring of S ending at i matches a substring of regular expression R ending at j.

Second, we define the Transitions.

The base case here is that i=-1, j=-1, return true which means that both S and R are empty and all the characters from the string S are matched with a regular expression R.

If i>=0 and j= -1, return false which means that some characters in S are unmatched with the characters in R. Here i>=0 means that the substring S is not empty whereas j= -1 means that the regular expression R is empty.

If i=0 and j>=0, return false which means that some characters in R are unmatched.

Let's see how this approach works.

S = ABBBAC

R = .*A*

Initially, 'i' points to the last character of the string S, i.e., C whereas the 'j' points to the last character of the regular expression, i.e., *.

First case: '*' matches with one character of S, i.e., 'C'. In this case, 'i' moves ahead and points to 'A' and 'j' would be at the same location pointing to the character '*'.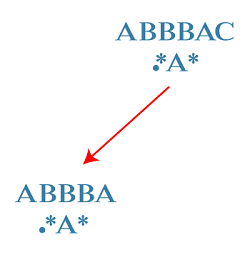

Second case: '*' matches with no character. In this case, 'i' would remain at the same location and 'j' moves ahead and points to A character.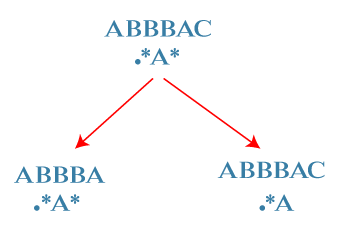

First, we will solve the left-subtree.

S = ABBBA

R = .*A*

Again, there are two cases:

Either '*' matches with 0 character or one character.

First case: '*' matches with one character, i.e., 'A'. In this case, 'i' moves ahead and points to B and 'j' would be at the same location pointing to '*'.

Second case: '*' matches with no character. In this case, 'i' would remain at the same location and 'j' moves ahead and points to A character.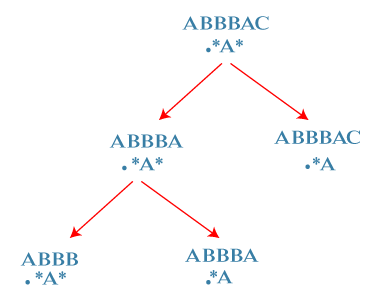

Now we will solve the right sub-tree.

Both 'A' in R and S are matched so 'A' will be removed from both R and S shown as below: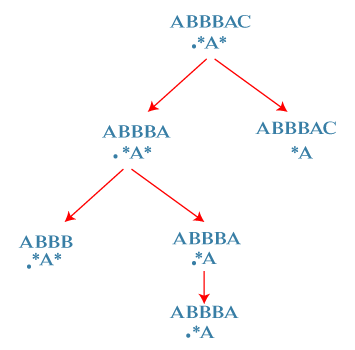

Again, there are two cases:

S = ABBB

R = .*

First case: '*' matches with one character, i.e., B. In this case, 'i' moves ahead and points to B and 'j' would be at the same location pointing to '*'.

Second case: '*' matches with no character. In this case, 'i' would remain at the same location and we move 'j' to the left.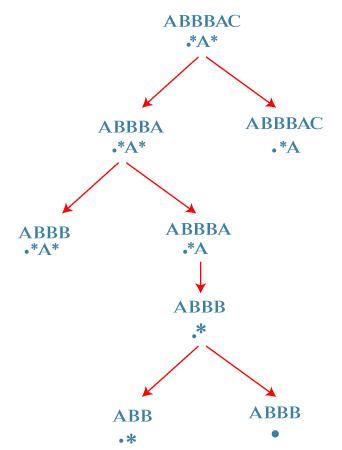

The next state is:

S = ABB

R = .*

First state: '*' matches with one character, i.e., B. In this case, 'i' moves ahead and points to B and 'j' would be at the same location pointing to '*'.

Second state: '*' matches with no character. In this case, 'i' would remain at the same location and we move 'j' to the left of '*'.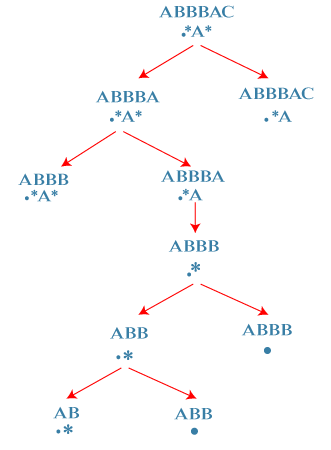

When we consider the right subtree where,

S = ABBB

R = .

When we match the regular expression with a string then '.' is matched with a 'B' character. It means that '.' character is removed from the regular expression and it becomes empty. The 'B' character is removed from the string S and it becomes "ABB". Since regular expression 'R' is empty but string 'S' is not empty so it returns false.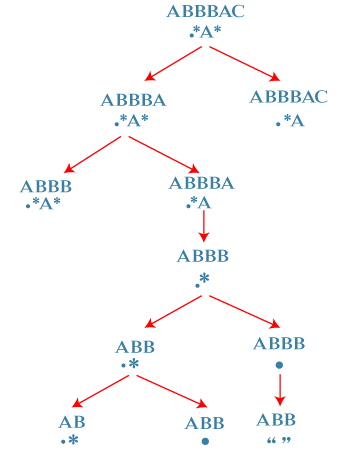

Now we consider another state where,

S = AB

R = .*

First state: '*' matches with one character, i.e., B. In this case, 'i' moves ahead and points to a and 'j' would be at the same location pointing to '*'.

Second state: '*' matches with no character. In this case, 'i' would remain at the same location and we move 'j' to the left of '*' pointing to '.' character.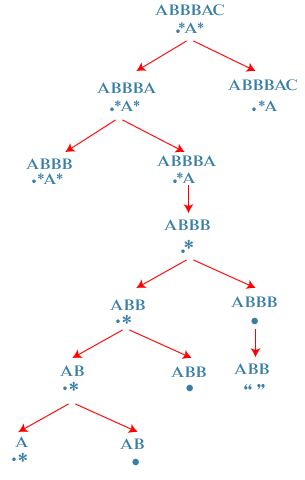

Now we consider another state where,

S = ABB

R = .

When we match the regular expression with a string then '.' is matched with a 'B' character. It means that '.' character is removed from the regular expression and it becomes empty. The 'B' character is removed from the string S and it becomes "AB". Since regular expression 'R' is empty but string 'S' is not empty so it returns false.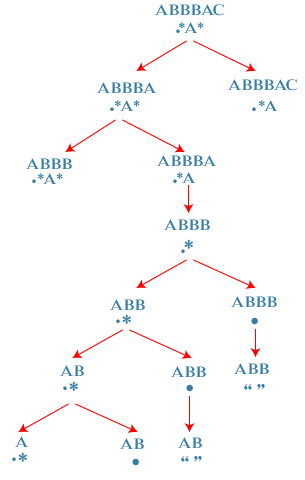

Now we consider another state where,

S = A

R = .*

First state: '*' matches with one character, i.e., A. In this case, string 'S' would become empty and 'j' would be remained at the same location pointing to '*' character. Since the string S is empty but regular expression 'R' is not empty so it returns false.

Second state: '*' matches with no character. In this case, 'i' would remain at the same location and we move 'j' to the left of '*' pointing to '.' character.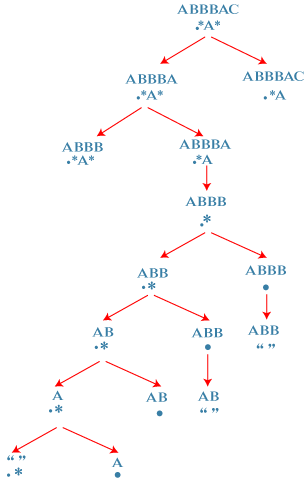

Now, we consider another state where,

S = A

R = .

Since the character '.' in R matches with 'A' in string 'S', so returns true. Now we have reached the base case where both the strings are empty and return true. Once we return true, it propagates all through to its top and return value of entire solution will be true. It means that string matches the regular expression.

3. Transitions

Base cases

i = 1 and j = -1, return true, all the characters matched and both S and R are empty.

i>=0 and j= -1, return false, some characters in S are unmatched.

i = -1 and j>= 0, return false, some characters in R are unmatched.

R[0: j] = '*', return true, * matches everything in S.

The following are the cases:

Case 1:

R[j] = S[i], then

matches(i, j) = matches(i-1, j-1)

Case 2:

R[j] = '.'

matches(i, j) = matches(i-1, j-1)

Case 3:

R[j] = '*'

If it matches with one character then,

matches(i, j) = matches(i-1, j)

If it matches with no character then,

matches(i, j) = matches(i, j-1 )

In the above two scenarios, the either of the functions return true then the output would be true.

Recurrence relation

matches(i, j, S, R) =True, if i = -1 and j = -1 // It means that both S and R are empty.

matches(i, j, S, R) = False, if i = -1 or j = -1 // It means that both S and R are not empty.

matches(i, j, S, R) = matches(i-1, j-1); if S[i] = R[j]

matches(i, j, S, R) = matches(i-1, j-1); if R[j] = .

matches(i, j) = matches(i-1, j) or matches(i, j-1 ), if R[j] = *

Let's see how can we implement the function matches()

4. Memoization

Now we will see how can we use the memorization or top-down approach to implement the dynamic programming.

We will use the 2d array to cache or store the results. Here we use i, j as a key or parameters.

It will return true if the string S[0 : i] matches with a regular expression R[0 : j]. We will cache the true value if the substring indexes at i matches with a regular expression index at j.

5. Bottom-up approach

Till now, we have seen the top-down approach. Now we will see that how can we implement the bottom-up approach using dynamic programming.

Recurrence relation

matches(i, j, S, R) = true, if i = -1, j = -1

matches(i, j, S, R) = false, if i = -1, j = -1

matches(i, j, S, R) = matches(i-1, j-1), if S[i] = R[j]

matches(i, j, S, R) = matches(i-1, j-1), if R[j] = .

matches(i, j, S, R) = matches(i-1, j) or matches(i, j-1), if R[j] = *

Bottom-up equation

Dp[i][j] = true, if i = 0, j=0

Dp[i][j] = false, if i = 0 or j = 0

Dp[i][j] = dp[i-1][j-1], if S[i-1] = R[j-1]

Dp[i][j] = dp[i-1][j-1], if R[j-1] = .

Dp[i][j] = dp[i-1][j] or dp[i][j-1] if R[j-1] = *

Let's implement the regular expression matching.