Methods of Minimum Spanning TreeThere are two methods to find Minimum Spanning Tree
Kruskal's Algorithm:An algorithm to construct a Minimum Spanning Tree for a connected weighted graph. It is a Greedy Algorithm. The Greedy Choice is to put the smallest weight edge that does not because a cycle in the MST constructed so far. If the graph is not linked, then it finds a Minimum Spanning Tree. Steps for finding MST using Kruskal's Algorithm:
MST- KRUSKAL (G, w)
1. A ← ∅
2. for each vertex v ∈ V [G]
3. do MAKE - SET (v)
4. sort the edges of E into non decreasing order by weight w
5. for each edge (u, v) ∈ E, taken in non decreasing order by weight
6. do if FIND-SET (μ) ≠ if FIND-SET (v)
7. then A ← A ∪ {(u, v)}
8. UNION (u, v)
9. return A
Analysis: Where E is the number of edges in the graph and V is the number of vertices, Kruskal's Algorithm can be shown to run in O (E log E) time, or simply, O (E log V) time, all with simple data structures. These running times are equivalent because:
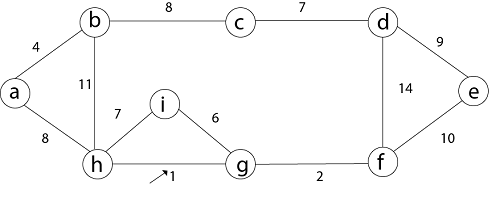
Thus the total time is For Example: Find the Minimum Spanning Tree of the following graph using Kruskal's algorithm. 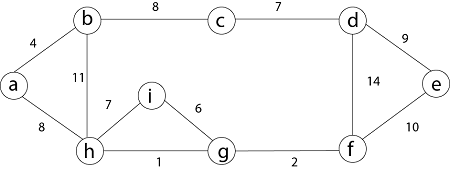
Solution: First we initialize the set A to the empty set and create |v| trees, one containing each vertex with MAKE-SET procedure. Then sort the edges in E into order by non-decreasing weight. There are 9 vertices and 12 edges. So MST formed (9-1) = 8 edges 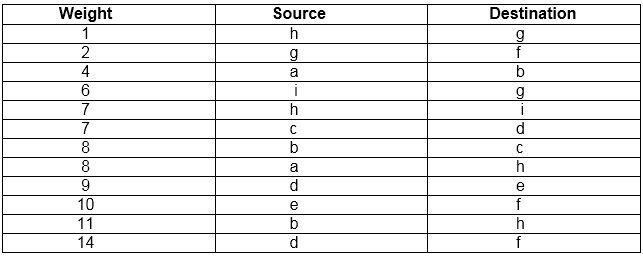
Now, check for each edge (u, v) whether the endpoints u and v belong to the same tree. If they do then the edge (u, v) cannot be supplementary. Otherwise, the two vertices belong to different trees, and the edge (u, v) is added to A, and the vertices in two trees are merged in by union procedure. Step1: So, first take (h, g) edge
Step 2: then (g, f) edge. 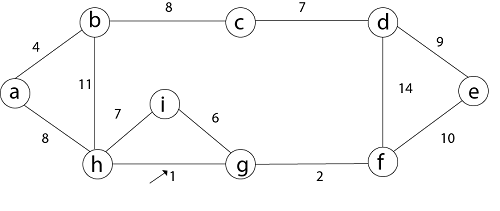
Step 3: then (a, b) and (i, g) edges are considered, and the forest becomes 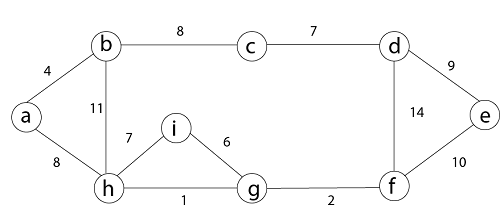
Step 4: Now, edge (h, i). Both h and i vertices are in the same set. Thus it creates a cycle. So this edge is discarded. Then edge (c, d), (b, c), (a, h), (d, e), (e, f) are considered, and the forest becomes. 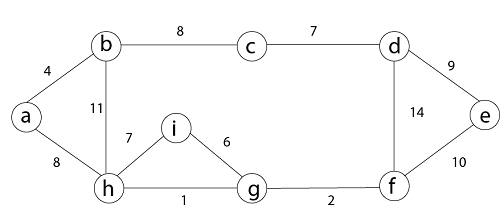
Step 5: In (e, f) edge both endpoints e and f exist in the same tree so discarded this edge. Then (b, h) edge, it also creates a cycle. Step 6: After that edge (d, f) and the final spanning tree is shown as in dark lines. 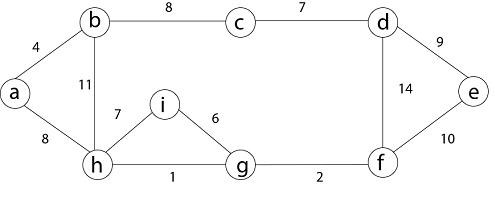
Step 7: This step will be required Minimum Spanning Tree because it contains all the 9 vertices and (9 - 1) = 8 edges 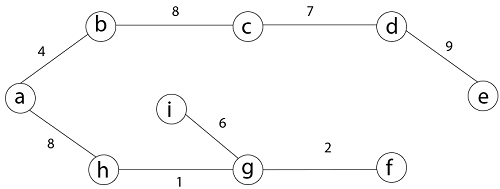
Minimum Cost MST
Next TopicPrim's Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share